Matykání: tajemný svět prvočísel
V roce 1900 předložil německý matematik David Hilbert svým kolegům 23 pečlivě vybraných problémů, ve kterých nastínil nejdůležitější směry budoucího vývoje matematiky. To, že dnes je většina z těchto problémů více méně vyřešena dokládá bouřlivý rozvoj královny věd v uplynulém století. Existuje však jedna oblast, která jako by zamrzla v čase. A netýká se nějakých esoterických vymyšleností. Naopak, dotýká se objektů, které si většina z nás pamatuje ze základní školy: prvočísel.
Jen několik let po Hilbertovi, v roce 1912, vyjmenoval jiný německý matematik Edmund Landau čtyři problémy dotýkající se právě prvočísel a v ostrém protikladu k Hilbertovým problémům není k dnešnímu dni vyřešen ani jeden z nich. Slovy: žádný. Ironické na tom je, že zatímco Hilbertovy problémy jsou technicky komplikované a pochopit, co se po vás vlastně chce vyžaduje poměrně hlubokou znalost vyšší matematiky, problémy nastíněné Landauem jsou na první pohled zcela elementární a jejich zadání můžete bez obtíží vysvětlit průměrnému gymnazistovi. Přesto si s nimi lidstvo už více než sto let neví rady. A vlastně ještě déle. Některé se datují až ke starým Řekům.
Taháček: prvočíslo je číslo dělitelné pouze jedničkou a sebou samým. Příklady: 2, 3, 5, 7, 11, 13,... (a dál se koukněte na tuto tabulku a nebo ještě lépe na tento obrázek).
V dnešním Matykání se těm 4 Landauovým problémům podíváme hezky zblízka na zoubek. Jeden každý z nich představuje poměrně jednoduché a srozumitelné tvrzení týkající se prvočísel. Přestože empirická data jasně naznačují, že všechna tvrzení pravděpodobně platí, ani pro jedno se zatím nepodařilo najít solidní logický důkaz.
Každé sudé číslo větší než 2 se dá vyjádřit jako součet dvou prvočísel.
Poznámka: Všimněte si, že toto je podstatně silnější tvrzení než kdybychom řekli, že sudých čísel s takovým rozkladem je nekonečně mnoho (to samozřejmě platí také a můžete si to dokázat za domácí úkol - není to nijak obtížné). Goldbachova hypotéza však tvrdí podstatně víc - a to, že všechna sudá čísla se dají takto zapsat. Podívejme se nejdříve na pár příkladů (občas se takových rozkladů dá najít i víc).
S vyššími čísly rozkladů samozřejmě přibývá:
100 = 3+97 = 11+89 = 17+83 = 29+71 = 41+59 = 47+53
102 = 5+97 = 13+89 = 19+83 = 23+79 = 29+73 = 31+71 = 41+61 = 43+59
104 = 3+101 = 7+97 = 31+73 = 37+67 = 43+61
106 = 3+103 = 5+101 = 17+89 = 23+83 = 47+59 = 53+53
108 = 5+103 = 7+101 = 11+97 = 19+89 = 29+79 = 37+71 = 41+67 = 47+61
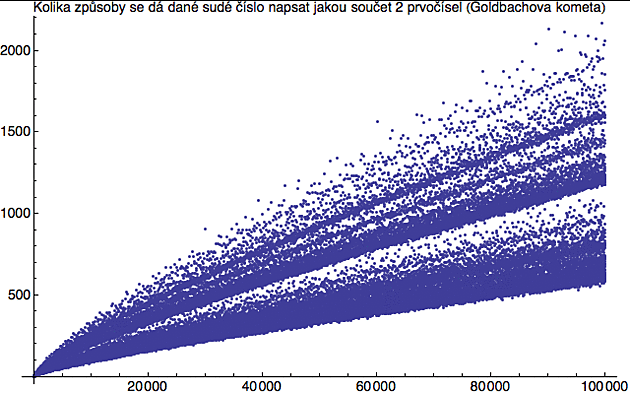
Ještě lépe je to vidět graficky. Na následujícím obrázku si pro každé sudé číslo (na ose x) vyneseme (na osu y) kolik prvočíselných rozkladů se dá najít. Z předchozí tabulky například vidíme, že pro 26 se takové rozklady dají najít 3 a proto do grafu v tomto případě zaneseme bod se souřadnicemi (26,3). A podobně pro ostatní sudá čísla. Protože už z tabulky vidíte, že počet rozkladů se celkem chaoticky mění, nedostaneme spojitou křivku, ale zvláštní graf, kterému se říká Goldbachova kometa.
Z tohoto grafu vidíte, že jakmile sudé číslo překročí 100000, těch rozkladů se dá najít řádově kolem 500. Přesto stále neumíme dokázat, že pro každé sudé číslo existuje alespoň jeden jediný (!). Důvodem je příslovečná vrtošivost prvočísel.
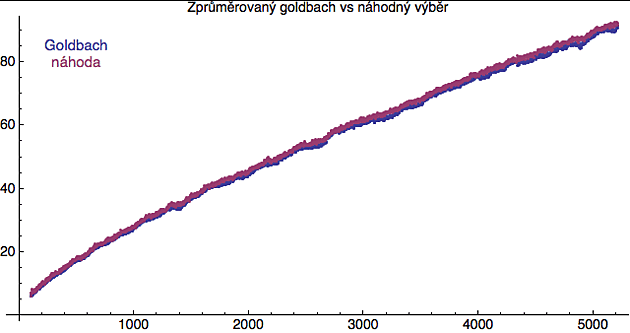
Přestože jsou definováná zcela přesně a rigorózně, prvočísla se v mnoha ohledech chovají jako náhodná čísla. Na dalším obrázku uvidíte malý pokus, kdy jsem si pro dané sudé číslo místo prvočísel vzal náhodně vybraná lichá čísla (tak aby jejich počet odpovídal počtu skutečných prvočísel) a pak jsem si položil otázku kolika způsoby se dá to sudé číslo vyjádřit jako součet těchto "fejkových" prvočísel. A protože náhodný výběr se dá zopakovat, udělal jsem to pro každé sudé číslo 500x. Výsledný průměrný počet (červená křívka) jsem pak porovnal se zprůměrovanou verzí skutečné Goldbachovy komety - tedy pro každé sudé číslo jsem vzal průměr počtu prvočíselných rozkladů pro 10 předcházejících a 10 následujících sudých čísel (modrá křivka). Vidíte že chování skutečných prvočísel a náhodně vybraných lichých čísel se prakticky neliší (jedna křivka překrývá druhou).
2. Hypotéza prvočíselných dvojčat
Existuje nekonečně mnoho prvočíselných dvojčat.
Poznámka: Prvočíselná dvojčata jsou dvě prvočísla mezi kterými je rozdíl 2 (například 41 a 43). To je v podstatě nejmenší možný rozdíl - jediná prvočísla, která následují hned po sobě jsou 2 a 3.
Mezi prvními 11 prvočísly (2,3,5,7,11,13,17,19,23,29,31) je dvojčat celkem 5 (zkuste si je najít). To je zhruba 45%. Jak ale začnete zkoumat víc a víc prvočísel, procentuální podíl dvojčat klesá. Opět se na to podíváme graficky. Na ose x nanesu kolik prvočísel budu uvažovat a na ose y pak uvidíme kolik procent z nich jsou dvojčata (tedy přesněji, kolik procent z těch prvočísel p má tu vlastnost, že p-2 je taky prvočíslo). Vidíte, že procento poměrně rychle klesne na hodnotu 10% a pak velmi pomalu klesá dál.
Tahle hypotéza v podstatě říká, že existuje nekonečně mnoho prvočíselných dvojic, jejichž vzdálenost na číselné ose je přesně 2. V roce 2013 vzbudil velký rozruch do té doby neznámý čínský matematik Yitang Zhang, který dokázal podstatně slabší variantu a totiž, že existuje nekonečně mnoho prvočíselných dvojic, které jsou od sebe vzdáleny maximálně 70 miliónů. Velikost tohoto čísla sama o sobě Vám poskytuje obrázek, jak těžké je cokoliv o prvočíslech dokázat. Od té doby se na jeho důkaz dychtivě vrhla celá smečka matematiků a postupně se jim podařilo tu vzdálenost zredukovat až na 246 - to je ale stále daleko od konečného cíle 2 (tedy tolik, kolik dělí prvočíselná dvojčata).
Mezi dvěma po sobě jdoucími čtverci vždy existuje prvočíslo.
Poznámka: dvěma po sobě jdoucími čtverci se základnou N rozumím dvojici N2 a (N+1)2
Česky se to dá říci takto - představte si posloupnost čtverců: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121... Legendrova domněnka říká, že mezi každými dvěma čísly této posloupnosti najdete alespoň jedno prvočíslo. Pokud si vezmeme základnu třeba 7, tak ty dva po sobě jdoucí čtverce jsou 49 a 64 a mezi nimi existuje ne jedno, ale hned tři prvočísla: 53, 59 a 61. Zda to tak ale funguje až do nekonečna nevíme.
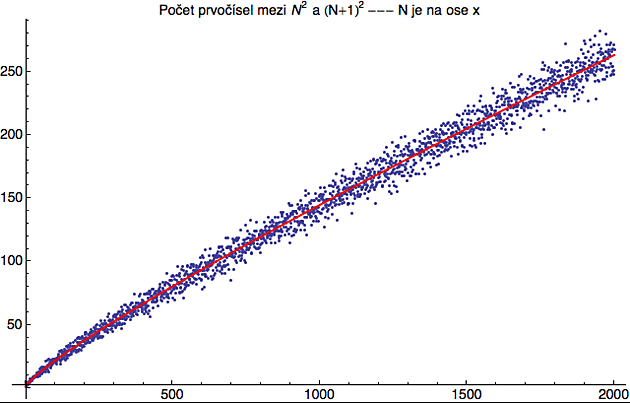
Samozřejmě pro vyšší hodnoty základny jsou mezery mezi čtverci větší a větší a vejde se do nich prvočísel daleko víc (prvočísel sice obecně ubývá, ale zvětšování mezer mezi čtverci tento proces více než kompenzuje). Podívejme se na to nejprve graficky. Na ose x nanesu základnu N a na ose y uvidíme počet prvočísel mezi N2 a (N+1)2.
Zajímavé je, že ze znalosti statistiky prvočísel umíme (*) poměrně přesně odhadnout kolik těch prvočísel mezi danými čtverci bude. Vzdálenost mezi čtverci o základně N je 2N+1 a protože hustota prvočísel kolem čísla N je přibližně 1 / ln(N) můžeme očekávat zhruba N / ln(N) prvočísel. To je ta červená křivka a vidíte, že v průměru funguje docela přesně. I proto si myslím, že z Landauových problémů je tento asi nejschůdnější.
(*) pokud je vám divné, že ovládáme statistiku prvočísel, ale jejich individuální vlastnosti nám dělají těžkosti, představte si třeba předvolební preference ANO. To, že známe poměrně přesně procentuální zastoupení jejich příznivců v populaci ještě neznamená, že když čapneme náhodného chodce na ulici, budeme schopni odhadnout, zda je to volič ANO nebo ne. A s prvočísly je to podobně.
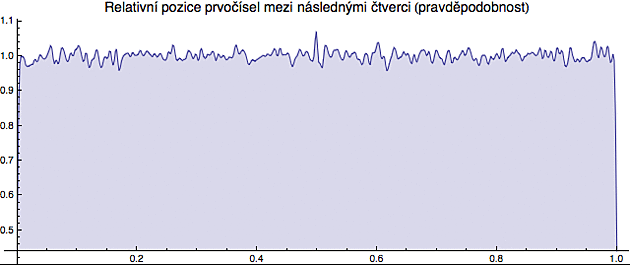
Na závěr se podívejme, kde mezi danými čtverci se ta prvočísla většinou nalézají. Za tím účelem si pozici mezi 2 následnými čtverci převedu na bezrozměrné jednotky j z intervalu (0,1) a pro prvních 2000 dvojic čtverců najdu všechna prvočísla mezi nimi a vynesu si do grafu, kde se nacházejí (ve formě hustoty pravděpodobnosti veličiny j - tedy v podstatě spojitého histogramu).
Pokud Vás ty bezroměrné jednotky zajímají, tak pro dva následné čtverce A a B a pro prvočíslo p mezi nimi jsou definovány takto: j = (p-A)/(B-A). Takže pozice prvočísla 41, které leží mezi čtverci 36 a 49, odpovídá bezrozměrné jednotce j = 0,3846.
Hodnota 0 tedy odpovídá prvnímu čtverci, hodnota 1 druhému - v nich samozřejmě prvočíslo být nemůže, proto je tam pravděpodobnost výskytu nula.
Jak vidíte, prvočísla jsou mezi čtverci rozložena naprosto rovnoměrně. Žádná pozice není zvýhodněna. I to svědčí o tom, že se chovají tak trochu jako náhodná čísla. Ale ne úplně. Podívejte se třeba na útvar zvaný Ulamova spirála. Něco takového byste z úplně náhodných čísel nevytloukli.
4. Prvočísla v kvadratických posloupnostech
Existuje nekonečně mnoho prvočísel tvaru n2+1
Poznámka: Toto je speciální případ Bunyakovského domněnky, která se zabývá výskytem prvočísel v polynomiálních posloupnostech.
Jen co lidstvo - prostřednictvím starořeckých matematiků - zjistilo, že posloupnost přirozených čísel obsahuje nekonečně mnoho prvočísel, začalo hloubat, které podposloupnosti mají tutéž vlastnost. První padly pochopitelně na řadu aritmetické posloupnosti, které se dají zapsat jednoduchou lineární formulkou a+d*n, kde a a d jsou dvě nesoudělná čísla (a za n si postupně dosadíte všechna přirozená čísla). Jako příklad si můžete zkusit formulku 2+7*n, ze které po dosazení přirozených čísel vyždímáte následující posloupnost: 9, 16, 23, 30, 37, 44, 51, 58, 65, 72, 79 ...
Taháček: dvě čísla jsou nesoudělná pokud nemají společného dělitele (např. 2 a 7).
Už od pohledu je jasné, že nějaká prvočísla ta posloupnost opravdu obsahuje, ale zda je jich nekonečně mnoho se nedá jen tak lehce posoudit. Tento problém vzdoroval úsilí mudrlantů více než dva tisíce let a teprve v roce 1837 německý matematik Dirichlet dokázal, že za podmínky nesoudělnosti a a d obsahují všechny lineární (aritmetické) posloupnosti a+d*n nekonečně mnoho prvočísel. Jeho důkaz však používá poměrně komplikovaný matematický aparát a pro blog se nehodí.
Jako další přišly samozřejmě na řadu posloupnosti kvadratické a z nich nejjednodušší je právě n2+1. Když si napíšete prvních několik členů (tedy dosadíte za n postupně 1, 2, 3,..), dostanete:
2, 5, 10, 17, 26, 37, 50, 65, 82, 101, 122, 145, 170, 197, ....
I zde je od pohledu jasné, že nějaká ta prvočísla se v této posloupnosti skutečně nalézají, ale zda je jich nekonečně mnoho nevíme dodnes (to je právě obsahem 4. Landauova problému!). Protože za n dosazujeme přirozená čísla, je celkem jasné, že pro lichá n bude výraz n2+1 sudý a tudíž (s výjimkou n=1) nemá šanci být prvočíslem. Proto stačí omezit se při bádání na sudé hodnoty n. Můžete si sami zkusit, že prvních pár sudých čísel n pro které naše formulka vyplivne prvočíslo je:
2, 4, 6, 10, 14, 16, 20, 24, 26, 36, 40, 54, 56,...
(této posloupnosti budu říkat "červená posloupnost" - za chvíli uvidíte proč)
Abyste si udělali obrázek, jak těžký tento problém je, poznamenám, že zatím nejlepšího výsledku dosáhl v roce 1978 polský matematik Henryk Iwaniec, který ukázal, že posloupnost n2+1 obsahuje nekonečně mnoho čísel, která jsou buď prvočísla a nebo mají jen dva prvočinitele (rozmyslete si, že toto je o něco slabší tvrzení než 4. Landauův problém). Profesora Iwaniece jsem jednou v 90. letech potkal na konferenci v New Yorku a když jsem mu řekl, že mě ten problém docela zajímá, dal mi důrazné varování: "Nemarněte svůj čas, mladý muži". Takže než se pustíte do jeho řešení, dobře si rozvažte, jestli by nebylo vhodnější raději na zahradě okopávat okurky.
Závěrem se podívejme na jednu zajímavou geometrickou interpretaci 4. problému. Představte si, že budete kreslit kružnice se středem v počátku a to tak aby procházely bodem o souřadnicích (n,1), kde n je sudé přirozené číslo - takovým budu říkat sudé body. Na obrázku níže vidíte kružnice procházející sudými body (2,1), (4,1), (6,1),... atd až (60,1). To je ta spodní řada bodíků.
Všimněte si, že občas se stane, že taková kružnice protne ještě jiný bod s celočíselnými souřadnicemi - tedy průsečíky té mřížky (aby to bylo lépe vidět, nakreslil jsem to na milimetrovém papíře). Například kružnice procházející sudým bodem (8,1) prochází také bodem (4,7). A samozřejmě také symetrickými body (1,8) a (7,4). Nebo kružnice skrz bod (22,1) prochází také bodem (14,17). Ale ne vždy se to podaří. Třeba kružnice procházející bodem (10,1) už žádný jiný celočíselný bod mřížky neprotne - kromě triviálního (1,10) samozřejmě. Ty kružnice, které ještě nějaký další celočíselný (mřížkový) bod protnou jsem obarvil modře (a průsečík jsem zvýraznil) a ty zbylé červeně.
A teď si z obrázku odečteme, jakými sudými body ty červené kružnice procházejí: 2, 4, 6, 10, 14, 16, 20, 24, 26, 36, 40, 54, 56... To je ale náhodička! To je přesně ta červená posloupnost výše. Jinými slovy, toto jsou přesně ta sudá čísla, pro která nám formulka n2+1 vytvoří prvočíslo (až se dostaneme ke komplexním číslům, tak se k této zajímavosti vrátím).
Ten 4. problém tedy můžeme přeformulovat takto. Mezi všemi kružnicemi, procházejícími těmi sudými bodíky na spodní řadě, existuje nekonečně mnoho takových, které už žádné jiné mřížkové body neprotnou. Jinými slovy, pokud bychom ten obrázek prodloužili doprava, tak bychom měli vidět nekonečně mnoho červených kružnic. Jenže zatím nikdo nedokázal, že tomu tak skutečně bude.
My - jako lidstvo - sice umíme rozštěpit atom a své bližní poslat na Měsíc, ale o vlastnostech prvočísel toho pořád moc nevíme.
A na uklidněnou si dnes dovolím ještě jednou pozvat do vašich počítačů Petulu Clark. Pokud je mi známo, její písnička "A Sign of the Times" nemá česky nazpívanou verzi (jako třeba minule vzpomenutý Downtown), ale přesto doufám, že těm, kdo se prokousali celým článkem až sem trochu spraví náladu. Pokud chcete vidět zpěvačku přímo v akci, jukněte sem (video je sice trochu poškozené, ale zvuk je v pohodě).
Předchozí díly Matykání
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
| Další články autora |
Tři roky vězení. Soud Ferimu potvrdil trest za znásilnění, odvolání zamítl
Městský soud v Praze potvrdil tříletý trest bývalému poslanci Dominiku Ferimu. Za znásilnění a...
Moderní lichváři připravují o bydlení dlužníky i jejich příbuzné. Trik je snadný
Premium Potřebujete rychle peníze, pár set tisíc korun a ta nabídka zní lákavě: do 24 hodin máte peníze na...
Takhle se mě dotýkal jen gynekolog. Fanynky PSG si stěžují na obtěžování
Mnoho žen si po úterním fotbalovém utkání mezi PSG a Barcelonou postěžovalo na obtěžování ze strany...
Školu neznaly, myly se v potoce. Živořící děti v Hluboké vysvobodili až strážníci
Otřesný případ odhalili strážníci z Hluboké nad Vltavou na Českobudějovicku. Při jedné z kontrol...
Prezident Petr Pavel se zranil v obličeji při střelbě ve zbrojovce
Prezident Petr Pavel se při střelbě na střelnici v uherskobrodské České zbrojovce, kam zavítal...
Ukrajinci v branném věku budou moci získat pas jen ve vlasti, rozhodl Kyjev
Ukrajinská vláda přijala rozhodnutí, podle něhož muži ve věku od 18 do 60 let budou moci získat...
Biskupové se distancovali od Zemanovy akce v Arcibiskupském paláci
Pražský arcibiskup Jan Graubner se distancoval od akce, při které byla minulý týden v...
Pokleknete a budete prosit. Generál slíbil zničit NATO do roku 2030
Velitel čečenských sil bojujících na Ukrajině a věrný obdivovatel ruského prezidenta Vladimira...
Maďarský zákon o svrchovanosti dráždí europoslance, mají „vážné obavy“
Nový maďarský zákon o svrchovanosti, který má bránit zásahům zvenčí do národní politiky, v rezoluci...

Akční letáky
Prohlédněte si akční letáky všech obchodů hezky na jednom místě!
- Počet článků 402
- Celková karma 19,54
- Průměrná čtenost 920x