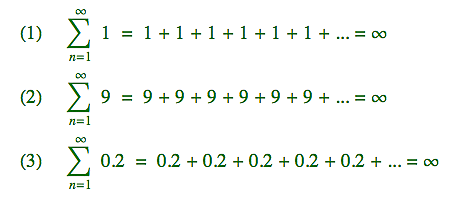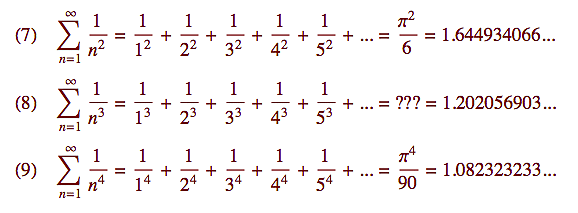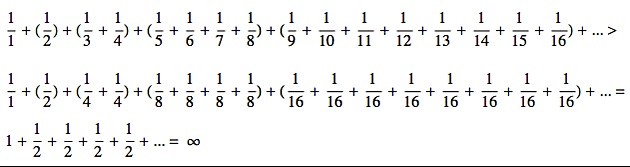Matykání: na konečné nekonečné řady

Dnes budeme počítat, až se z nás bude kouřit. Moc velká sranda to nebude. I nějaké ty vzorečky budou létat vzduchem. Komu se dělá v ostřelované tramvaji nevolno, má poslední šanci vystoupit.

Zatím jsme nekonečno jen tak opatrně zdálky okukovali. Dnes se v něm hezky vyválíme. A nejlepším bahništěm pro takové špásování jsou nekonečné řady. Přesněji nekonečné řady čísel, jejichž celkový součet se snažíme zjistit. Začneme s těmi nejjednoduššími - tedy s konstantními.

V jednom z předchozích matykání jsme se do nekonečna proplížili usilovným počítáním nekonečného stáda oveček: první, druhá, třetí, čtvrtá a tak dále - až jsme se dopočítali (tedy ti z nás kdo neusnuli) až do aleluja. Technicky vzato jsme vlastně sečetli nekonečně mnoho jedniček. Výsledku takového procesu se říká nekonečný součet (nebo přesněji součet nekonečné řady) a když si ho zapíšeme za pomoci rovnítek, tak vypadá zhruba takto - viz (1):

Samozřejmě můžeme sčítat i kladná čísla, která jsou větší (2) a nebo menší (3) než jedna, ale za předpokladu, že se ta sčítaná čísla nemění, tak se k nekonečnu dříve nebo později vždy propracujeme.

Ten první výraz (obsahující řecké písmenko sigma) není nic jiného než schematický zápis dané řady, ve kterém uvedeme jaký výraz sčítáme (ten výraz může záviset na n - viz níže) a pod sigma a nad sigma vyznačíme pro jaké hodnoty n ho hodláme sčítat - tedy odkud kam. Druhý výraz je rozvinutý zápis dané řady, ve kterém ty tři tečky znamenají, že v daném trendu pokračujeme až do nekonečna. Tento výraz by měl být srozumitelný většině smrtelníků. A konečně úplně vpravo je finální součet.

Geometrické řady

Konstantní řady jsou samozřejmě trochu jednotvárné. Podstatně větší zábava nastane, když začnete sčítat čísla, která se zmenšují. V takových případech můžete někdy i po nekonečně mnoha krocích dostat konečný součet a asi nejjednodušším příkladem tohoto jevu jsou tzv. geometrické řady, které si možná pamatujete ze střední školy: a+aq+aq2+aq3+.... Ten podivný výraz znamená, že začneme s nějakým číslem a a následující člen získáme vždy tak, že předchozí člen vynásobíme určitou konstantou q - té se říká kvocient řady. V následujících ukázkách je ten kvocient 1/2, 1/3 a 1/4 (navíc se zde první člen a kvocient náhodou rovnají - i když obecně to mohou být různá čísla).

Podívejme se nejprve podrobněji na první geometrickou řadu, označenou číslicí (4).

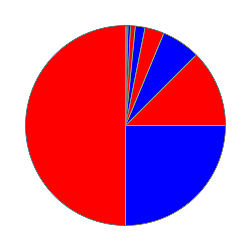
Abychom si udělali hrubou představu o tom, proč sečtením nekonečně mnoha čísel můžeme dostat konečný výsledek, zde konkretně 1, představme si sčítaná čísla jako plátky pizzy (červenomodré výseče na obrázku vlevo). Když si tu formulku (4) vyčíslíme, zjistíme, že sčítáme polovinu, plus čtvrtinu, plus osminu, plus šestnáctinu a tak dále. Důležité je všimnout si následující vlastnosti: v každém okamžiku příčítáme polovinu toho, co nám ještě zbývá do celé pizzy. Například v okamžiku, kdy jsme sečetli polovinu a čtvrtinu, tak nám k plné pizze zbývá čtvrtina a v dalším kroku skutečně přidáme polovinu toho co zbývá (tedy osminu). A když si tento postup v hlavě zacyklujete, tak se po nekonečně mnoha přidáních užších a užších plátků opravdu dopracujete k celé pizze. Ten magický okamžik na konečné, kdy budete mít na talíři kompletní pizzu, ale vyžaduje určitou představivost, protože provedení nekonečně mnoha operací (přičtení) je přece jenom trochu exotický myšlenkový proces.

Študáci na střední škole si s filosofickým podtextem nekonečného součtu většinou moc hlavu nelámou, protože na součet geometrické řady a+aq+aq2+aq3+... mají formulku, která říká, že její součet se rovná a/(1-q), kde q je kvocient a a její první člen. Takže je potřeba ze zápisu řady jen vykoumat hodnotu těchto parametrů a dosazením se pak získá číslo, které většinou odvrátí páně profesorovu zálibu v trápení žactva. Třeba řada (6) má první člen 1/4, kvocient také 1/4, takže její celkový součet je 1/3. To si můžete ověřit tak, že sečtete prvních řekněme sto členů a uvidíte, že výsledek se bude jedné třetině skutečně blížit.

Tento vzoreček není těžké si odvodit. Především vytknete ten první člen a a po zkrácení zjistíte, že stačí když ukážete, že 1+q+q2+q3+... = 1/(1-q). Ten výraz nalevo si označíme písmenkem S (tedy S =  1+q+q2+q3+... ) a když ho vynásobíme hodnotou q dostaneme: S*q = q+q2+q3+... Dále vidíme, že když výrazy pro S a S*q  odečteme, skoro všechno se vyruší, takže dostaneme S - S*q = 1 a odtud už je jednoduché spočítat, že S = 1/(1-q).

Teď se tomu vzorečku podíváme trochu pod kapotu, abychom viděli jak ta nekonečná suma vlastně funguje.

V tabulce napravo (ve sloupci označeném suma_1) jsem spočítal součet prvních n členů té první geometrické řady (4), kde n vidíte v levém sloupci (ten pravý sloupec zatím ignorujte). Můžete si to představit jako jízdu tramvají, kde v každé zastávce přičtete další člen. V první zastávce (n=1) máte na displeji kalkulačky 1/2, ve druhé 1/2 + 1/4, ve třetí 1/2 + 1/4 + 1/8, atd...

Všimněte si, že když sečtete prvních dvacet členů té řady, jste už prakticky v jedničce (tedy máte už skoro celou pizzu). Součet je v tomto okamžiku 0.999999. Ale ačkoliv těch devítek stále  přibývá, v žádné (konečné) zastávce tu jedničku neuvidíte, pouze se k ní více a více přibližujete. Teprve v okamžiku, kdy dojedete na konečnou té nekonečné řady, tedy do nekonečna, tak Vám na displeji ta jednička naskočí (já vím - v praxi vám tam naskočí dřív, protože kalkulačky zaokrouhlují, ale tím se v tuto chvíli nenechme rozhodit).

Ta jednička je vlastně tak trochu idealizovaná hodnota, která reprezentuje výsledek našeho sčítacího úsilí, pokud bysme byli schopni ho nekonečněkrát zopakovat. Této idealizované hodnotě (tedy součtu v zastávce nekonečno) se v matematice říká limita a na tomto pojmu je vpodstatě postaven celý diferenciální počet. Když si představíte neomezené pokračování toho prostředního sloupce (suma_1), tak jeho limita není žádná konkretní hodnota na nějakém konkretním řádku, ale to číslo ke kterému se pomalu ale jistě blížíme (v našem případě 1). To číslo samozřejmě nemusí vždy existovat - známe spoustu číselných řad, které prostě limitu nemají (např. 1-1+1-1+1-1+1-1+1...).

Řadám, které mají na té poslední zastávce konečný součet říkáme konvergentní. To, že řada konverguje tedy znamená, že zmíněná limita jednak existuje a jednak je konečná.

Riemannova zeta funkce

Když se podíváte na jmenovatele v těch geometrických řadách, vidíte, že jsme nějaké konkretní pevné číslo (zde 2, 3 a 4) umocňovali na vyšší a vyšší mocniny. Daleko zajímavější situace vznikne v obráceném gardu, tedy když budeme (opět ve jmenovateli) umocňovat stále vyšší a vyšší čísla na nějakou konkretní pevnou mocninu. Jinými slovy, když prohodíme základy a exponenty. Takto vzniklé řady (7) - (9) se používají například v definici jedné z nejdůležitějších funkcí současné matematiky - Riemannovy Zeta funkce, na kterou se podíváme někdy v budoucnosti. Zatím Vám prozradím jen to, že na zjištění přesné polohy nulových bodů této funkce (ty si můžete představit jako kořeny polynomu) je vypsána odměna milión dolarů.

První věc, kterou můžeme zaregistrovat je, že některé formulky pro finální součet obsahují řecké písmenko ? (pí). S ním se setkáváme většinou v geometrii při výpočtu obsahů a objemů kulatých těles. Jeho přítomnost ve vzorečku pro řady, které se sestávají z převrácených hodnot jakýchsi celočíselných mocnin naznačuje, že číslo ? (3.14159...) má v matematice daleko hlubší poslání než jenom asistovat při počítání s kulatinami. Všimněte si, že ta čísla, která sčítáme, nemají s žádnými kruhy nic společného.

Důkaz platnosti těchto vzorečků je podstatně komplikovanější než u geometrické řady, takže Vás téchto pekelných muk ušetřím.  Ale pokud Vás třeba zajímá, odkud se to ?2 v rovnici (7) vyloupne, můžete se podívat na 14 důkazů této formulky.

Druhá zajímavá věc je, že zatímco vzoreček pro ten součet se čtverci (7) byl znám už Eulerovi v 18. století a vzorečky pro další sudé mocniny (třeba ty čtvrté na řádku označeném (9)) známe minimálně od století devatenáctého, dodnes nikdo neví jaký je přesně součet těchto řad pro liché mocniny - jako například (8). Samozřejmě si ta čísla můžeme s libovolnou přesností vyčíslit, například tak, že ty řady prostě na počítači sečteme pro prvních řekněme trilion členů, ale přesný vzoreček, který by nám ty finální součty vyjádřil za pomoci známých matematických konstant a algebraických operací zatím neznáme.

Dokonce ani pořádně nevíme, zda jsou ty finální součty pro liché mocniny čísla racionální (zlomky) a nebo iracionální. Velkou senzaci proto v roce 1978 způsobil francouzský matematik Roger Apéry, který dokázal, že součet řady (8) je iracionální číslo. Jeho důkaz se však nepodařilo rozšířit na další liché mocniny, takže o iracionalitě součtu podobné řady řekněme s pátými nebo sedmými mocninami stále nic nevíme.

Harmonická řada

Možná teď máte pocit, že sčítání nekonečných řad je principielně snadná záležitost. Buďto jsou sčítaná čísla konstantní (jako příklady 1 až 3) a pak se dopočítáme k nekonečnu a nebo se ta čísla zmenšují k nule (jako v příkladech 4 až 9) a pak je jejich součtem nějaké konečné číslo. Skutečnost je bohužel složitější a to, že se sčítaná čísla stávají menšími a ještě menšími ještě nemusí být zárukou konečnosti výsledného součtu.

Nejznámějším příkladem je tzv. harmonická řada, což je vpodstatě součet převrácených hodnot přirozených čísel: 1/1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + ... Toto je mimochodem jediná z těch červených řad, kterou umíme sečíst, přestože je definována pomocí lichých mocnin (v tomto případě prvních). Její součet je totiž (trochu překvapivě) nekonečno, přestože se sčítaná čísla poctivě zmenšují k nule.

Důkaz tohoto faktu není těžký, ale než se na něj podíváme, ukážu vám jednu sčítací analogii z praktického života.

Představte si, že máte v kapse pětistovku a přijdete do obchodu, kde si chcete koupit čtyři věci, jejichž cena je 137 Kč, 236 Kč, 119 Kč a 109 Kč. Máte na to? Odpověď je - nemáte a není ani nutno ta 4 čísla pracně sčítat. Stačí totiž zaokrouhlit dolů na nejbližší stovky a teprve pak sečíst (což je samozřejmě podstatně jednodušší než sčítat původní ceny): 100 + 200 + 100 + 100 = 500. No a hned vidíte, že Vám prachy nevyjdou. I ta zmenšená čísla už dávají pětistovku, takže je jasné, že posčítáním původních cen (které jsou vyšší) se dostanete nad svoji momentální hotovost.

Důkaz toho, že harmonická řada má nekonečný součet probíhá podobně. Nejprve nahradíme čísla v té řadě čísly, která jsou sice o něco menší, ale dají se snadněji posčítat. No a pak ukážeme, že i tato menší čísla už dají nekonečno. Tím pádem původní harmonická řada, jejíž členy (a tedy i součet) jsou o něco větší musí mít také nekonečný součet, protože cokoliv větší než nekonečno musí být také nekonečno.

Takže s chutí do toho.

Nejprve si harmonickou řadu nasekáme na zvětšující se oddíly, které pro přehlednost umístíme do závorek. Konkretně: jedničku vynecháme a ten zbytek uzavřeme do chlívků, v nichž bude počet členů odpovídat mocninám dvojky. Tedy první chlívek bude mít jeden člen, druhý dva, ten další čtyři, následující osm, a pak 16, 32, 64, 128, ... a tak dále.

Potom v každém chlívku (závorce) nahradíme všechna čísla číslem posledním, čímž součet v závorce trochu zmenšíme (tento krok odpovídá zaokrouhlení na stovky z předchozího příkladu). Rozmyslete si, že ten poslední člen je skutečně menší než všechny členy před tím, takže součet skutečně zmenšujeme, jak je níže naznačeno použitím symbolu pro nerovnost ">". A pak už si jen uvědomíme, že součet všech těch zmenšených členů v každé závorce je 1/2, takže vlastně sčítáme jedničku plus nekonečně mnoho polovin a to je samozřejmě rovno nekonečnu.

Tady je to zapsáno ve formulce:

Pokud se ještě jednou podíváte na tu tabulku pod červenomodrou pizzou (sloupeček suma_2), najdete v ní i součty prvních n členů harmonické řady. Vidíte, že její součty rostou rychleji než řada geometrická (což byl sloupeček suma_1), ale ten růst se stále zpomaluje, takže není apriori jasné, zda se ta nekonečná řada k nekonečnu nakonec doplazí a nebo zda uvízne na nějakém konečném čísle. Na prokázání nekonečnosti jejího součtu je právě potřeba narafičit výše popsaný mechanismus.

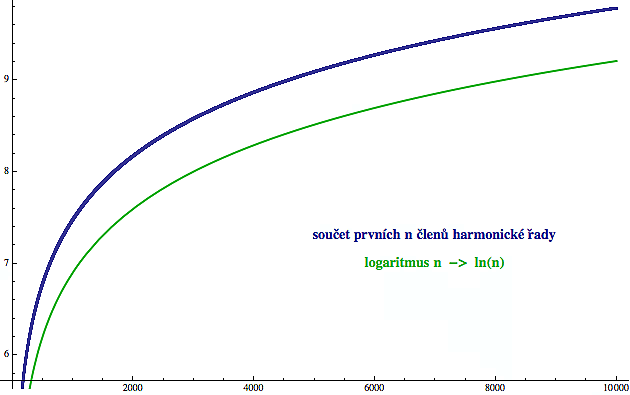
Ještě lépe je ten zpomalující se růst vidět, pokud si nakreslíme graf. Na ose x je vyneseno n a na ose y vidíme součet prvních n členů harmonické řady (to je v podstatě rozšířený sloupek suma_2). Pokud Vám ta modrá křivka připomíná logaritmus, nejste daleko od pravdy (souvisí to s tím, že integrál 1/x je ln(x)). Proto jsem pro srovnání do grafu zanesl i přirozený logaritmus n (zeleně).

Skoro by se zdálo, že stačí ten logaritmus trochu "šoupnout nahoru" a ty dvě křivky by se víceméně překrývaly. To je pravda v následujícím smyslu. Pokud si pro každé n zaznamenáte o kolik se ty dvě křivky liší, zjistíte, že pro hodně velká n se to "šoupnutí" blíží hodnotě 0,57721 56649 01532 86060 65120 90082 40243 10421... (ano, je to tedy určitý typ limity). Tomuto číslu se říká Eulerova konstanta a v matematice, zejména v teorii čísel, hraje poměrně významnou roli - i když není ani zdaleka tak populární jako třeba čísla e nebo ?. Ovšem zatímco u obou posledně zmíněných je už delší dobu známo, že se jedná o čísla iracionální (tedy nejsou to zlomky), u Eulerovy konstanty to stále nevíme, takže pokud se chcete před celým světem matematicky blýsknout, můžete dokázat, že to dlouhé desetinné číslo se nedá vyjádřit jako zlomek. Ale milión doláčů za to asi nebude...

Tak hodně štěstí.

A na uklidněnou si dáme do třetice Petulu Clark. Tentokrát v písničce Winchester Cathedral, kterou u nás proslavil Václav Neckář pod názvem Chrám svatého Víta.

Předchozí díly Matykání