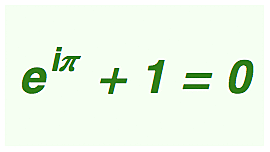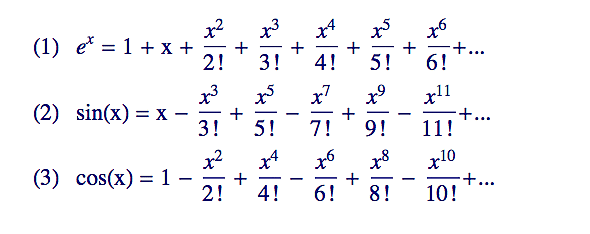Matykání: nejkrásnější rovnice světa
V roce 1988 uspořádal popularizační časopis Mathematical Intelligencer mezi svými čtenáři anketu o nejkrásnější rovnici světa. Přesvědčivě v ní zvítězila tzv. Eulerova identita, úhledná rovnice svazující pět základních matematických konstant (0,1,i,e,?) prostřednictvím překvapivě jednoduchého vztahu (viz obrázek vpravo). Její pozici světové jedničky mezi rovnicemi, tedy jakési pomyslné Miss Equation, potvrdil i nedávný článek BBC, který na Eulerově mistrovském kousku oceňuje sloučení zdánlivě nesouvisejících čísel v jeden hutný a koncizní celek.
Leonardo da Vinci kdysi řekl, že "jednoduchost je nejvyšší formou sofistikovanosti". Elegance, s kterou tato rovnice spojuje obě mystické konstanty e a ?, jí přisuzuje kultovní status mezi příznivci královny věd (postavení Eulerovy identity není zcela nepodobné roli, kterou hraje Einsteinova rovnice E=mc2 ve fyzice - i když její popularity zdaleka nedosahuje).
V dnešním Matykání se podíváme, odkud se tato rovnice vzala a jaké jsou její důsledky.
(z typografických důvodů ji budu zapisovat jako: exp(i?)+1=0)
+++++++++
Komplexní funkce
Komplexní funkci si - stejně jako její reálný protějšek - můžeme představovat jako skříňku s trpaslíkem. Vhodíte do ní komplexní číslo, trpaslík s ním podle přesně definovaného algoritmu provede určitou operaci - aritmetickou, geometrickou nebo jakoukoliv jinou - a na konec vám na výstupu vyhodí další komplexní číslo. Ve volné přírodě poznáte komplexního trpaslíka snadno - na rozdíl od svého reálného kolegy má na hrudi vytetované kapitánské céčko (C = complex).
Ta vstupní proměnná se obvykle značí z a ta výstupní w. Komplexní funkce tedy nemají obecný tvar y = f(x) ale w = f(z).
Většina užitečných pojmů (definiční obor, obor hodnot, spojitost, linearita, inverzní funkce, derivace) se dá převzít přímo z reálné analýzy a s jejich definicí nejsou těžkosti.
Úplně všechno se ale do komplexního jazyka přeložit nedá. Třeba monotonie by se definovala jen ztěžka, protože na komplexních číslech - na rozdíl od těch reálných - neexistuje přirozené uspořádání, které by nám vždy umožnilo rozhodnout, které ze dvou čísel je větší (je např. íčko větší než jednička nebo menší?). Proto pojmy jako funkce rostoucí nebo klesající v komplexním oboru moc smyslu nedávají.
Další velký problém nastane v okamžiku, kdy se danou komplexní funkci budeme snažit nakreslit.
V reálné analýze je to jednoduché. Vstup i výstup jsou jednorozměrná "čísla", takže znázornění funkce se provede v dvourozměrné rovině x-y. Z obrázku pak lehce odečteme, jak jsou jednotlivé vstupy (x) přeměňovány na výstupy (y).
U komplexních funkcí je vstup i výstup de fakto dvourozměrný (komplexní číslo je bod v rovině) a tak na ekvivalentní "obrázek" bychom potřebovali čtyřrozměrný graf (dvě dimense na osu w a další dvě na osu z) a něco tak divokého by naše oči nezvládly.
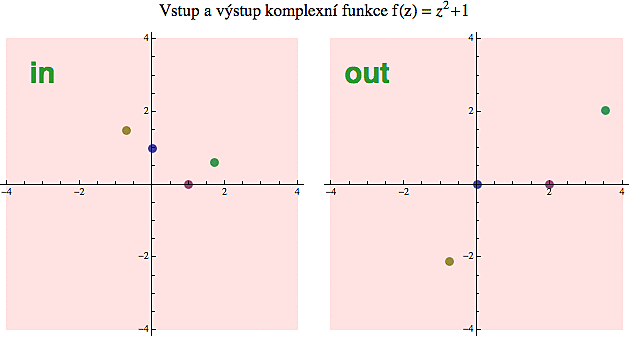
Prozatím si je tedy budeme představovat tak, že si vytvoříme dvě kopie komplexní roviny - jednu pro vstup (in) a druhou pro výstup (out). Ve vstupní rovině si vybereme nějaký bod (komplexní číslo), hodíme ho trpaslíkovi do krabičky a vypadne nám výstupní komplexní hodnota (také bod), kterou vyneseme ve výstupní rovině.
Na dalším obrázku je to schematicky vyznačeno pro funkci f(z) = z2+1. Bod z=i (modrý míček) se zobrazí na výstupní hodnotu w = 0. Sami si můžete ověřit, co se stane s míčkem v bodě z=1 (červený). Další dva míčky sedící v obecných desetinných číslech jsem zobrazil počítačem. Toto je velmi hrubý nástin chování funkce f, ale prozatím nám to bude stačit.
Tento obrázek nám také umožní pochopit princip inverzní funkce. Stejně jako v reálném případě, inverzní funkce převádí výstupy zpět na vstupy. Pokud daná funkce zobrazuje z na w, tak funkce inverzní musí zobrazit w zpátky na z. Původní funkce tedy bere vstupní "míčky" a přiřazuje jim "míčky" výstupní, zatímco funkce inverzní dělá pravý opak - z míčků výstupních dělá míčky vstupní. Naše funkce z2+1 přiřadila bodu z=i (modrý míček) výstupní hodnotu w = 0. To znamená, že inverzní funkce, což je v podstatě sqrt(w-1), musí zobrazit 0 na i.
Spojitost funkce - stejně jako v reálném případě - znamená, že malá změna vstupní proměnné zaručuje malou změnu proměnné výstupní. A tu velikost respektive malost změny dokážeme celkem lehce kvantifikovat pomocí absolutní hodnoty rozdílu. Žádný velký problém nepředstavuje ani derivace a s ní spojený pojem "hladkosti". Hladké komplexní funkce - zvané holomorfní nebo též analytické - patří k nejužitečnějším objektům komplexní analýzy (ty si ale vyžádají zvláštní Matykání).
Dalším důležitým a z reálné analýzy lehce přenositelným pojmem je kořen funkce - tedy taková vstupní hodnota z, která nám na výstupu dá nulu. Snaha o jeho nalezení vede k řešení rovnice: f(z)=0 (tady mám samozřejmě na mysli komplexní nulu: 0+0i). V jednoduchých případech se ty kořeny dají najít algebraicky, tak jako to dělávaly naše babičky, v obtížnějších se hledají pomocí numerických metod.
+++++++++
Nejznámějšími funkcemi jsou polynomy. Tedy funkce odvozené z aritmetických operací, kde se dá ta výstupní hodnota spočítat přímo z vlastností komplexních čísel. Například funkce w=z2 funguje přesně tak, jak si asi představujete. Hodíte do ní i, vypadne vám f(i) = -1. Hodíte do ní 5, vypadne vám f(5) = 25. Vhodíte 2+i, vypadne vám f(2+i) = 3+4i. Pro každé číslo z vám trpaslík na výstupu podá jeho čtverec z2 - nic víc v tom není.
Pro polynomy vyšších stupňů se vyplatí znát mocniny i. Není to nic těžkého, prostě každou předchozí vynásobíme dalším íčkem a zjednodušíme. Takže například i3 = i2 * i = (-1)*i = -i. A obdobně pro ty další. Nakonec dostaneme tuto posloupnost (a začnu nultou mocninou):
1,i,-1,-i,1,i,-1,-i,1,i,-1,-i,1,i,...
(ty čtyři první mocniny se vlastně stále točí dokola)
Můžete si to procvičit na funkci w = g(z) = z3 - 2z + 1.
Její hodnota v bodě i je snadná: g(i) = i3 - 2i + 1 = -i -2i+1 = 1-3i
A kdo si chce započítat, může si zkusit ukázat, že g(2-3i) = -49-3i.
Experti si mohou troufnout i na desetinná čísla: g(1.2+0.7i) = -1.436+1.281i
Ovšem nejen polynomy živ je matematik. Nejdůležitější funkcí - a v komplexním případě to platí dvojnásob - je stále exponenciela. Ta všudypřítomná tetička známá v reálném případě jako "é na x" alias exp(x).
+++++++++
Komplexní exponenciela
Důležitou vlastností reálné exponenciely je, že převádí součet na součin, tedy že pro každou dvojici reálných čísel a,b platí exp(a+b) = exp(a)*exp(b). Tento vztah nám umožní nahlédnout i do struktury komplexní exponenciely (která se nedá přímo dovodit z algebraických vlastností komplexních čísel, protože jsme si zatím neřekli, jak umocnit reálné číslo - zde e - na komplexní exponent).
Nuže vezměme si nějaké komplexní číslo z = x+iy a šup s ním do trpaslíkovy krabičky:
exp(x+iy) = exp(x)*exp(iy)
Ta první část výrazu napravo je jasná - to je obyčejná reálná exponenciela. Stačí tedy, když pochopíme, co exponenciela dělá s čísly imaginárními (násobky íčka) a máme vystaráno.
To ale není nikterak jednoduchý problém a budeme se muset odkázat na vyjádření transcendentních funkcí pomocí nekonečných polynomů. Tyto polynomy (přesněji řady) nám vlastně ukazují, jak se dá daná funkce přeformulovat pomocí (nekonečně mnoha) algebraických operací (a ty už s íčkem umíme docela dobře).
(stále jsem vám ještě neprozradil, jak si ty nekonečné polynomy spočítat - k tomu se dostaneme, až se vrátíme k diferenciálnímu počtu. Zatím si je představujte jako aproximace, s tím, že čím více členů na pravé straně si vezmete, tím lepší aproximaci získáte. A pokud si je vezmete všechny, podaří se vám tu funkci zrekonstruovat přesně)
A teď s těmi nekonečnými polynomy začneme čarovat.
Nejprve si do (1) dosadíme ix abychom viděli, co to mysteriózní íčko s naší exponencielou udělá. Pak si v (5) všechny mocniny íčka zjednodušíme (viz závěr předchozí sekce) a v (6) následně odseparujeme výrazy, které íčko obsahují, od těch, které ho neobsahují. V (7) to íčko vytkneme, zbylé členy zjednodušíme a pak si uvědomíme, že v závorkách máme de facto nekonečné polynomy pro sin a cos - viz (2) a (3) - a tím dostaneme závěrečný vztah, slavnou Eulerovu formulku (8). Rovnice (9) už pak jen všechno smontuje dohromady v komplexní exponencielu (a tam už imaginární část značím y).
Teď už tu nejkrásnější rovnici světa máme takřka na dosah. Stačí si do (8) dosadit x = ? (což je úhel v radiánech odpovídající 180°). Pravou stranu si buď vyčíslíme pomocí sínu a kosínu a nebo si uvědomíme, že na jednotkové kružnici odpovídá 180° (měřeno od kladné osy x) právě bodu -1. Takže dostaneme exp(i?)=-1 a jsme doma.
Mimochodem, i známá Moivreova věta je důsledkem rovnice (8):
(cos(x)+i sin(x))^n = (exp(ix))^n = exp(inx) = cos(nx) + i sin(nx)
(zde je záhodno učinit přestávku na svačinu)
+++++++++
Dalším důsledkem této malé odyssey do světa řad je pozoruhodný fakt, že exp(ia) je komplexní číslo na jednotkové kružnici, odpovídající úhlu a (v radiánech!). Jak se reálné číslo a zvětšuje, bod exp(ia) obíhá po kružnici proti směru hodinových ručiček pořád dokola. Z rovnice (9) dále vypývá, že komplexní exponenciela je periodická funkce s periodou 2?i, tj. kdykoliv si vezmeme dva body lišící se o tuto hodnotu, exponenciela je zobrazí na stejný bod ve výstupní rovině.
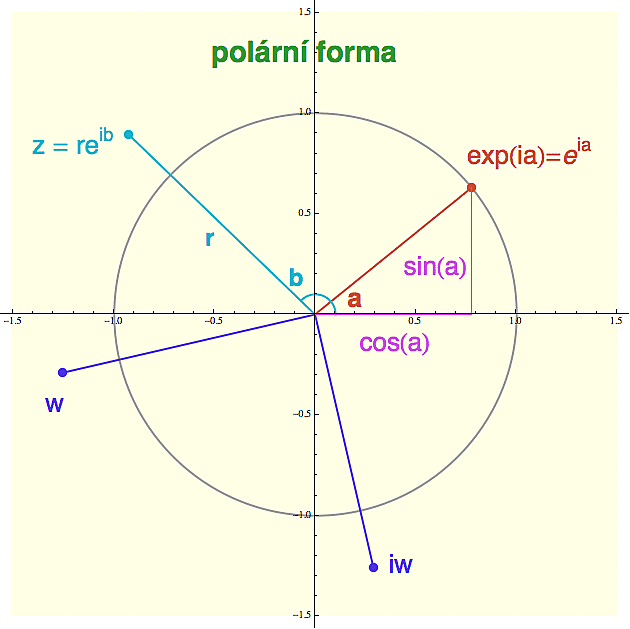
Komplexní exponenciela nám také umožňuje vyjádřit polární souřadnice komplexního čísla ve velmi kompaktní formě (viz níže bleděmodrý bod s poloměrem r a úhlem b - měřeným od kladné osy x).
z = r*exp(ib)
Samozřejmě bychom ty souřadnice mohli vyjádřit klasicky:
x = r cos(b)
y = r sin(b)
ale při algebraické manipulaci bychom pak museli ty síny a kosíny neustále přehazovat vidlema a taková věc se brzy omrzí.
Polární forma komplexního čísla nám poskytuje nový pohled na mechaniku komplexního násobení. Zatímco v kartézských souřadnicích vypadá celkem neprůstřelně, v polárních má velmi jednoduchou formu:
r*exp(ia) * s*exp(ib) = rs * exp(i(a+b))
Při součinu dvou komplexních čísel zapsaných v polárních souřadnicích prostě vynásobíte poloměry a sečtete úhly.
Jako jednoduchý příklad si ukážeme, co se stane, když dané komplexní číslo w=r*exp(ic) vynásobíme íčkem (viz modrá část obrázku nahoře). Íčko se polárně vyjádří jako exp(i?/2), kde ?/2 je pravý úhel vyjádřený v radiánech (poloměr tady nepotřebujeme, protože abolutní velikost íčka je 1). Vynásobení čísla w íčkem tedy v polárních souřadnicích vypadá takto:
r*exp(ic) * exp(i?/2) = r * exp(i(c+?/2))
a to znamená, že po vynásobení se číslo w prostě pootočí o pravý úhel (jeho polární úhel c se zvětší o ?/2). Kdo ovládá vektory, může si tu kolmost odvodit i z kartézského vyjádření. Pokud je w=x+iy, bude iw = -y+ix a vektor {-y,x} je samozřejmě kolmý na ten původní {x,y} (jejich skalární součin je nula).
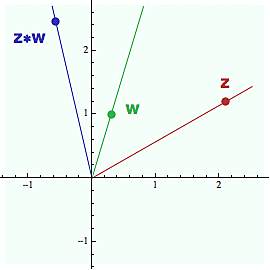
Ten součin v polárních souřadnicích také znamená, že si jeho fungování můžete představit pomocí následující vizuální hračky (viz obrázek vpravo).
Vezmeme si dvě komplexní čísla, z a w a zakreslíme si jejich součin z*w (modrý míček). Když teď budeme s těmi čísly z a w pohybovat po naznačených polopřímkách, tedy tak aby jejich polární úhel byl stále stejný, pak jejich komplexní součin (modrý míček) bude také muset zůstat na modré polopřímce (nezměnili jsme polární úhel z ani w, takže se nesmí změnit ani polární úhel z*w - který je jejich součtem). A můžete si rozmyslet, jaký vliv má na pohyb modrého míčku současné posunování tím zeleným a červeným.
Z tohoto pohledu vyplývá, že komplexní násobení není zase tak úplně neintuitivní, jak by se mohlo zdát z jeho kartézského vyjadření, a určité přirozené zákonitosti splňuje.
+++++++++
Podívejme se teď na rovnici komplexní exponenciely w=exp(z) ještě jednou:
w = exp(x+iy) = exp(x) * exp(iy) = r * exp(iy)
Výraz exp(x) je vždy kladné číslo a můžeme si ho tedy představit jako polární poloměr r. Exponenciela tedy v jistém smyslu převádí kartézské souřadnice na polární.
A tady si dovolím malou filosofickou odbočku.
Komplexní číslo - jakožto bod v rovině - má v podstatě dvě formy vyjádření. Algebraická z = x+iy odpovídá kartézským souřadnicím, zatímco exponenciální z = r*exp(ia) odpovídá souřadnicím polárním (poloměr r a úhel a). Tyto formy mají velmi rozdílné vlastnosti co se týče základních aritmetických operací -- sčítání a odčítání.
Kartézské souřadnice jsou velmi snadné - a přímo bych řekl intuitivní - pokud se jedná o součet. Prostě sečtete příslušné souřadnice - reálné a imaginární části - separátně.
(a+ib) + (c + id) = (a+c) + i (b+d)
Násobení - jak jsem poznamenal výše - už je trochu neintuitivní
(a+ib) * (c + id) = (ac-bd) + i (ad+bc)
U polárních souřadnic je tomu naopak. Násobit v nich je přímo pohoda:
r*exp(ia) * s*exp(ib) = rs * exp(i(a+b))
Se součtem je to horší. Možná si říkáte, že součet dvou čísel vyjádřených v polárních souřadnicích by se také měl dát zmáknout (tedy vyjádřit nějakou změtí daných polárních poloměrů r,s a úhlů a,b). No tak si to schválně zkuste:
r*exp(ia) + s*exp(ib) = grrrrrrr... vrrrrrrr... arrrrgh...
Ne, není to žádná legrace. Samozřejmě spočítat se to dá - a nebudete na to potřebovat víc než středoškolskou matematiku - ale není to podívaná pro slabé žaludky (kdo si na to troufá, může se mrknout sem).
A co tím chtěl básník říci?
Básník tím chtěl říci, že v matematice - zejména v teorii čísel - je spousta problémů, které souvisí s tím, že sčítání a násobení jsou v jistém smyslu nekompatibilní operace. Například spočítat faktorizaci součtu dvou čísel, jejichž rozklad na prvočinitele známe, je zatraceně těžký úkol. A podle mého soudu jde část této obtížnosti na vrub skutečnosti, že komplexní sčítání "žije" v kartézských souřadnicích, zatímco komplexní násobení "žije" v souřadnicích polárních (jak jsme právě viděli). A tyto dvě souřadnicové soustavy jako by byly z jiného světa. Jedna z Marsu a druhá z Venuše.
A pokud mi dovolíte domlátit tuhle lacinou analogii až na samou dřeň její existence - jak by řekl jiný básník - uzavřu tuto podsekci nekorektní genderovou hypotézou, že muži přemýšlejí v soustavě kartézské, zatímco ženy v soustavě polární. Haha, zasmáli se zbrojnoši...
+++++++++
(a ještě něco pro příznivce sínu a kosínu)
Z Eulerovy rovnice (8) se dá odvodit i zajímavý vztah mezi exponencielou a goniometrickými funkcemi (který v reálné analýze vůbec není vidět). Napíšeme si ji jak pro kladný, tak záporný úhel x:
exp(ix) = cos(x) + i sin(x)
exp(-ix) = cos(-x) + i sin(-x) = cos(x) - i sin(x)
sečtením a odečtením těchto rovnic dostaneme tyto vztahy:
cos(x) = (exp(ix)+exp(-ix)) / 2
sin(x) = (exp(ix)-exp(-ix)) / (2i)
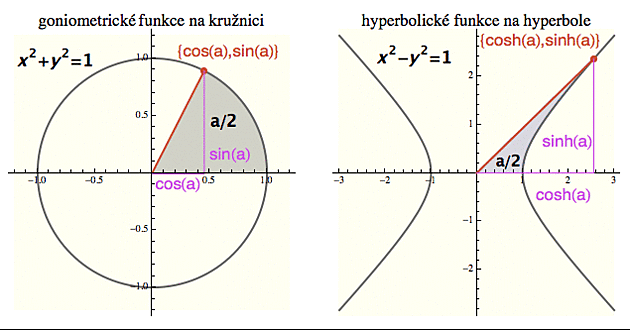
Ty můžeme považovat za definici komplexních goniometrických funkcí (protože žádné trojúhelníky s komplexními úhly v praktickém životě stejně nenajdeme). Pokud si ze školy pamatujete definici funkcí sinh (hyperbolický sínus) a cosh (hyperbolický kosínus), najdete v jejich vzorečcích jistou podobnost:
cosh(x) = (exp(x)+exp(-x)) / 2
sinh(x) = (exp(x)-exp(-x)) / 2
To vlastně znamená, že z pohledu komplexních čísel jsou goniometrické a hyperbolické funkce prakticky jedno a to samé. Stačí vyměnit x za ix.
cosh(x) = cos(ix)
sinh(x) = i sin(ix)
Uvážíme-li, že násobení íčkem odpovídá pootočení o 90 stupňů, můžeme se na hyperbolický kosínus z pohledu komplexní analýzy dívat jako na "běžný" kosínus pootočený o 90 stupňů. Hodnota hyperbolického kosínu řekněme v bodě z=2+i je tedy to samé co hodnota kosínu v bodě pootočeném o 90 stupňů, což je iz = i(2+i) = -1+2i. Takže suma sumárum:
cosh(2+i) = cos(-1+2i).
Jak jsem poznamenal výše, grafy komplexních funkcí jsou trochu komplikované, ale kdybyste někdy potkali čtyřrozměrného mimozemšťana, který by měl k disposici graf komplexního kosínu vymodelovaný třeba na dřevěné desce, tak graf hyperbolického (komplexního) kosínu byste si mohli prohlédnout tak, že byste tu jeho dřevěnou desku prostě pootočili o 90°.
Tohle ukazuje na velkou sjednotitelskou roli komplexní analýzy. Goniometrické i hyperbolické funkce jsou si zde navzájem sourozenci (obě skupiny jsou jen kombinacemi komplexních exponenciel). Z pohledu reálné analýzy taková souvislost obou kosínů (a sínů) není vidět.
Možná si ze střední školy vzpomenete, že funkce sin a cos popisují pohyb bodu po kružnici, zatímco jejich hyperboličtí bratři, sinh a cosh, popisují pohyb bodu po hyperbole (na obrázku níže vidíte příslušné kartézské souřadnice těch bodů). Pokud si ty funkce vykreslíte na grafické kalkulačce, budou se vám reálně jevit jako dvě dvojice zcela nesouvisejících funkcí, přestože jedny jsou jen pootočením těch druhých v komplexní rovině (jak jsme právě viděli).
Ten parametr a má v obou případech stejný význam - je to dvojnásobek vystínované plochy. To v případě kružnice (vzpomenete-li si na vzoreček pro obsah kruhové výseče) přesně odpovídá úhlu v počátku - jak jsme viděli výše. U hyperboly by vám to s tím úhlem ale neprošlo (více podrobností najdete zde).
Mimochodem to, že ryze imaginární exponenciela popisuje pohyb po kružnici, se dá vysvětlit i jinak - trochu fyzikálněji. Představte si, že t je čas a my sledujeme pohyb bodu, jehož poloha v rovině je dána výrazem exp(it). To znamená, že v čase nula má náš bod polohu {1,0}, což je souřadnicové vyjádření pro exp(0)=1+0i. Pro derivaci reálné exponenciely platí, že (exp(at))' = a exp(at), takže pokud ta komplexní exponenciela má být co k čemu, měla by splňovat totéž: (exp(it))' = i exp(it). To ale znamená, že náš bod se pohybuje tak, že vektor jeho rychlosti (levá strana) je vždy kolmý na vektor polohy (pravá strana), protože - jak jsme viděli výše - násobení íčkem vytváří kolmý vektor. Takže hledáme křivku, jejíž tečný vektor (rychlost) je kolmý na vektor polohy. A to se dá udělat dvěma způsoby - buď si sestavíme diferenciální rovnici, ze které skutečně dostaneme, že hledanou křivkou je jednotková kružnice a nebo si vzpomeneme ze střední školy na poučku, že právě kružnice má tu vlastnost, že její tečný vektor je kolmý na vektor polohy (což je zde radius-vektor).
+++++++++
Sekce Jauvajs: Komplexní logaritmus
jen pro mimořádně otrlé povahy
Logaritmus je inverzní funkcí k exponenciele. Jeho reálná verze je celkem jednoduchá - je to funkce všude rostoucí, všude konkávní, žádné lokální extrémy nemá, zkrátka studenta u zkoušky s ní moc nepotrápíte. Komplexní logaritmus je naproti tomu pěkně protřelý prevít. Abychom jeho vrtochy pochopili, musíme si nejprve na komplexní exponencielu pořádně posvítit.
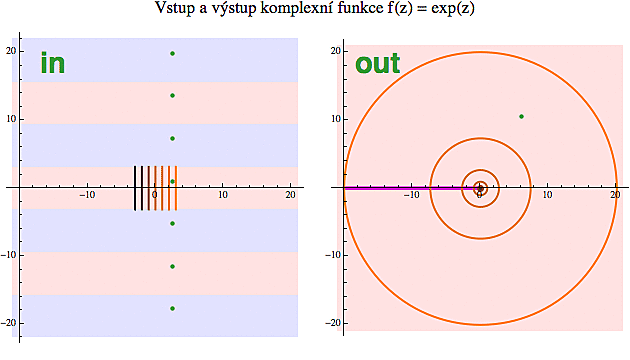
Následující dvojobrázek ukazuje jak exponenciela zobrazuje vstupní hodnoty (in) na výstupní (out). Připomeňme si její formulku:
exp(x+iy) = exp(x) * exp(iy)
Jak jsme zjistili v předešlé sekci, ten výraz napravo je de facto polární formou komplexního čísla. Výraz exp(x) nám udává poloměr (pro každé x je to kladné číslo) a exp(iy) je bod na kružnici, odpovídající polárnímu úhlu y.
Nejprve se podívejme na ten uzoučký růžový proužek kolem osy x (jeho šířka odpovídá rozmezí od -? do ? na ose y). Každá z těch naznačených vstupních úseček (které mají konstantní x) se na výstupu exponenciely zobrazuje na kružnici o poloměru exp(x). Pro záporná x bude hodnota exp(x)<1, takže ty kružnice je stěží vidět, ale jak se x zvětšuje, poloměr příslušných kružnic roste také. Když v duchu pro každou úsečku projedete s hodnotou y od -? do ? (tedy od spodního okraje proužku k tomu vrchnímu), na kružnici tomu bude odpovídat úhlový pohyb od -? do ? (tedy od -180° do 180°).
Odvážnější jedinci si mohou představit, jak by exponenciela zobrazovala přímky horizontální (tedy kolmé na ty vyznačené úsečky). Pro ně bude y konstantní, takže ten druhý člen v definiční rovnici nahoře bude odpovídat konstantnímu úhlu a když v duchu projedete s x od mínus nekonečna do plus nekonečna, tak ten první člen proběhne od 0 do nekonečna. To znamená, že obrazem takové přímky bude v rovině výstupní (out) paprsek směřující z počátku pod úhlem y (kde y je dané tou vstupní přímkou).
(na tomto obrázku vidíte, jak exponenciela převádí kartézské souřadnice na polární)
Důležité je uvědomit si, že zatím mluvíme pouze o tom prostředním růžovém proužku. Z diskuse výše vyplývá, že exponenciela zobrazuje tento proužek (vlevo) na celou komplexní rovinu (vpravo) s výjimkou bodu 0 (!). Komplexní exponenciela - stejně jako ta reálná - nemá žádný kořen, to znamená, že žádné číslo (ani reálné, ani komplexní) nedokáže zobrazit do nuly.
Ty ostatní proužky vlevo už tedy nic nového nepřinášejí, pouze opakují hodnoty, které už jsme jednou viděli. To si můžete ověřit tak, že podél jedné té úsečky nalevo budete v duchu pokračovat dál do vyšších a vyšších proužků. Odpovídající obraz (napravo) takového pohybu bude bod neustále obíhající podél příslušné kružnice (jejíž poloměr je určen hodnotou x dané úsečky). To je opět důsledkem toho, že exponenciela má periodu 2?i (2? je šířka každého proužku).
To opakování hodnot je na obrázku ilustrováno zelenými body (vlevo), které se všechny - bez rozdílu - zobrazují do jediného zeleného bodu vlevo. To samozřejmě při definici inverzní funkce způsobuje velký problém, protože není jasné, který z těch bodů vlevo bychom měli inverzní funkci (a to je komplexní logaritmus) vlastně přiřadit.
Tato nejednoznačnost se ošetří úplně stejně jako při konstrukci inverzní funkce k sínu (a to je arcsin). Tam jsme prostě definiční obor zúžili tak, aby se nestalo, že by dvěma různým hodnotám x odpovídalo stejné y. Tady uděláme to samé. Prostě si ze všech těch proužků vybereme jen jeden a na ten naši exponencielu omezíme. V každém takovém proužku je zelený bodík pouze jeden, takže inverzní trpaslík nebude mít s přiřazením potíže.
V praxi si samozřejmě vybereme skoro vždycky ten prostřední růžový proužek, ale ve speciálních případech si můžeme vybrat i jiný, exponencielu omezit na něj a dostaneme pak trochu jiný logaritmus - technicky říkáme, že dostaneme jinou "větev logaritmu".
Pokud se tedy omezíme jen na ten prostřední růžový proužek, dostaneme tzv. hlavní větev logaritmu a pro ni si odvodíme celkem jednoduchou rovnici. Vyjádříme si číslo w (v pravé části obrázku) v polárních souřadnicích w = r*exp(ia) a budeme hledat, jaké číslo z=x+iy (vlevo) se nám do tohoto bodu zobrazí. To bude logaritmus čísla w. Podle diskuse na začátku sekce, je exp(x) = r, takže dostaneme x = ln(r), no a polární úhel a bude přímo odpovídat hledanému y (viz definiční rovnice exponenciely). Pro komplexní logaritmus tak dostaneme poměrně snesitelný vzoreček:
log(w) = ln(r) + ia = ln(Abs(w)) + i Arg(w)
kde jsem použil značení pomocí absolutní hodnoty (což je de facto polární poloměr) a argumentu (polární úhel) čísla w. A protože je jedno jaká písmenka pro značení používáme, přejdeme v definici inverzní funkce k běžnějšímu z:
log(z) = ln(Abs(z)) + i Arg(z)
(ln zde značí obvyklý přirozený logaritmus reálných čísel)
+++++++++
Na ten problém s jednoznačností se teď můžeme podívat i z druhé strany - tedy ze strany logaritmu. Představte si, že v pravé části obrázku pochodujete podél jedné z těch polárních kružnic a průběžně počítáte logaritmus čísla, ve kterém se nalézáte.
Reálná část logaritmu nepředstavuje problém, protože na té kružnici je absolutní hodnota konstantní, takže si v té formulce výše moc nezapočítáte. Musíte ale dávat bacha na polární úhel, který určuje imaginární složku (a počítejme to pro jednoduchost ve stupních i když v tom logaritmu to samozřejmě musíte udat v radiánech). Takže vystartujeme ze záporné osy x (na obrázku fialově) s úhlem -180°. Jak postupujeme proti směru hodinových ručiček, úhel nejprve utěšeně klesá -170°, -160°, -150°..., ale pak přelezeme kladnou osu x a za ní nám opět začne narůstat 0°, 10°, 20°...
Jenže až tu celou kružnici obejdeme (a začneme se opět blížit k záporné ose x), úhel začne nabývat hodnot 160°, 170°, 180° - a tady stop! Dál nemůžeme. Kdybychom postupovali dál podél kružnice, dostali bychom se tam, kde už jsme jednou byli a úhel by nám najednou začal nesouhlasit s tím předchozím nálezem - my ten úhel v komplexním logaritmu nemůžeme jednou definovat jako -170° a podruhé jako 190°. Funkce musí jednomu vstupu - jednomu bodu na kružnici - přiřadit pouze jeden výstup. A tady bychom pro jedno komplexní číslo z (na kružnici kousek pod tou fialovou polopřímkou) dostali dva různé úhly - a tedy dvě různé hodnoty logaritmu. V reálném případě je tato funkce definována prostě jen na jedné polopřímce z nuly (kladná osa x), takže tam žádné problémy s polárním úhlem nevznikají.
Tato patálie se dá vyřešit dvojím způsobem.
První možnost je, že do komplexní roviny postavíme pevnou zarážku, která nám znemožní ty polární kružnice procházet vícekrát. To se udělá tak, že se z počátku vyšle nějaká polopřímka (na obrázku výše vpravo je znázorněna fialově podél záporné osy x) a na této polopřímce prohlásíme komplexní logaritmus za nedefinovaný. Tu polopřímku z počátku si můžeme vybrat celkem libovolně, ale záporná osa x je nejčastější volbou (polární úhel pak probíhá od -180° do 180° a díky té vyhozené polopřímce se vyhneme výše popsané nespojitosti). Samozřejmě bychom také mohli vyhodit kladnou osu x, ale to bychom si zbytečně znemožnili výpočet komplexního logaritmu pro kladná reálná čísla.
Druhá, a poměrně exotická, možnost spočívá v tom, že si komplexní rovinu představíme jako koberec, který rozstřihneme podél té fialové polopřímky. No a v okamžiku, kdy se při našem pohybu podél kružnice dostaneme zpět ke 180° (a chtěli bychom pokračovat do těch zakázaných 190°), tak na komplexní rovinu hodíme další rozstřihnutý koberec a oba sešijeme podél těch fialových rozparků takto. Vrchní okraj (tedy ten, který odpovídá kladným hodnotám y) rozparku na spodním koberci sešijeme se spodním okrajem (který odpovídá záporným hodnotám y) rozparku horního koberce a pak vesele pokračujeme dále, protože na tom koberci "nahoře" jsme ještě logaritmus nedefinovali, takže tam si těch 190° můžeme klidně lajsnout aniž bychom se dostali do sporu s předchozí definicí. No a až se otočíme o dalších 360° hodíme na komplexní rovinu třetí koberec, který opět sešijeme stejným způsobem a takhle pokračujeme pořád dál, močálem temným kolem bílých skal.
Touto bizarní konstrukcí dostaneme funkci logaritmus, která bude jednoznačně definovaná ne v komplexní rovině, ale na podivné nestvůře sešité z nekonečně mnoha koberců (její struktura trochu připomíná spirálovité schodiště). Této nestvůře se říká Riemannova plocha komplexní funkce logaritmus.
Z praktického pohledu je lepší se spokojit s tou nespojitostí a definovat logaritmus jen mimo fialovou úsečku. Pro většinu aplikací to stačí. Mimochodem, ten (úhlový) skok, který bychom přechodem úsečky prodělali se přenáší i na funkce z logaritmu odvozené, jako je např. druhá odmocnina, kterou můžeme vyjádřit takto:
sqrt(z) = exp(log(z)/2)
I v její definici si musíme vybrat, zda se spokojíme s nespojitostí podél nějaké vyhozené polopřímky a nebo se pokusíme sestrojit její Riemannovu plochu. To už jsou ale poměrně náročné úlohy i pro experty, takže si s tím nebudeme lámat hlavu.
+++++++++
A protože komplexní logaritmus je opravdu tvrdý oříšek, dáme si dnes na uklidněnou něco louskavého. Marie Rottrová: Skořápky ořechů.
Předchozí díly Matykání.
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
Jan Řeháček
Co rok dal

Začátek nového roku je tradičně příležitostí k ohlédnutí za rokem starým, takže jsem prohrábl archív a vylovil z něho pár fotografií z našeho parku, které si nenalezly cestu do některého z předchozích tématických blogů.
Jan Řeháček
Politické školení mužstva: Pyšná princezna

Roto končit! Pozor! (vejde útvarový politruk) Soudruzi vojáci, kapitál se potácí. Ale sám se nám na smetiště dějin nevypotácí. My mu musíme co, soudruzi? No? Nikdo? No, my mu musíme pomoci, vy hlavy hovězí!
Jan Řeháček
Ten podzim se nám hezky vybarvil

Každý podzim je v našem parku trochu jiný. Stromy, které by loni přešminkovaly i šestnáctku před prvním rande, jsou letos pobledlé jako Rusalka. A ty, které se zprvu barevně upejpaly, se najednou utrhly z řetězu. Jak řezníkův pes.
Jan Řeháček
Paroháčů je letos dost

Srnka je v našem parku jako houska na krámě. Zato setkání s jelenem si člověk musí považovat. Letos jsem ale náhodou objevil, kde se srocují: na záložním travnatém parkovišti, kterému se říká Gil's Hill, těsně před západem slunce.
Jan Řeháček
Chřadnoucí prales - pod vodou i nad ní

O korálovém útesu se říká, že je to "dešťový prales" oceánu. Biodiversita, kterou reprezentuje je ohromující. Totéž platí i o jeho suchozemském ekvivalentu. Bohužel, oba ekologické systémy se dostávají na seznam ohrožených druhů.
Jan Řeháček
Letní kvítí

Primární sezónou květů je sice jaro, ale ani léto není v našem parku z pohledu barev úplná nuda. Tady je malá fotovonička složená z příspěvků místní flory. Aneb kdo nekvete s námi, kvete proti nám.
Jan Řeháček
Plody léta

Léto je časem zrání a ani v našem parku tomu není jinak. Zajímavé plody nabízí říše rostlinná i živočišná. Tady je malý průřez letošní nabídkou: asijské maliny, kuriózní houby a malí mývalové. Ceny jsou mírné: léto létá zdarma.
Jan Řeháček
Kvetoucí fuga (Beethoven)

V Beethovenově Misse Solemnis nalezneme spoustu skrytých drahokamů, které zde leží prakticky nepovšimnuty, protože celková hudební struktura této Mše je na první poslech naprosto neprůstřelná. Jedním z nich je fuga v závěru Creda.
Jan Řeháček
Sovy a supi

V našem parku také poletuje spousta zajímavých ptáků. Tak jsem jich pár vyfotil. Sovy jsou sice nočními živočichy, ale na jaře se občas dají zastihnout i za denního světla. A za pár šupů k nim přihodím ještě pár supů. Ať nežeru.
Jan Řeháček
Vlčí západy

Při procházkách naším parkem občas fotím západy slunce z vyvýšeného travnatého parkoviště zvaného Gil's Hill. Říkám jim Vlčí západy. Jednak proto, že mají zhusta barvu vlčích máků a jednak proto, že náš park se jmenuje Vlčí past.
Jan Řeháček
Za devatero fotkami: Malebné peklo

Já to tušil, že jednou skončím v pekle. Jen jsem si představoval, že vstup bude mít z nějaké islandské sopky. Houbeles! Jeho vchod se nalézá poblíž vesničky Medkovy Kopce nedaleko Hlinska. "Lasciate ogne speranza, voi ch'intrate".
Jan Řeháček
Sedm divů jara

Po dlouhém barevném půstu zimní šedi působí návrat jarní kavalerie jako zjevení. V našem parku v tomto období kvete několik dřevin, s jejichž uměleckými kreacemi bych vás v tomto blogu rád seznámil. Matička příroda dokáže kouzlit.
Jan Řeháček
strž

V dnešním pokračování poetického cyklu "Bez básně a Hany" se nedozvíme jakou krevní skupinu mají nejraději novozélandští upíři a zda je tuna pampeliškového chmýří těžší než sbírka maturitních příkladů z matematiky.
Jan Řeháček
Devět zastavení času

Příroda se mění pomalu, ale jistě. Den ze dne nic nepostřehnete, ale když se na známá místa vrátíte za pár týdnů, naleznete desítky drobných změn. Tak jsem se na třech místech našeho parku devětkrát zastavil, abych je zachytil.
Jan Řeháček
Cesta do hlubin duše (Beethoven)

Lidská duše je odvěkou hádankou, na které si vylámaly zuby celé generace psychologů, teologů a filosofů. Tajuplný komplex uvnitř každého z nás. Pro mne je definicí lidské duše Beethovenův 14. smyčcový kvartet cis moll, op. 131.
| předchozí | 1 2 3 4 5 6 7 ... | další |
- Počet článků 402
- Celková karma 19,53
- Průměrná čtenost 920x