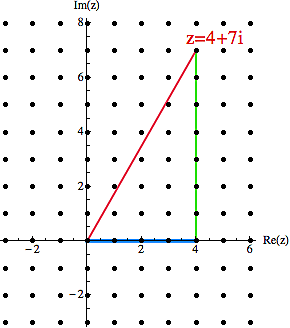Matykání: jak si nabrnkat pythagorejské trojice
Když se na základní škole učíme počítat s reálnými čísly, paní učitelka na nás nevybalí hned éčko a píčko, ale nejprve nás naučí počítat s celými čísly, potom se zlomky a teprve nakonec s čísly iracionálními. Koneckonců, už Jan Ámos nás nabádal, abychom postupovali od jednoduššího ke složitějšímu a ne naopak.
V komplexním oboru to platí dvojnásob. A tak dnes začneme plavbu íčkovým mořem s objekty relativně jednoduchými - s komplexní verzí celých čísel, kterým se někdy říká Gaussovská celá čísla (ve zkratce Gaussovská čísla), podle německého matematika C. F. Gausse, který měl na vybudování analýzy komplexních čísel lví podíl.
Nejprve se v rychlosti mrkneme na faktorizaci Gaussovských čísel a na komplexní verzi prvočísel a pak už se dostaneme ke slíbenému návodu, jak vyčíslit všechny pythagorejské trojice. Koho zajímá pouze to, může rovnou skočit na poslední dvě sekce, protože to povídání o prvočíslech bude víceméně nezávislé a budeme z něj nakonec potřebovat jen jednu malou rovnici.
Klíčem k pochopení Gaussovských čísel jsou dvě nenápadná tvrzení, objevená dlouho před tím, než byla komplexní čísla plně prostudována a akceptována matematickou obcí. Jména obou objevitelů začínají shodou okolností na F.
Fermatova věta o součtu čtverců
Tím prvním objevitelem je Pierre de Fermat, francouzký právník ze 17. století, který se ve volném čase zabýval matematikou a specielně teorií čísel. Jednou z jeho libůstek bylo zkoumat, kdy se dají prvočísla napsat jako součet dvou čtverců, tedy kdy se pro dané prvočíslo p dají najít celá čísla x,y splňující p=x2+y2 (prvočísla - jak je dobře známo - se nedají faktorizovat, takže takovýmto rozkladem můžeme alespoň trochu nahlédnout do jejich struktury). A zatímco pod Fermatovými okny lomozily kočáry a trubadúři barokní Evropy, slavný amatér učinil tento překvapivý objev:
Prvočíslo p se dá zapsat jako součet dvou čtverců právě tehdy, když je jeho zbytek po vydělení 4 roven 1. A takový rozklad je (až na pořadí sčítanců) jednoznačný.
(když si to rozmyslíte, ta jednoznačnost je vlastně takový malý zázrak: pro velká prvočísla splňující Fermatovu podmínku by člověk očekával, že takových kombinací čtverců bude celá řada, ale není to tak - ať je to prvočíslo jakkoli veliké, najde se taková dvojice vždy pouze jedna - i to nám ukazuje, jak je náš číselný systém precizně vysoustruhovaný)
Obecně se prvočísla dělí na tři kategorie. Dvojka (jediné sudé prvočíslo) je kategorií sama o sobě. Ta zbývající, lichá, se pak dělí do dvou skupin, podle toho, zda po vydělení čtyřkou nechávají zbytek 1 a nebo 3. Symbolicky tyto dvě skupiny zapisujeme vzorcem 4k+1, respektive 4k+3. Podle Fermatova objevu se tedy prvočíslo dá napsat jako součet dvou čtverců pouze je-li tvaru 4k+1.
V komplexní analýze má jeho výsledek zcela fundamentální význam. My z toho rozkladu na součet čtverců dokážeme udělat komplexní faktorizaci - tedy rozklad na součin (v tomto případě dvou) faktorů. Připomeňme si, že pro každé komplexní číslo z=x+iy dostaneme jeho vynásobením s číslem komplexně sdruženým (z*=x-iy) právě součet dvou čtverců:
z . z* = (x + iy) . (x - iy) = x2+y2
Z pohledu celých čísel nám tedy výše uvedená rovnice naznačuje, že reálná prvočísla tvaru 4k+1 se v komplexních číslech dají dále rozložit a zařadí se tedy mezi čísla složená.
Abych pořád nemusel žonglovat s těmi symbolickými vzorečky, budu prvočíslům tvaru 4k+1 (tedy těm, které se v komplexní analýze dají dále rozložit) říkat měkká prvočísla a těm, která se ani v komplexních číslech rozložit nedají (tvar 4k+3) budu říkat tvrdá prvočísla (ale bacha, toto není oficiální terminologie, to bude jen taková dohoda mezi námi).
Pokud nejste zrovna zbláznění do teorie čísel, v praxi si ten rozklad měkkého prvočísla p na součet dvou čtverců najdete nejlépe metodou pokusů a omylů. Především je jasné, že jeden ze sčítanců musí být menší než sqrt(p/2). Kdyby byly oba větší (jak x, tak y), pak by součet jejich čtverců byl větší než p. Tím pádem nám stačí uvažovat pouze čísla mezi 1 a sqrt(p/2) a těch většinou moc není.
Jako příklad si najdeme rozklad čísla 61 (které má tvar 4k+1 neb se dá zapsat jako 61=4*15+1). Sqrt(61/2) = 5.52, takže jeden ze sčítanců musí být číslo mezi 1 a 5 (ten druhý pak dopočítáme z rovnice 61 = x2+y2). Když si s tím budete chvilku hrát, zjistíte, že x=5 je jediná hodnota, pro kterou bude to dopočítané y celé číslo. Dostanete 61 = 52+y2, což znamená y=sqrt(61-25)=6. Takže řešení je 61 = 52+62 a kýžený rozklad prvočísla 61 na komplexní prvočinitele je podle výše uvedené rovnice 61 = (5+6i)*(5-6i). To si můžete ověřit roznásobením.
(koho tahle praktická metoda neuspokojuje, může se podívat sem, jak se ten Fermatův objev vlastně dokazuje - ale je to poměrně drsné technické čtení)
Tady jsou pro názornost všechna měkká i tvrdá prvočísla menší než N=100:
měkká (4k+1): 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97
tvrdá (4k+3): 3, 7, 11, 19, 23, 31, 43, 47, 59, 67, 71, 79, 83
Pokud si je spočítáte, zjistíte, že měkkých je v tomto rozmezí 11, zatímco tvrdých 13. Tato disproporce se ještě zvýší, pokud si sestrojíme podobný výčet pro prvočísla menší než N=1000. V tomto rozšířeném rozmezí najdeme 80 měkkých a 87 tvrdých. A pro čísla menší než milion se propast dále zvyšuje: měkkých prvočísel je zde 39175 a tvrdých už 39322.
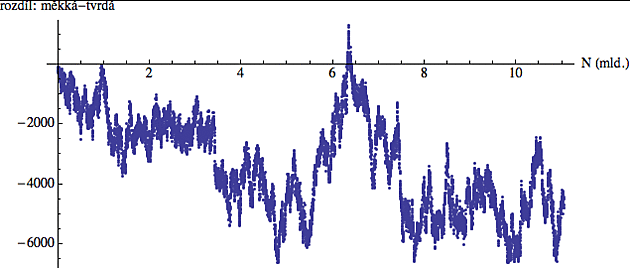
To přimělo ruského matematika Čebyševa v polovině 19. století k vyslovení hypotézy, že v rozmezí 1...N je tvrdých prvočísel vždy o něco více než těch měkkých. Této domněnce se dnes říká Čebyševova tendence (Chebyshev's bias). Pokud by platila a my bychom si pro dané N vykreslili počet tvrdých a měkkých prvočísel v rozmezí 1..N, ta tvrdá by na grafu byla vždy o něco výš než ta měkká (a nebo ekvivalentně: rozdíl "měkká - tvrdá " by byl stále záporný).
Velkou ránu této domněnce zasadil anglický matematik Littlewood, který v roce 1914 dokázal, že v pomyslném "prvočíselném závodě" (zde podrobněji ve formátu PDF) se měkká a tvrdá prvočísla ve skutečnosti střídají ve vedení a těchto prostřídání je nekonečně mnoho. Nicméně nakonec se ukázalo, že ta Čebyševova tendence přece jen v jistém smyslu platí, protože ta měkká prvočísla se ujímají vedení vždy jen "na chvilku" a brzy se opět začne objevovat více tvrdých prvočísel.
Na obrázku níže je ta rozdílová křivka. Pro každé N jsem prostě spočítal tvrdá a měkká prvočísla v rozmezí (1...N) a vynesl rozdíl. A protože jsem to spočítal až do N=11 miliard, vynesl jsem jen každou miliontou hodnotu, aby ten graf nebyl přelidněný. Vidíte, že kolem hodnoty 4.7 miliard už mají tvrdá prvočísla náskok zhruba 6000 a přesto se ta měkká vzchopí a těsně za značkou 6.0 miliard dokonce strhnou vedení na svou stranu. Ale jen na okamžik.
Ta Čebyševova tendence je celkem překvapivá, protože o prvočíslech se všeobecně soudí, že jsou na číselné ose rozložena víceméně náhodně, takže není důvod, proč by po vydělení 4 měla preferovat zbytek 3 a ne 1, tj. proč by ta tvrdá měla být častěji ve vedení než ta měkká a tím pádem ta křivka spíš záporná než kladná. Nicméně numerické experimenty naznačují, že to tak opravdu je (koho zajímají technické detaily tohoto fenoménu, podívejte se sem - je zajímavé, že autoři článku si na pomoc přizvali zatím nedokázanou Riemannovu Hypotézu, o které jsem se zmínil v předminulém Matykání).
Ale abychom se nezamotali do teorie, podívejme se na závěr této sekce, jak ten rozklad na čtverce vypadá pro prvních 30 měkkých prvočísel.
Jakmile si umíte najít takovýto součet čtverců, rozklad měkkého prvočísla na komplexní činitele už je jednoduchý, např.
73 = (3+8i)*(3-8i)
+++++++++
Fibonacciho identita
Druhé tvrzení zmíněné v úvodu nás zavede ještě hlouběji do historie.
Na počátku 13. století objevil italský matematik Fibonacci jednu docela pozoruhodnou rovnici (a přestože se později ukázalo, že o ní věděl už řecký Diophantus a nebo indický Brahmagupta, ve většině učebnic nese jeho jméno):
(a2+b2)*(c2+d2) = (ac-bd)2 + (ad+bc)2
Důkaz této rovnosti si můžete udělat sami tím, že obě strany suše roznásobíte.
Z pohledu předchozí sekce nám tato identita říká, že pokud máme dvě čísla, která se dají zapsat jako součet čtverců, pak i jejich součin se tak dá napsat. A to není úplně triviální, protože zdaleka ne každé číslo je součtem čtverců, ať prvočíslo nebo složené. Z minulé sekce víme, že tvrdá prvočísla se takto zapsat nedají a obecněji platí, že čísla, jejichž prvočíselný rozklad obsahuje tvrdá prvočísla na liché mocniny, se také nedají zapsat jako součet čtverců (např. 35, 44, 54 atd).
Skutečný význam této identity ale spočívá v komplexní analýze.
Minule jsme si řekli, že absolutní hodnota čísla z = a+bi je |z| = sqrt(a2+b2). A abychom se nemuseli pořád tahat s tou odmocninou, definujme si ještě normu N komplexního čísla z takto: N(z)=a2+b2 (norma čísla z je tedy čtverec jeho absolutní hodnoty - to se velmi hodí pokud počítáte s celými čísly). Když si teď definujeme další komplexní číslo w = c+di a spočítáme si součin z*w, dostaneme výraz, jehož struktura se velmi nápadně podobá výše uvedené identitě (!):
z*w = (a+bi) * (c+di) = (ac-bd) + (ad+bc)i
Fibonacciho rovnost si tedy můžeme přepsat pomocí norem:
N(z) * N(w) = N(z*w)
a pokud rovnici odmocníme, dostaneme totéž pro absolutní hodnotu:
|z| * |w| = |z*w|
To mimo jiné znamená, že absolutní hodnota se v komplexních číslech chová přesně jako v reálných (tam je ta poslední rovnice ale triviání): absolutní hodnota součinu je součin absolutních hodnot. To je další náznak, že komplexní čísla jsou právoplatným rozšířením reálného systému. Dokonce se dá ukázat, že i absolutní hodnota podílu dvou komplexních čísel se chová jako její reálný protějšek (důkaz je ale o něco techničtější než formulka přítele Fibonacciho - alespoň Nick Carter to říká):
|z| / |w| = |z/w|
Pro Gaussovská čísla je samozřejmě nejdůležitější ta "normová formulace" . Dává nám totiž návod jak faktorizovat komplexní celá čísla. Norma nám z komplexního monstra udělá přirozené číslo, takže ta Fibonacciho identita de facto funguje jako jakýsi most mezi tajemnými Gaussovskými čísly a nám dobře známými čísly přirozenými. V podstatě nám říká, že pokud se nějaké Gaussovské číslo dá komplexně rozložit na součin, pak se obdobným způsobem dá rozložit i jeho norma.
Podívejme se na konkretní příklad jednoho Gaussovského součinu:
(2+5i) * (1-2i) = 12 + i
Když si teď spočítáme normy jednotlivých aktérů této rovnice, zjistíme, že norma výsledného součinu (pravá strana) je 145, zatímco členy na levé straně mají normu 29 a 5. Ta norma se tedy rozložila přesně podle obou komplexních činitelů: 145 = 29*5.
Teď si také můžeme ukázat, že číslo 3+8i z rozkladu na konci předchozí sekce je skutečně (komplexní) prvočíslo. Kdyby se to číslo totiž dalo napsat jako součin dvou jiných netriviálních čísel
3+8i = Z * W
pak bychom pro jejich normy dostali (podle Fibonacciho)
N(3+8i) = N(Z) * N(W)
Jenže ta první norma je rovna 73 a pokud by takový netriviální rozklad na Z*W skutečně existoval, dostali bychom z norem těch součinitelů N(Z) a N(W) rozklad prvočísla 73 a to není možné. Takže to číslo 3+8i už se dál rozkládat nedá a je to opravdické komplexní prvočíslo. Můžete si zkusit ho ohnout mezi zuby.
(stejně jako v reálném případě, zanedbáváme při rozkladu na prvočinitele čísla s normou 1: což je v komplexním případě 1, -1, i, -i)
Obecně platí, že číslo a+ib (s nenulovými komponentami a,b) je komplexním prvočíslem pokud je jeho norma N(a+ib) reálným prvočíslem. To identifikaci prvočísel v komplexní rovině hodně usnadňuje.
+++++++++
S trochou fantazie můžeme Fibonacciho identitu použít i na faktorizaci komplexních čísel. Zkusme si malý příklad. Jak bychom rozložili na prvočinitele číslo 4+7i? Pokud se dá rozložit na dva menší součinitele W a Z, musí pro ně platit 4+7i = Z * W a pro normy dostaneme z Fibonacciho identity
N(4+7i) = N(Z) * N(W)
To číslo nalevo je ovšem 65 a jediná možná netriviální faktorizace je 5*13 (1*65 nebrat). To znamená, že potřebujeme jedno komplexní číslo jehož norma je 5 a druhé, jehož norma je 13. Z tabulky na konci předchozí sekce vidíme, že normu 5 budou mít čísla 1+2i a 2+i a normu 13 bude mít 2+3i a 3+2i. Všechny ostatní verze dostaneme pronásobením těchto vhodnou jednotkou, např. 1-2i = -i*(2+i). No a teď už ty kandidáty musíme jenom správně zkombinovat. Prakticky orientovaným čtenářům bych opět doporučil metodu pokusů a omylů. Chvíli si s tím budete hrát a za chvíli dostanete správnou kombinaci:
4+7i = (2+i)*(3+2i).
Pokud Vás hádání neuspokojuje, můžete se mrknout sem (a zde je na procvičení tabulka faktorizací pro malá Gaussovská čísla).
Když se na tu identitu podíváme s trochou historického nadhledu, musí nás překvapit, že v době, kdy po Evropě drandili křižáci a nejbohatším Američanem byl náčelník Siouxů, objevil Fibonacci jednak důležitou vlastnost komplexního násobení a jednak nástroj na faktorizaci komplexních čísel. Samozřejmě ve středověku se o komplexních číslech nemluvilo ani v anarchistických kroužcích, takže jeho rovnice byla dlouho považována jen za samoúčelnou matematickou kuriozitu. Teprve po dlouhých 600 letech (!) se vyjevil její pravý význam. Je to jako byste vynalezli hřídel a pak museli 600 let čekat, až k ní někdo dovynalezne kolo. Věda zkrátka není lineární a přestože v učebnicích je úhledně seřazená podle logiky věci, ten skutečný proces objevování je daleko chaotičtější. A kdo ví, třeba za 100 let kápneme na nějaké nové fyzikální paradigma, z jehož pohledu bude řekněme kvantová mechanika tou nejpřirozenější teorií. Zatím mi ale připadá spíš jako náhodně objevená střecha, která sice skvěle funguje, ale stále k ní nemáme čtyři stěny a základy. Tak jako jsme je kdysi neměli pro objev pana Fibonacciho.
+++++++++
Komplexní prvočísla
Teď když jsme se díky příkladné píli dynamického dua F+F trochu zorientovali v Gaussovských číslech, podíváme se jak to má komplexní rovina s prvočísly. Podobně jako v reálném případě, existují tři základní druhy.
Tvrdá prvočísla (3, 7, 11,...) se ani v komplexních číslech rozložit nedají a zůstávají tedy prvočísly sama o sobě. Nalézají se na reálné ose přesně tam, kde je očekáváme: tedy trojka v bodě 3+0i, sedmička v bodě 7+0i, jedenáctka v bodě 11+0i atd. Jejich kopie na ose imaginární jsou také prvočísly: 3i, 7i, 11i atd.
Měkká prvočísla (5, 13, 17,...) se dají rozložit na součin dvou komplexně sdružených čísel (viz závěr první sekce) a sama o sobě přestávají být prvočísly. Jejich úlohu přebírají ty dva komplexně sdružené faktory, které z nich vytřískáme - takže např. 5 se stane složeným číslem a na její místo u prvočíselného dvora nastupují dceřinné deriváty 1+2i a 1-2i (popřípadě 1+2i a 2+i, podle toho jakou konvenci používáte).
Číslo 2 má i v komplexní rovině speciální roli. Samo o sobě prvočíslem není, protože se dá rozložit na 2 = (1+i)*(1-i). Tento rozklad má - na rozdíl od těch předchozích - tu vlastnost, že jeden činitel se dá převést na druhý vynásobením komplexní jednotkou (zde -i)
1-i = -i * (1+i)
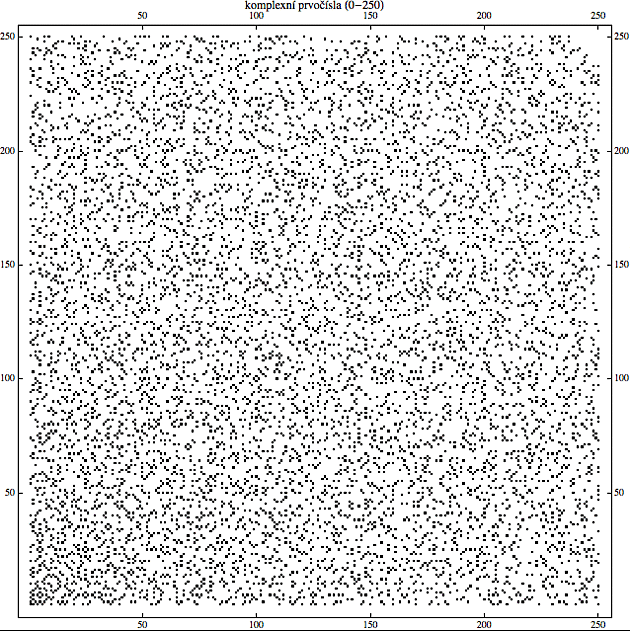
Protože tvrdá prvočísla si určitě pamatujete ze školy, podíváme se, kde v komplexní rovině leží prvočísla, která jsme dostali rozkladem těch měkkých. Ukážu vám ale pouze výřez prvního kvadrantu komplexní roviny v rozmezí 0-50 a to jak pro x, tak pro y (v těch zbývajících kvadrantech je obrázek zcela symetrický). V levém dolním rohu leží číslo 1+i a v pravém horním 50+50i. Tam kde je dané Gausovské číslo a+bi prvočíslem, je příslušný čtvereček vybarven černě.
Takže ta spodní řada (čtena zleva doprava) odpovídá číslům 1+i, 2+i, 3+i... atd. 3+i prvočíslem není a proto je ten třetí čtvereček bílý. Všimněte si, že stejně jako reálná prvočísla se na číselné ose vyskytují náhodně, jsou i tato rozházena po komplexní rovině zcela bez ladu a skladu. Celé generace matematiků se za dlouhých zimních večerů pokoušely rozklíčovat ten předchozí obrázek, ale žádný vzorek nebo zákonitost z něho zatím nikdo nevykoukal.
Další obrázek ukazuje to samé pro větší výřez (od 0 do 250)
(chcete-li ještě větší obrázek, jukněte sem a klikněte na něj)
Všimněte si, že ta čísla jsou po komplexním poli rozsetá jakoby je rozhazoval nějaký farmář: sice nahodile, ale současně s pečlivou rovnoměrností (nenajdete žádný větší kousek komplexní roviny, kde by se žádná prvočísla nevyskytovala). Nemají ovšem stejnou hustotu. V okolí počátku (vlevo dole) je jich o něco více. Je to skoro jako by pánbůh ta prvočísla v komplexní rovině nejprve podle předem připravené hustoty plánovaně a pravidelně rozložil a pak přikvačil ďábel a ta čísla mu trochu rozházel. Do každého náhodně kopnul, takže se posunulo o pár políček tam či onam, čímž se sice jejich celková hustota nezměnila, ale o jejích individuálních pozicích se v důsledku tohoto potměšilého činu nedá nic kloudného říci. Já například vím, že číslo 23+8i je prvočíslo, ale když se mě zeptáte, kolik kroků doprava musím udělat než narazím na další prvočíslo, tak si to musím odkrokovat a prubnout každé číslo metodou pokusů a omylů (žádný algoritmus na to není). Naštěstí to další prvočíslo vpravo je v tomto případě celkem blízko, stačí udělat deset kroků a máte ho: 33+8i.
(zbytek této sekce můžete přeskočit)
Komplexní čísla nám také umožňují pochopit některé vlastnosti reálných čísel. Když se podíváte u toho prvního obrázku na spodní řadu, naleznete na ní následující prvočísla (ve tvaru n+i): 1+i, 2+i, 4+i, 6+i, 10+i, 14+i, 16+i, 20+i, 24+i, 26+i... Ta odpovídají přesně těm hodnotám n, pro které je 1+n2 prvočíslem (to opět vyplývá z Fibonacciho identity). Ten poslední (a stále nevyřešený) problém z prvočíselného Matykání se tedy dá přeformulovat i takto: existuje na té nejspodnější řádce nekonečně mnoho černých čtverečků? A my nevíme. Nikdo to zatím nedokázal ani nevyvrátil.
Pokud si na to Matykání vzpomenete, každým bodem {n,1} se dá vést kružnice (se středem v počátku) a pokud 1+n2 není prvočíslem, tak ta samá kružnice protne ještě další celočíselné body, které musí mít samozřejmě stejný součet čtverců (z Pythagorovy věty). Tady je malá připomínka těch "dalších" celočíselných bodů (a vezmu jen sudá n; pro lichá není možné, aby byl výraz 1+n2 prvočíslem):
1+22 (je prvočíslo)
1+42 (je prvočíslo)
1+62 (je prvočíslo)
1+82 = 42+72 (není prvočíslo)
1+102 (je prvočíslo)
1+122 = 82+92 (není prvočíslo)
1+142 (je prvočíslo)
1+162 (je prvočíslo)
1+182 = 62+172 = 102+152 (není prvočíslo)
1+202 (je prvočíslo)
1+222 = 142+172 (není prvočíslo)
Zvídavého čtenáře jistě napadne, jak se ty "další body" spočítají? V tom prvočíselném Matykání jsem to prostě vykreslil na čtverečkovaný papír a odkud se ty body berou jsem se nestaral. Teď si to ale můžeme říci - ono se to dá odvodit z faktorizace příslušných komplexních čísel.
Tak třeba číslo 8+i se dá rozložit na prvočinitele takto:
(8+i) = (2-i)*(3+2i)
Ale jak teď přijít lacino k dalšímu komplexnímu číslu na té samé kružnici (procházející počátkem)? Jednoduše - stačí objevit další celočíselný bod se stejnou normou. A protože si lehce spočítáme, že čísla komplexně sdružená mají stejnou normu jako jejich originály, vezmeme si daný rozklad, jedno číslo (je jedno které!) změníme na komplexně sdružené (tj. prohodíme znamínko u i) a výsledný součin bude muset mít stejnou absolutní hodnotu (takže příslušný bod bude ležet na stejné kružnici). Tady implicitně opět používáme Fibonacciho identitu.
Já tedy prohodím íčkové znamínko u toho prvního členu:
(2+i)*(3+2i) = 4+7i
Aha, tak odtud se bere ten druhý součet čtverců: 42+72
A pokud má komplexní číslo n+i těch faktorů více, máte více prostoru pro takové kouzlení. Např. 18+i se rozloží na -(1+2i)2(2+3i)=-(1+2i)(1+2i)(2+3i), takže pro to komplexní sdružování dostanete více kandidátů. Zde Vám ty "další" součty čtverců vyjdou dva.
Můžete si sami zkusit je najít a porovnat s tím výčtem nahoře. V prvním případě jsem "sdružil" ten poslední člen, ve druhém ten prostřední.
-(1+2i)(1+2i)(2-3i) = ...
-(1+2i)(1-2i)(2+3i) = ...
Bon appetit!
+++++++++
Pythagorejské trojice - komplexně
Pythagorejské trojice (někdy též pythagorejské trojúhelníky) jsou trojice přirozených čísel (a,b,c), které odpovídají stranám pravoúhlého trojúhelníka (tj. splňují Pythagorovu větu):
a2+b2 = c2 (např. 32+42 = 52)
Jak jméno napovídá, tyto trojice byly známy již starým Řekům a přestože jich existuje nekonečně mnoho, dají se poměrně snadno zmapovat. Tady je prvních sedm.
| (3,4,5) | (5,12,13) | (8,15,17) | (7,24,25) | (20,21,29) | (12,35,37) | (9,40,41) |
|---|
Pokud vynásobíme takovou trojici přirozeným číslem, dostaneme další pythagorejské trojúhelníky, ale ty budou mít strany obsahující společného dělitele. Např. z (3,4,5) dostaneme (6,8,10), (9,12,15) atd. Těm původním trojúhelníkům, jejichž strany jsou nesoudělné, říkáme primitivní a ty nás samozřejmě zajímají nejvíce. Ty vynásobené už pak zvládne každý žák základní školy.
Podívejme se teď na kopii kousku komplexní roviny, ve které jsem černou tečkou vyznačil Gaussovská čísla (tj. reálná i imaginární složka je celé číslo).
Na první pohled je jasné, že tu na nás pomrkává celá spousta pravoúhlých trojúhelníků. Stačí si vzít libovolný bod (na obrázku 4+7i), spustit kolmici a máme hnedle trojúhelník s celočíselnými odvěsnami (zelená svisle a modrá vodorovně).
Problém je s přeponou. Ta červená měří sqrt(65) a to bohužel není celé číslo. My bychom potřebovali tu přeponu nějak umocnit na druhou. A z diskuse Fibbonaciho identity vyplývá, jak na to. Pro komplexní čísla totiž platí, že absolutní hodnota čtverce je čtverec absolutní hodnoty (v té rovnici pro absolutní hodnoty z Fibonacciho sekce prostě položíte w=z):
|z2| = |z|2
Pokud se nám tedy v absolutní hodnotě (přepona) plete pod nohy nějaká zatracená odmocnina (sqrt), zbavíme se jí tak, že dané komplexní číslo umocníme na druhou a ten čtverec pak tu odmocninu sežere.
Umocněme tedy naše číslo na druhou:
(4+7i)2 = (4+7i)*(4+7i) = -33 + 56i
a po krátkém výpočtu s kalkulačkou vidíme, že absolutní hodnota tohoto čísla je 65 (je to čtverec té předchozí: sqrt(65)). A je to! Pouhým komplexním čtvercem jsme získali pythagorejskou trojici: (33,56,65). Na případné mínusy zde nehleďte. Ty nám jen říkají, zda náš trojúhelník trčí v soustavě souřadné doprava nebo doleva, popřípadě dolů.
A tohle platí zcela obecně pro jakékoliv Gaussovské číslo. Jakmile spočítáte jeho čtverec, máte okamžitě dvě odvěsny budoucího pythagorejského trojúhelníka. A přeponu pak lehce dopočítáte. V následujících příkladech vám tu přeponu ukážu v závorce napravo (aby ty trojúhelníky byly lépe vidět):
(1+2i)2 = -3 + 4i (5)
(2+3i)2 = -5 + 12i (13)
(1+4i)2 = -15 + 8i (17)
(3+4i)2 = -7 + 24i (25)
A takto si postupně nabrnkáte všechny primitivní pythagorejské trojice. A nebojte se, Gaussovských čísel je nekonečně mnoho, takže na každého zbyde.
Záměrně jsem vynechal číslo 1+3i. Pokud jsou obě komponenty liché, nedostanete nic nového, jen dvojnásobek už objevené trojice. Počítejte se mnou:
(1+3i)2 = -8 + 6i (10)
a to je de facto dvojnásobek trojúhelníka (3,4,5) s prohozenými odvěsnami. Pokud této záhadě chcete příjít na kloub, zkuste experimentovat s číslem x+iy, kde jsou obě komponenty liché, a pak s číslem X+iY, jehož komponenty budou
X = (y-x)/2
Y = (y+x)/2
Uvidíte, že dostanete podobné trojúhelníky.
+++++++++
Abychom si mohli odvodit obecný vzoreček pro Pythagorejské trojice, spočítáme si čtverec obecného Gaussovského čísla
(x+iy)2 = (x+iy) * (x+iy) = (x2-y2) + 2xyi
Tím máme odvěsny a absolutní hodnota nám opět vyjeví přeponu, která se po chvíli úmorného počítání vyloupne ve tvaru x2+y2. No a když si to komplexní číslo x+iy představíme jako dvojici čísel, vyjde nám slavná parametrizace pythagorejských trojic (tedy formulka, která nám říká, jak z daných libovolně zvolených parametrů x,y vydundat trojici (a,b,c)):
{x,y} --> (x2-y2,2xy,x2+y2)
A dalších parametrizací existuje celá řada (viz zde a nebo zde).
+++++++++
Pythagorejské trojice - reálně
Pro ty, kdo už si stačili na komplexní čísla vytvořit alergii, mám dobrou zprávu. Ty pythagorejské trojice se dají nasekat i s pomocí reálných čísel, ale trochu si u toho započítáme (už to nebudou jen čtverce Gaussovských čísel). Takže na chvíli zapomeňte na všechna ta íčka a jdeme na to reálně.
Východiskem nám bude středoškolská geometrie - konkretně jednotková kružnici x2+y2 = 1 a rozložení racionálních bodů na ní. To jsou body jejichž obě souřadnice jsou zlomky.
Nejprve si uvědomíme, že pokud na té kružnici leží racionální bod, tak obě jeho komponenty musí mít stejného jmenovatele: vezměme si takový bod {a/b,c/d} a předpokládejme, že oba zlomky jsou už v základním tvaru, tj. neobsahují žádné společné dělitele. Z rovnice kružnice dostaneme:
(a/b)2+(c/d)2 = 1
a obě strany pak vynásobíme součinem jmenovatelů na druhou (bd)2:
(ad)2+(bc)2 = (bd)2
Protože poslední dva členy obsahují b2, musí b2 dělit i první člen. Ale a a b jsou nesoudělná, takže b musí dělit d. Obdobně vidíme, že oba krajní členy obsahují d2, takže d2 musí dělit i prostřední člen. Ale d a c jsou opět nesoudělná, takže d musí dělit b. A pokud d dělí b a současně b dělí d, musí být obě čísla stejná. Quod erat demonstrandum.
+++++++++
Teď když víme, že racionální body na kružnici mají stejného jmenovatele v obou souřadnicích, je jejich souvislost s pythagorejskými trojicemi nabíledni. Vezměme si jeden takový racionální bod na kružnici a napišme si jeho rovnici (c bude ten společný jmenovatel):
(a/c)2+(b/c)2 = 1
Teď tu rovnici pronásobíme c2 a máme rázem pythagorejskou trojici:
a2+b2 = c2
A naopak to funguje podobně. Máme-li trojici (a,b,c), splňující výše uvedenou rovnici, vydělíme ji c2 a rázem máme racionální bod na kružnici. Mezi racionálními body na kružnici a pythagorejskými trojicemi je tedy velmi úzký a přesně definovaný vztah. To nám ovšem ještě neříká, kde na kružnici ty racionální body hledat (a jen tak si na ose x náhodně vybrat nějaký zlomek a pak zkusit dopočítat y k cíli většinou nevede). Za tímto účelem si musíme udělat následující chytrou konstrukci (viz obrázek).
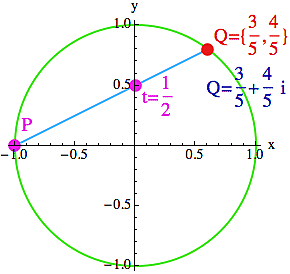
Uvažujme modrou přímku procházející jednak bodem P={-1,0} a jednak bodem {0,t} na ose y, kde t je nějaké racionální číslo. Na obrázku je t=1/2. Tato přímka protíná kružnici ve dvou bodech. Jeden známe - to je P - a ten druhý, Q, si dopočítáme.
Jak to uděláme? Spočítáme rovnici té modré přímky a dosadíme ji do rovnice kružnice (protože chceme najít bod té přímky, který tu rovnici kružnice splňuje). Směrnice přímky je tangens jejího úhlu, což je v našem případě t/1. A rovnice přímky, která prochází bodem P a má směrnici t je:
y = t*(1+x)
Když v rovnici kružnice převedeme x2 na druhou stranu a za y dosadíme výše spočítaný výraz, dostaneme:
t2*(1+x)2 = 1-x2
Protože 1-x2 = (1+x)*(1-x), můžeme (1+x) v rovnici zkrátit (tento člen nám beztak dává jen průsečík, který už známe, tj. x=-1) a dostaneme konečnou rovnici pro x:
t2*(1+x) = 1-x
no a z ní už snadno spočítáme x:
x = (1-t2) / (1+t2)
Z výše uvedené rovnice pro y pak lehce dopočítáme
y = 2t / (1+t2)
a tím máme bod Q spočítaný (v závislosti na t). A protože t je zlomek, napíšeme ho jako t = m/n a dostaneme konečnou podobu racionálního bodu Q:
Q = {(1-t2) / (1+t2), 2t / (1+t2)} = {(n2-m2) / (n2+m2), 2mn / (n2+m2)}
Takovému bodu pak odpovídá - podle diskuse na začátku této sekce - následující pythagorejská trojice parametrizovaná celými čísly m,n:
{m,n} --> (n2-m2, 2mn, n2+m2)
Vidíte, že je to prakticky stejné řešení jako parametrizace na konci sekce předchozí, až na volbu písmenek. Pokud si vyberete řekněme {m,n} = {1,2}, lehce si spočítáte, že odpovídající pythagorejský trojúhelník je (22-12, 2*2*1, 22+12) = (3,4,5). To je ten základní. No a ty další si nabrnkáte jinou volbou dvojice {m,n}.
Tato konstrukce nám tedy přesně spárovala všechna racionální čísla na ose y s racionálními body na kružnici. Je to jako bychom z bodu P prosvítili osu y modrým laserovým paprskem a podívali se, kam na naší kružnici dopadne. A kdykoliv ten paprsek prochází racionálním číslem (na ose y), jeho obraz na jednotkové kružnici bude racionální bod. Každé racionální číslo (dvojice m,n) nám tedy vykouzlí jednu pythagorejskou trojici (takovým bodem určenou).
+++++++++
Na první pohled se zdá, že jsme se v této konstrukci komplexním číslům úspěšně vyhnuli (i když jsme zpocení jak dveře od chlíva). Ale ony na nás ve skutečnosti šibalsky vykukují i zpoza té jednotkové kružnice.
Racionální body na jednotkové kružnici si totiž také můžeme představit jako komplexní čísla (to je ta modrá formulka na ilustračním obrázku). Pojďme si rychle rozmyslet, jak bychom taková komplexní čísla dostali. V první řadě by to měly být podíly Gaussovských celých čísel, řekněme Z/W, protože hledáme racionální body. A v druhé řadě by ta čísla W a Z měla mít stejnou absolutní hodnotu, protože chceme, aby jejich podíl ležel na jednotkové kružnici (všechny její body mají absolutní hodnotu 1):
|Z / W| = |Z| / |W| = 1
Jak takové číslo W (pro dané Z) najdeme už asi tušíte. Bude to číslo komplexně sdružené, tedy Z*. To má stejnou absolutní hodnotu jako Z. Takže my si ty racionální body na kružnici můžeme spočítat daleko rychleji jako podíly komplexních čísel Z/Z*, kde Z je libovolné Gaussovské číslo.
Tak schválně: co dostaneme jako podíl (2+i) / (2-i)?
Jak jsme si řekli minule, při počítání podílu rozšíříme celý zlomek číslem komplexně sdruženým (ke jmenovateli) a v tomto případě dostaneme
(2+i) / (2-i) = (2+i)*(2+i) / (2-i)*(2+i) = (2+i)2 / 5 = (3+4i)/5
No vida. A máme ten bod Q zcela bezbolestně. Není třeba nic řešit. A všechny ostatní racionální body na kružnici dostaneme z podílu Z/Z* pro ostatní Gaussovská čísla. Zase tak úplně překvapující to ale není. Jak zlomek t=m/n, tak Gaussovské číslo Z=m+in, v podstatě reprezentují pár celých čísel {m,n} a zda si pro konstrukci těch racionálních bodů vyberete podíly komplexně sdružených čísel a nebo zlomky, prosvícené tím modrým laserovým paprskem, záleží jen na tom, zda jste Gaussofob a nebo zlomkofob.
Mimochodem, když si dobře prohlédnete závěr té poslední rovnice, vidíte, že tam na vás urputně mává i čtverec komplexního čísla, přesně ten samý čtverec, který hrál v předchozí sekci hlavní roli. A ta pětka ve jmenovateli už ten čtverec pouze dopraví na jednotkovou kružnici (číslo (2+i)2 samo o sobě sedí na kružnici s poloměrem 5).
A jsme v cíli. Ufff.
Takže abych to dnešní Matykání nějak kulantně shrnul: pythagorejské trojúhelniky jsou vlastně komplexní čtverce na jednotkové kružnici. A kdo z toho ješte stále není jelen, nechť se přihlásí o přestávce v ředitelně.
+++++++++
Na uklidněnou pokračujeme v české sérii. A protože je léto, vybral jsem jednu starou písničku s letním motivem. Lilka Ročáková: Bylo léto, horké léto.
Předchozí díly Matykání.
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
| Další články autora |
Tři roky vězení. Soud Ferimu potvrdil trest za znásilnění, odvolání zamítl
Městský soud v Praze potvrdil tříletý trest bývalému poslanci Dominiku Ferimu. Za znásilnění a...
Moderní lichváři připravují o bydlení dlužníky i jejich příbuzné. Trik je snadný
Premium Potřebujete rychle peníze, pár set tisíc korun a ta nabídka zní lákavě: do 24 hodin máte peníze na...
Takhle se mě dotýkal jen gynekolog. Fanynky PSG si stěžují na obtěžování
Mnoho žen si po úterním fotbalovém utkání mezi PSG a Barcelonou postěžovalo na obtěžování ze strany...
Školu neznaly, myly se v potoce. Živořící děti v Hluboké vysvobodili až strážníci
Otřesný případ odhalili strážníci z Hluboké nad Vltavou na Českobudějovicku. Při jedné z kontrol...
Prezident Petr Pavel se zranil v obličeji při střelbě ve zbrojovce
Prezident Petr Pavel se při střelbě na střelnici v uherskobrodské České zbrojovce, kam zavítal...
Nejednáme. Na obzoru je stávka soudních pracovníků, požadují vyšší platy
Premium Odvádějí vysoce odbornou práci, musejí skládat speciální zkoušky, někdy sami vypracovávají drobná...
Pokroková nenávist k Židům. Jak se z univerzit v USA staly filiálky Hamásu
Premium Na elitních amerických univerzitách vyhánějí Židy takovým stylem, že to tam vypadá jako v Německu...
Karafiátovou revoluci zažehla jediná píseň. Portugalsko vyvedla z diktatury
Málokterá revoluce je spojena s písní a květinou, jako se to stalo té portugalské. Před 50 lety se...
Chtěl se odpálit během olympiády v Paříži. Ve Francii zatkli 16letého hocha
Kriminalisté ve Francii v úterý zadrželi 16letého mladíka francouzské národnosti, který na...

Byt 3+1, družstevní, 73 m2
Cajthamlova, Teplice
2 100 000 Kč
- Počet článků 402
- Celková karma 19,54
- Průměrná čtenost 920x