Matykání: Naši Fourianti

Tak jako se běžné funkce dají rozložit na nekonečné kombinace mocnin, periodické funkce se dají rozložit na kombinace sínů a kosínů. Jejich studium nás dovede až k zajímavé interpretaci Heisenbergova principu neurčitosti.

"Historie se opakuje", tvrdí klasik.

A touto otřepanou hláškou jen potvrzuje pradávné zkušenosti našich předků. Život na této planetě má pozoruhodnou zálibu v cyklech. Od kmitání atomů, přes čtvero ročních období či pravidelné střídání ekonomické expanze a deprese až po - řečeno s Cimrmanem - "periodicky se opakující měsíční dny nervozity a hysterie".

Z pohledu matematiky jsou opakující se děje popsány periodickými funkcemi. Představíme-li si nezávisle proměnou jako čas a délku cyklu (periodu) označíme písmenkem p, pak tyto funkce splňují poměrně jednoduchou podmínku:

f(x+p) = f(x) pro každé reálné x

tj. po uplynutí času p se funkce vrátí do výchozí pozice a její průběh se začne opakovat.

+++++++++

Lidstvo je odnepaměti posedlé touhou rozkládat věci na elementární kousíčky. Od skládačky Lega, přes vyjádření vektorů pomocí báze až po rozklad hmoty na elementární částice. Dá-li se něco rozmontovat, nějaký kutil to dříve nebo později učiní.

Notoričtí rozkládači samozřejmě tušili, že i funkce periodické by se měly dát rozložit na nějaké elementárnější stavební kameny, ze kterých by se ty komplikovanější mohly sestavit.

A co je elementárnějšího než síny a kosíny, které v zásadě popisují obíhání bodu po kružnici - tedy jeden z nejjednodušších periodických procesů.

Věda zabývající se rozkladem periodických dějů se jmenuje harmonická analýza a protože lví podíl na jejím rozvoji má praotec fouriant, tj. francouzský matematik Joseph Fourier, říká se jí také někdy Fourierova analýza (obvykle v kontextu goniometrických funkcí).

Vzhledem k tomu, že kombinace sínů a kosínů s celočíselnými násobky periody jsou v zásadě trigonometrické polynomy, de facto dnes navážeme na Matykání o nekonečných polynomech.

+++++++++

Základní perioda

V celé této sekci bude platit, že p=2? (alias 360°).

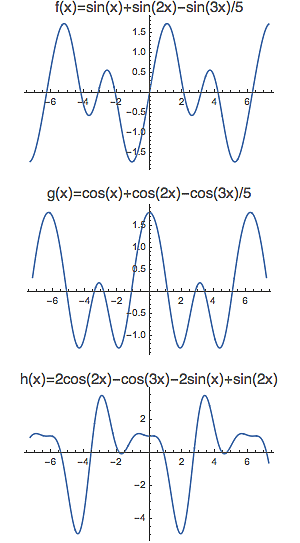
Začneme pohledem na klasický graf funkcí sínus a kosínus. Obě mají periodu p a to znamená, že jakmile známe tyto funkce na libovolném intervalu délky p, známe je všude, protože na zbytku číselné osy se jejich hodnoty dají dopočítat z periodického vztahu f(x+p)=f(x). Za zmínku stojí také skutečnost, že funkce kosínus je pouze fázovým posunutím funkce sínus - tj. její graf obdržíme "šoupnutím" sínu o hodnotu ?/2, neboli o 90° (horní obrázek).

Pokud budeme nezávisle proměnnou x násobit přirozenými čísly, graf funkce kosínus začne kmitat rychleji a rychleji, jak je vidět ve spodní části obrázku.

Funkce f(x)=cos(2x) má periodu pouze p/2, což je lehce vidět z toho, že

f(x+p/2) = cos(2(x+p/2)) = cos(2x+p) = cos(2x) = f(x)

(předposlední rovnítko plyne z toho, že sin(x) má periodu p)

Funkce cos(3x) má analogicky periodu p/3 a stejně to funguje pro další celočíselné násobky. Funkce sin(kx) má tedy periodu k-krát menší (p/k), protože kmitá s k-krát větší frekvencí f = 1/p.

Funkce s periodou p je pochopitelně periodická také s periodou 2p, 3p, 4p,...   (tedy libovolný přirozený násobek p). Aby nevznikl chaos, tak se té nejmenší (základní) periodě říká primitivní perioda.

Z toho vyplývá, že funkce sin(x), sin(2x), sin(3x), sin(4x), ... cos(x), cos(2x), cos(3x), cos(4x),... mají všechny periodu p (byť ne nutně primitivní) a to nám umožní je kombinovat a nevypadnout při tom z množiny p-periodických funkcí.

Dohromady budu tomuto ánsámblu říkat bázové funkce, protože právě z nich budeme skládat všechny p-periodické děje.  K nim ještě přihodím konstantní funkci f(x)=1, neboť i ona má (triviálně) periodu p a můžeme si ji představovat jako funkci f(x) = cos(0x), aby "vypadala stejně".

A podobně jako si v lineárním prostoru můžeme všechny vektory nabrnkat pomocí lineárních kombinací bázových vektorů, můžeme si i všechny rozumné p-periodické funkce nabrnkat kombinováním výše uvedených sínů a kosínů. Ty vysokofrekvenční funkce nám de facto umožňují "dotvářet" tvar naší periodické funkce uvnitř periody (jen základní oblouček sínu by sám o sobě různé komplikované p-periodické děje popsat nedokázal).

Podívejme se tedy, co nám to kombinování přinese.

Uvažujme například funkce f(x) = sin(x) + sin(2x) - sin(3x)/5 a g(x) = cos(x) + cos(2x) - cos(3x)/5.

Na obrázku vpravo vidíme, že funkce f bude lichá (protože věechny ty síny jsou liché), zatímco funkce g bude z podobného důvodu sudá. Pochopitelně můžeme ty síny a kosíny různě splácat dohromady (spodní část obrázku) a pak ta výsledná funkce nebude ani lichá ani sudá. Obě ale budou stále periodické s periodou p, protože všechny bázové funkce jsou p-periodické.

Vidíme, že i jednoduchými kombinacemi sínů a kosínů si můžeme našlehat funkce s poměrně komplikovaným chováním.

Fourierova analýza se v podstatě zabývá obráceným problémem.

Když vám našlehám nějakou komplikovanou p-periodickou funkci f(x), dokážete poznat či spočítat z jaké konkretní kombinace sínů a kosínů tato funkce vznikla?

+++++++++

Touto otázkou už jsme se v minulosti potýkali (v této sekci Jauvajs), takže jen stručné shrnutí.

Na bázové funkce sin(x), sin(2x),...a jejich kosínové ekvivalenty se díváme jako na bázové vektory nekonečně rozměrného prostoru funkcí a hledaná kombinace bázových funkcí, která nám vytvoří danou funkci f(x) se najde úplně stejně, jako když v 3D hledáme kombinaci bázových vektorů e1, e2, e3 která dokáže vygenerovat daný vektor u.

Výsledek se spočítá projekcí - tj. složky hledané kombinace jsou prostě projekce vektoru u do vektorů e1, e2, e3. S funkcemi to funguje úplně stejně (koneckonců prostor funkcí je vektorový prostor jako každý jiný - jen má nekonečnou dimenzi).

Takže pro danou p-peridickou funkci hledáme rozvoj

(+) f(x) = a0 + a1 cos(x) + a2 cos(2x) + a3 cos(3x) + ... + b1 sin(x) + b2 sin(2x) + b3 sin(3x) + ...

s tím, že všechny koeficienty an a bn jsou prostě projekcemi zadané funkce f do naznačených bázových funkcí

a0 = c ?f(x)dx
an = c ?f(x)cos(nx)dx
bn = c ?f(x)sin(nx)dx

(integrujeme přes interval délky p a normalizační konstanta má hodnotu c = 1/?)

Je to úplně stejná mechanika, jako pro rozklad vektoru, jen musíte mít na zřeteli, že skalární součin je v prostoru funkcí definován integrálem (spojitým součtem) přes všechny hodnoty x a ne součtem běžným (diskrétním) přes všechny hodnoty indexu i. Pokud tuto analogii chcete dokonale vstřebat, dívejte se na nezávisle proměnnou x jako na "index složek" dané funkce a nebo se naopak na 3D vektor (x,y,z) dívejte jako na funkci, která zobrazuje indexy na komponenty: 1-->x, 2-->y a 3-->z.

Protože všechny bázové funkce jsou ortogonální (což se musí pracně ověřit integrací skalárních součinů!) a tvoří tzv. úplný systém (což přenecháme k ověření koňovi), výše popsané formulky nám umožní rozložit každou rozumnou funkci f(x).

Např. Fourierovým rozkladem funkce g(x) z předchozího obrázku získáme nazpátek její definici:

g(x) = cos(x) + cos(2x) - cos(3x)/5

tedy a1=1, a2=1 a a3=-1/5 a všechny ostatní koeficienty budou nula (ani to nemusíte integrovat - opět je to vidět z ortogonality). Tady jsme se samozřejmě pouze dozvěděli, že funkce má přesně ty frekvenční složky, které jsme do ní vložili. Obecně ale funkce může být vyjádřena jinak (než kombinací goniometrických funkcí) a těch nenulových koeficientů může být nekonečně mnoho (tedy k popsání všech detailů funkce f bychom potřebovali nekonečně mnoho těch vysokofrekvenčních komponent).

Protože výpočet za nás většinou udělá počítač, důležitá je interpretace.

Ty koeficienty u sínů a kosínů nám v podstatě ukazují, z jakých frekvenčních složek je daná periodická funkce vybudovaná a jak silnou váhu jednotlivé složky mají. Obyčejná sinusoida je složena pouze z jedné frekvenční složky (té základní f=1/2?). Naše funkce g(x) je složená ze tří frekvenčních komponent (cosx, cos2x a cos3x) s frekvencemi (f, 2f a 3f) a s váhami 1, 1 a -1/5.

Pokud je signál naměřený (a není tedy zadaný žádnou formulkou), je nutno všechny integrace provést numericky.

+++++++++

Zatím jsme tiše předpokládali, že funkce f (jejíž Fourierův rozvoj zkoumáme) je p-periodická na celé reálné ose. V praxi nás ale většinou pro konkrétní (ne nutně periodickou) funkci f zajímá pouze poměrně omezený obor hodnot x a v takovém případě se funkce f dá lehce periodicky rozšířit z nějakého malého intervalu (který nás zajímá) na periodickou funkci, definovanou na celé reálné ose. A na ni potom můžeme aplikovat Fourierovu analýzu.

Prož bychom takovou ptákovinu dělali? Protože aproximace funkcí trigonometrickými polynomy dokáže odhalit některé souvztažnosti, které bychom jinými analytickými metodami nezískali.

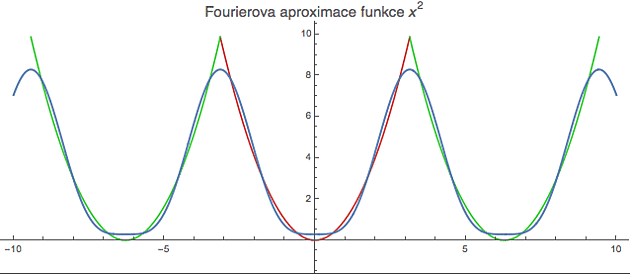
Podívejme se třeba  na klasickou kvadratickou parabolu f(x) = x2 a předpokládejme, že nás budou zajímat pouze hodnoty v okolí nuly (pro určitost řekněme, že |x|<1). Tento interval se v pohodě "vejde" do základního intervalu (-?,?), na kterém si funkci vykreslíme červeně (obrázek dole). Protože chování kvadratické funkce mimo základní interval nás nezajímá, nebudeme se žinýrovat a funkci f(x) vně tohoto intevalu rozšíříme tak, že ten červený kousek paraboly periodicky zkopírujeme (doslova ho pomocí zelených vánočních formiček "přetiskneme" na zbytek reálné osy).

A teď začneme vzniklou periodickou příšerku fourierovsky aproximovat.

Protože naše nasekaná funkce je sudá, budou nás zajímat pouze koeficienty rozvoje do kosínů. Pokud si vezmeme první tři, dostaneme z výše uvedených integrálních formulek

an = (1/?)  ? f(x)cos(nx)dx

(integrujeme od -? do ?)

tuto aproximaci

f(x) ~ 2?2/3 - 4 cos(x) + cos(2x)

Na obrázku ji vidíte v modrém. Vidíte, že pouhé dva kosíny a jedna uňamtaná konstanta dokáží periodicky rozšířenou kvadratickou parabolu aproximovat poměrně obstojně. A pokud přihodíte další člen

f(x) ~ 2?2/3 - 4 cos(x) + cos(2x) - 4 cos(3x)/9

bude aproximace ještě přesnější (tu si vykreslete sami).

Stejně jako u Taylorova rozvoje platí, že čím více členů spočítáte, tím budete mít přesnější aproximaci. A pokud je vezmete všechny (nekonečně mnoho), dostanete přesné vyjádření periodické funkce pomocí Fourierovy řady.

+++++++++

Tohoto triku s periodickým rozšířením původně neperiodické funkce se velmi často využívá při vyčíslování součtu nekonečných řad. Vezme se nějaká rozumná elementární funkce, osekne se, aby se vešla do základního intervalu, pak se periodicky rozšíří a spočítá se její Fourierův rozvoj (+).

Nakonec se dosazením vhodně zvolené hodnoty x získá na pravé straně číslo (funkční hodnota té rozumné elementární funkce) a na straně druhé dostaneme nekonečnou číselnou řadu (do všech sínů a kosínů dosadíme tu vhodně zvolenou hodnotu x).

Koho zajímají krvavé detaily tohoto postupu, může se podívat sem (a nebo sem, kde se místo sínů a kosínů používají komplexní exponenciely).

+++++++++

Obecná perioda

V reálném světě pochopitelně nemůžeme očekávat, že všechny periodické děje budou probíhat s periodou p=2?.

To by tak hrálo, aby si kdejaký matematik stěžoval, že se Zeměkoule otáčí příliš pomalu a jemu pak nevychází Fourierovy koeficienty.

Změna periody ale žádný problém nepředstavuje. Osa x se prostě přeškáluje tak, aby všeliké to kmitání vyšlo správně (něco jako změna jednotek z kilometrů na míle).

Máme-li tedy P-periodickou funkci

f(x+P) = f(x)

pak budeme rozkládat do "přeškálovaných" sínů a kosínů:

sin(nx(2?/P)),cos(nx(2?/P))

(ten člen ve vnitřní závorce je přeškálovací koeficient, který - coby jednička - vypadne, pokud je perioda P = 2?)

Koeficienty rozvoje P-periodické funkce do těchto "přeškálovaných" bázových funkcí se spočítají úplně stejně - tedy z odpovídajících skalárních součinů. Jen v těch skalárních součinech nebudeme integrovat přes interval délky 2?, ale přes interval délky P (a samozřejmě se musí příslušně upravit všechny normalizační konstanty - včetně Husákova vytleskávacího čísla). Kdo se v tom chce trochu láskyplně porochňat, může se mrknout sem (je to popsáno pro periodu P=2L).

Obecná perioda nám umožní studovat frekvenční komponenty všech periodických dějů. A pokud v tom příkladu s rozvojem f(x) = x2 budeme potřebovat nějaký širší interval, např. |x|<10, nebude to žádný problém - prostě funkci rozvineme do "přeškálovaných" bázových funkcí s periodou P=10 (tady je ten samý příklad s periodou P=2).

+++++++++

Ty "přeškálované" bázové funkce mají periody P, P/2, P/3,... a to znamená, že reprezentují frekvence f=1/P, 2f, 3f,... atd.

Stejně jako v předchozí sekci, každý Fourierův koeficient reprezentuje váhu příslušného sínu či kosínu, poslušně kmitajícího v určitém celočíselném násobku té základní frekvence f. Na celé spektrum těchto koeficientů tedy můžeme pohlížet jako na frekvenční reprezentaci konkretního časového signálu (x představuje čas), který se do těch přeškálovaných (ko)sínů rozloží.

Ty fourierovské koeficienty (tedy váhy jednotlivých bázových funkcí), ale nemohou být jen tak nějaká čísla, vytažená z klobouku.  Dá se ukázat, že pro slušně vychované funkce ty koeficienty musí konvergovat k nule pro n blížící se nekonečnu. Váhy vysokofrekvenčních komponent se tedy musí zmenšovat. Wikipedie má hezkou tabulku Fourierových koeficientů pro základní typy funkcí.

Stejně jako v první sekci platí, že Fourierův rozvoj obsahuje pouze celočíselné násobky základní frekvence f. A to znamená, že při kombinování dvou signálů g(x) a h(x) s různými periodami P a Q musíme být opatrní.

Pokud se stane, že dvě periody P a Q jsou racionálně souměřitelné, tj. jejich podíl je zlomek P/Q = p/q (kde p a q jsou celá čísla), pak to znamená, že qP = pQ a oba signály lze v jistém smyslu převést na "společného jmenovatele", což zde bude výše naznačený násobek obou period. Můžeme si je tedy představit jako signály s o něco delší, ale společnou periodou pQ = qP. A tato společná perioda bude periodou kombinovaného signálu (podrobněji zde).

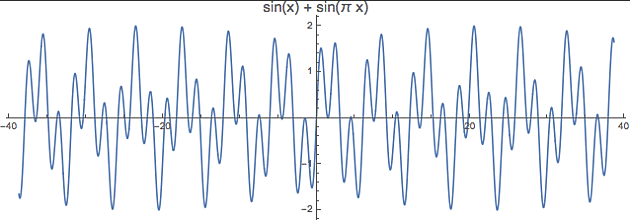
Pokud periody P a Q racionálně souměřitelné nejsou, např. P=2 a Q=2?, pak kombinace obou signálů periodická nebude vůbec (viz další obrázek)

Tady už se společný násobek obou period najít nedá. Kdyby pro nějaká celá čísla platilo, že p1 = q?, tak by ? = p/q bylo racionální číslo (což není!).

+++++++++

Závěrem této sekce malou technickou poznámku.

To, že člověk musí při Fourierově analýze neustále žonglovat jak se síny, tak s kosíny je nepohodlné. Proto si matematici vypomohli komplexní exponencielou, která v sobě zahrnuje oba typy funkcí prostřednictvím vztahu

exp(ix) = cos(x) + i sin(x)

a z něho se dá vyjádřit jak sínus, tak kosínus

sin(x) = (exp(ix) - exp(-ix))/2i
cos(x) = (exp(ix) + exp(-ix))/2

Tím pádem místo komplikovaného vztahu (+) z první sekce dostaneme

(++) f(x) = ? cn exp(inx(2?/P))

kde n probíhá od -? do ? a koeficienty cn jsou komplexní čísla, která se najdou opět prostřednictvím poměrně zapařených integrálů. Koeficient c0 reprezentuje konstantní člen, zatímco ty ostatní představují v párech (cn a c(-n)) jednotlivé frekvenční komponenty. Z těch párů se pak dají vyždímat odpovídající síny a kosíny. Pokud je funkce reálná f, pak ty komplexní koeficienty pochopitelně musí splňovat určité vztahy, aby se imaginární komponenty vyrušily (podrobnosti zde). Ale s tím si nebudeme lámat hlavu.

Díky tomu, že koeficienty cn jsou indexované od -? do ?, tak se dají poměrně dobře vykreslit (pro klasické řady dostanete dvě skupiny koeficientů indexované od 1 do ?, což se vykresluje daleko hůře).

Zdůraznil bych, že na ose x je frekvence. Ty červené body ukazují jednotlivé hodnoty frekvence zastoupené v signálu, zatímco modré hodnoty ukazují jejich váhy (Fourierovy koeficienty). Proto konvergují k nule.

Takový obrázek tedy ukazuje "portrét" dané funkce ve frekvenční doméně, zatímco originální obrázek signálu (např. ten v první sekci), kdy je na ose x čas, reprezentuje funkci v časové doméně. Portrét periodické funkce v časové doméně je spojitý (nezávisle proměnná x nabývá všechny možné hodnoty), portrét ve frekvenční doméně je diskrétní. Periodicita nutí Fourierovy koeficienty daného rozvoje "sedět" pouze v celočíselných násobcích základní frekvence f.

To se změní pokud začneme uvažovat nekonečné periody - což je taková poetická zkratka pro neperiodické funkce (neb si celou reálnou osu můžeme představit jako jednu periodu, uvnitř které si funkce může dělat, co chce).

+++++++++

Nekonečná perioda

Pokud budeme tu základní periodu P zvětšovat nade všechny meze, bude se základní frekvence f=1/P zmenšovat k nule. A to znamená, že ta červená sekvence frekvencí z předchozího obrázku se bude stahovat k nule (bude tedy hustější a hustější) a v limitním případě "vyplní" celou reálnou osu. A to je v podstatě přechod od Fourierovy řady k Fourierově transformaci, který nám umožní analýzu neperiodických funkcí (nebo chcete-li funkcí s periodou P=?). 

Jak jsme viděli, pro konečné periody P je frekvenční spektrum diskrétní (funkce obsahuje pouze násobky základní frekvence f) a váhové hodnoty (tedy Fourierovy koeficienty) pak ukazují podíly jednotlivých frekvencí. Spočítají se podle standardních formulek, které najdete v učebnici, na Internetu či vyškrábané hřebíkem v kóji pánského WC na matfyzu (hned vedle vzorečku pro výpočet obsahu kosočtverce).

Pro nekonečné periody už se v té funkci vezou všechny frekvence (kvůli tomu funkce ztratila svoji periodicitu), takže frekvenční spektrum je spojité (vyplňuje celou reálnou osu) a na příslušné koeficienty se proto můžeme dívat jako na funkci. Každé reálné hodnotě frekvence ? - bez ohledu na to zda je nebo není násobkem nějaké základní frekvence -  odpovídá určitá "váha", tj. kolik této frekvence v naší funkci je. Tu váhu budu pro danou funkci f a danou frekvenci ? značit symbolem f°(?) (jelikož tu nevidím klasickou stříšku nad f). Této sekundární funkci f° (odvozené z f) se říká Fourierova transformace. Ta tedy frekvencím ? přiřazuje jejich váhy f°(?) v signálu f. Schematicky:

f°: ? --> f°(?)

Na první pohled ta Fourierova transformace f° vypadá stejně jako funkce f. Je to prostě určitá funkce v jedné proměnné. Musíme mít ale na paměti, že zatímco signální funkce f operuje v časové doméně (pro každý čas x ukazuje, jak silný zde signál je), její Fourierova transformace f° operuje ve frekvenční doméně (pro každou frekvenci ? ukazuje její podíl v signálu f).

Fourierova transformace (ne nutně periodické) funkce f se definuje pomocí integrálu

f°(?) = ? f(x) exp(-2?i?x)dx

a původní funkce f se pak "složí" z frekvenčního obrazu f° nazpátek pomocí inverzní Fourierovy transformace

(+++) f(x) = ? f°(?) exp(2?i?x)d?

(kde oba integrály vyčíslíme od -? do +?)

Všimněte si, že rovnice (+++) se nápadně podobá formulce (++) a dá se říci, že je její spojitou obdobou. V obou případech se dozvíme, jak se dá signál f(x) složit z frekvenčních komponent. Pro periodické funkce dostaneme součet diskrétní, pro neperiodické součet spojitý (integrál). Za zmínku také stojí to, že ve formulce (+++) frekvenci zcela vyintegrujeme, takže nám zůstane pouze funkce času x (tak jako jsme ve formulce (++) "vysčítali" jednotlivé frekvence reprezentované faktorem n a zůstala nám také pouze funkce času x).

Místo koeficientů cn (které nám ukazují váhu daného n-násobků základní frekvence) tu prostě máme funkci f°(?), která nám ukazuje váhu obecné frekvence ?. A kdybych ten koeficient cn zapsal funkčně jako c(n), tak bude ta analogie ještě patrnější: c(n) je váha frekvence nf, f°(?) je váha frekvence ?.

(c je tedy funkce, která indexům n přiřazuje hodnoty cn)

+++++++++

Počítání Fourierových transformací už je hodně technická záležitost, protože se tam integruje ostošest, někdy i o stosedum. Naštěstí ale existují rozsáhlé tabulky, kde si transformaci své funkce lehce vyhledáte.

Důležité je chápat, co obě funkce znamenají.

f(x) je funkce času a ukazuje prostý záznam signálu
f°(?) je funkce frekvence a ukazuje, jakou váhu má daná frekvence v signálu f(x)

Fourierova transformace nám tedy poskytne frekvenční obraz f° z daného signálu f, zatímco inverzní Fourierova transformace z frekvenčního obrazu f° plně zrekonstruuje původní funkci (signál) f.

Jednou ze zajímavostí Fourierovy transformace je, že Gaussián (tedy jedna z nejdůležitějších matematických funkcí) se převede zpátky na Gaussián, byť s jinými parametry.

Konkretně pro

f(x) = exp(-ax2)

dostaneme

f°(?) = sqrt(?/a) exp(-?2 ?2 / a)

(klidně si to ověřte integrací :-)

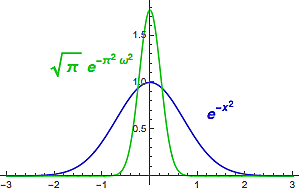
Takže je-li např. f(x)=exp(-x2), zde položíme a=1,  pak f°(?) = sqrt(?) exp(-?2 ?2), což je znázorněno na obrázku vpravo.

Přirozená otázka pak je, zda by se ten Gaussián nedal navolit tak, aby se Fourierovou transformací zobrazoval sám na sebe. A jak asi očekáváte, zařídit to lze a stačí k tomu za a zvolit - hádejte co - no jasně a=?.

Pro exp(-?x2) nám vyjde přesně stejný obraz v časové i frekvenční doméně. Fourierova transformace s touhle funkcí nehne ani o píď. To je fascinující hned ze dvou důvodů. Jednak to ukazuje, že kvadratická exponenciela je invariantní vůči Fourierově transformaci (a připomeňme si, že obyčejná exponenciela je invariantní vůči derivaci), a jednak zde opět vystupuje do popředí tajemná spřízněnost dvou nejdůležitějších matematických konstant e a ?.

(další zajímavosti o Fourierovské invarianci najdete zde)

+++++++++

Zajímavé je na těch Gaussiánech také to, že čím více se snažíte je lokalizovat (tedy zúžit jejich "hrb" v čase), tím více se jejich Fourierova transformace bude rozplizávat (tedy rozšiřovat ve frekvencích). A naopak, když frekvenční spektrum zúžíte, rozplizne se vám časový obraz.

To jsme v extrémní verzi viděli už v první sekci.

Funkce sin(x) má pouze jednu frekvenci, takže její frekvenční obraz je soustředěn v jednom jediném bodě, což je de facto Diracova funkce (ve skutečnosti je to trochu komplikovanější - ale tím si nebudeme kazit příjemný večer).

Funkce sínus, která je v časové doméně rozplizlá prakticky rovnoměrně přes celou reálnou osu, má tedy za Fourierovu transformaci funkci, která je ve frekvenční doméně extrémně koncentrovaná. Sedí pouze v jednom bodě (nebo ve dvou, abych úplně nekecal). Matematikům neuniklo, že lokalizovat funkci v doméně časové i frekvenční je jako zvyšovat současně rychlost i úspornost vaší jízdy autem. Buď pojedete rychle, ale ne úsporně, anebo naopak. Obojí nejde.

A tak začali tento fenomén zkoumat.

Aby tu rozplizlost mohli nějak kvantifikovat, zavedli funkční disperzi D

D(f) = ? x2 f(x)2 dx

která zhruba ukazuje, jak daleko od počátku se funkce "rozvaluje".

Pokud se na výraz f(x)2 budeme dívat jako na pravděpodobnostní hustotu, je to v podstatě formulka pro varianci (s nulovou střední hodnotou). Má-li funkce f(x) výrazné hodnoty daleko od nuly, naintegrujete podstatně víc než pro funkci f, která se šmrdlá pouze v okolí počátku (a jinde je prakticky nulová).

No a ukázalo se, že pro normalizované funkce (jejichž celkový integrál z f(x)2 je 1) platí zajímavá nerovnost:

D(f) D(f°)  ? 1 / 16?2

(s tím, že rovnost nastává právě pouze pro Gaussián!)

Tedy součin disperzí funkce a její Fourierovy transformace musí být větší než určitá konstanta. Nelze je obě udělat libovolně malé. Nelze je tedy lokalizovat současně. Čím je funkce koncentrovanější v časové doméně, tím je její frekvenční obraz rozplizlejší a naopak. A to je Fourierova forma principu neurčitosti.

A jak to souvisí s tím Heisenbergovým?

V jednom starším Matykání jsme viděli, že kvantová mechanika popisuje svět pomocí operátorů a vlnových funkcí. A ta vlnová funkce se dá vyjádřit pomocí poloh a nebo pomocí hybností - stejně jako se naše funkce (signály) daly popsat v časové nebo frekvenční doméně. A ty dva popisy se na sebe dají vzájemně převést Fourierovou transformací. Ta pak v podstatě zabraňuje tomu, aby se vyjádření pomocí polohy a pomocí hybnosti dalo udělat současně libovolně přesné. Takovým dvojicím proměnných - které se brání vzájemné spolupráci - se říká konjugované proměnné.

V tom starším Matykání jsme také viděli, že operátor hybnosti je víceméně operátorem derivace, zatímco operátor polohy je prostým vynásobením funkce jejím argumentem. A Fourierova transformace skutečně převádí derivování na násobení argumentem. Fourierovou transformací derivace, je prosté vynásobení transformace původní funkce jejím argumentem (tj. ?), konkretně:

(f'(x))° = 2?i ? f°(?)

To je ale vykutálený vesmír, co?

Heisenbergův princip neurčitosti je tedy určitým ekvivalentem toho Fourierova.

++++++++++

A takhle se hraje na baskytaru, pacholci. Yes: The Fish (bass: Chris Squire)

Předchozí díly Matykání.