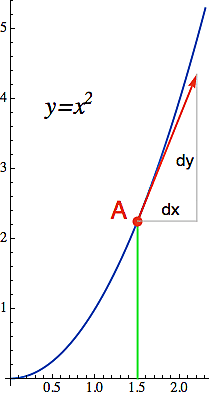Matykání: výlet do infinitesimální džungle

A nebude to žádná procházka růžovým sadem. Jídlo a pití na tři dny s sebou, plus gumáky, deštník, kalkulačku, žákovskou knížku a harpunu. A samozřejmě také potvrzení od rodičů, že pokud vás kousne tygr, můžete si za to sami.

Určitě jste si všimnuli, že Sněžku si prohlédnete daleko lépe pokud stojíte na některém z protilehlých hřebenů než když se nalézáte na úbočí samotné hory. Takový je zákon horské perspektivy. Abyste měli na nějaký vrcholek dobrý výhled, potřebujete určitý odstup.

Infinitesimální počet (zahrnující počet diferenciální a integrální) představuje určitý vrchol základní aplikované matematiky. Dá-li příroda, časem se k němu také prokousáme a na jeho strmých úbočích zažijeme mnohá vzrušující dobrodružství. Protože se ale zrovna nacházíme na protáhlém hřbetu Funkčních hor, máme vzácnou příležitost podívat se na tuto výspu matematického vědění s trochu větším nadhledem než když budeme viset za lano ve skalní stěně Taylorova polynomu a odhánět hladové orly kalkulačkou. Nebudeme se dnes moc babrat v technických detailech, ale spíš se podíváme na klíčové pojmy těchto disciplin přes pomyslný Obří důl.

Předpokládejme, že studujeme nějakou funkci, říkejme jí f(x), a chceme se o jejím chování na daném intervalu dozvědět co nejvíce. K tomuto cíli nám dopomohou další dvě funkce, které jsou z té naší jistým způsobem odvozené: a to je derivace a integrál. Protože víme, že daná funkce není nic jiného než krabička s trpaslíkem, její derivace a integrál nebudou v naší matematické výbavě představovat žádný velký konceptuální skok a pouze do ní přidají dva nové (byť - přiznejme si - trochu jurodivé) trpaslíky. Dokonce uvidíme, že v případě integrálů bude těch trpaslíků nekonečně mnoho. Není proto divu, že Jára Cimrman, sám velký propagátor infinitesimálního počtu v horských oblastech severního Pojizeří, si na jejich pozoruhodnou všudypřítomnost mnohokrát stěžoval, když za svitu petrolejových lampiček vysvětloval chudým tkalcům metodiku navlékání člunku pomocí věty o střední hodnotě.

Pokud s vámi pomocní trpaslíci nebudou chtít během četby spolupracovat, nevěšte hlavu. Stačí vzít harpunu a trochu je tím ostrým koncem popíchnout. A pak spolupracují - a jak!

Ve volné přírodě poznáme derivaci i integrál poměrně snadno a to podle barvy kapitánské pásky na ruce jejich trpaslíka - derivace má červenou a integrál modrou. Fyziognomicky totiž oba pomocní gnómové vypadají přesně jako jejich kolega z původní funkce (tomu jsem pro snadné rozlišení navlékl pásku zelenou). Cimrman to před sto lety svým žákům vysvětloval genderově (to už by asi dneska neprošlo): "říkáme TA derivace, proto má derivace pásku červenou, zatímco TEN integrál má pásku modrou".

Pokud jsme si pro základní funkci vybrali symbol f(x), pro derivaci používáme označení "s čárkou" - tedy f'(x) a pro integrál příslušné velké písmeno - zde F(x). Často se také používá diferenciální značení (na poslední řádce), ale s tím si pro zatím nebudeme dělat starosti (ten prapodivný symbol v pravém dolním rohu, trochu připomínající škvíru v houslích, se vyslovuje integrál).

Nuže, kdo se pročetl až sem, může o sobě směle tvrdit, že již ovládá základy diferenciálního a integrálního počtu. Červená páska derivace, modrá páska integrál. No prosím, jak vám to jde.

Přestože jejich výpočet pro složitější funkce f(x)  dokáže zakabonit čelo nejednoho učence, podstata a praktický význam obou pojmů nejsou ničím, co by běžný středoškolák nemohl pochopit. Kdo se chce o obou pomocných funkcích dozvědět něco více, může pokračovat ve čtení. Zbytek čtenářstva nechť si rozevře záchranný deštník a vyskočí z našeho vzdělávacího balónu.

+++++++++

Mamííí, co je to derivace?

Představ si, že honíš lupiče a policejní vůz Ti právě hlásí, že byli spatřeni na rohu Ječné a Jiráskovy ulice. To samo o sobě Ti ale k úspěšnému pronásledování nestačí. K zachycení jejich stopy ještě potřebuješ zjistit, kterým směrem jeli a jak rychle. Jinými slovy v reálném životě je užitečné vědět nejen kde věci jsou, ale také kam směřují. V matematice k tomuto účelu slouží derivace. Zatímco funkce jako takové popisují stav dané kvantity, derivace nám ukazují, jakým způsobem se tyto kvantity mění - tedy zda rostou nebo klesají a jak rychle. Až ti bude Péťa zase ukazovat, že má stále víc a víc hraček, tak mu prostě řekneš, že počet jeho hraček má kladnou derivaci. Ten bude panečku koukat.

V první řadě si musíme uvědomit, že derivace dané funkce je také jenom funkce (tedy krabička s dalším trpaslíkem, který ze vstupních hodnot vytváří hodnoty výstupní) a není tudíž potřeba se jí bát, natož před ní skákat do kopřiv. Abychom pochopili jak derivace funguje, stačí nám podívat se, co ten červený trpaslík udělá pokud mu do jeho krabičky vhodíme vstupní hodnotu x.

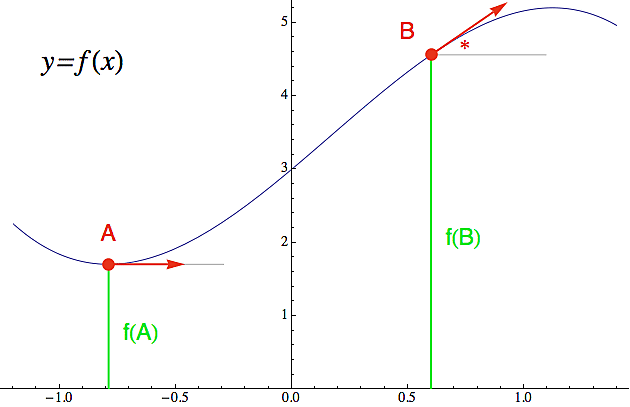
Na následujícím obrázku je libovolná funkce, které budu říkat f(x), a dvě vstupní hodnoty na x-ové ose. Jednu jsem označil A a druhou B. Připoměňme si nejdřív, že pokud do původní funkce (kde žije zelený trpaslík) vhodíte hodnotu A, na výstupu vám trpaslík vyhodí funkční hodnotu y = f(A), a ta vám v podstatě říká, jak vysoko se v tom bodě (x=A) graf funkce nachází. To je ta zelená úsečka. A totéž pro hodnotu B.

My bychom ale chtěli vědět, nejen jak vysoko v daném bodě funkce je, ale také jakou změnu můžeme pro nejbližší hodnoty x očekávat - tedy jakou má funkce v tom bodě tendenci. A to právě zajišťuje derivace. Na obrázku to směřování funkce schematicky vyjadřuje červená šipečka. Teď už jen musíme najít nějaký rozumný způsob, jak tu červenou šipečku proměnit v číslo, které nám bude červený trpaslík servírovat na výstupu derivace.

Nejlepší je se na tu derivaci dívat mechanicky - představte si že ten červený bod je loď, která pluje podél grafu naší funkce (tedy po té modré křice) a ta šipčička je bidlo, které z naší kocábky trčí na přídi (a tím pádem ukazuje kterým směrem momentálně plujeme). Takto definovaný směr plavby můžeme proměnit v číslo tak, že si zaznamenáme úhel mezi tou červenou šipkou a nějakým předem zvoleným směrem - třeba horizontálním směrem vyznačeným světle šedou úsečkou vycházející z daného bodu. U bodu B jsem ten úhel naznačil hvězdičkou (u bodu A je směr plavby totožný se směrem horizontálním, takže ten úhel je tam nula).

Ten úhel sám o sobě ještě není derivace, ale už jsme blízko. A pomůžeme si jednou vychytávkou ze středoškolské matematiky.

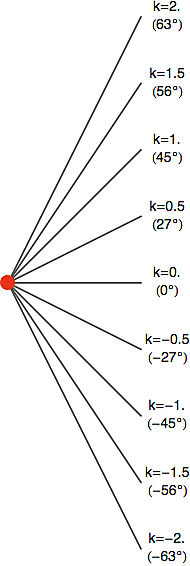
Z pohledu analytické geometrie je přímka lineární funkcí s rovnicí y = kx+q, kde q je průsečík přímky s osou ypsilon a k je tzv. směrnice přímky, tedy tangens jejího úhlu. Na obrázku vpravo vidíte několik přímek vycházejících z červeného bodu, včetně jejich směrnic (a odpovídajících úhlů). Máte-li po ruce kalkulačku, můžete si sami ověřit, že ta směrnice je skutečně tangens naznačeného úhlu.

Vidíte, že pokud přímka ani neklesá, ani nestoupá, její směrnice je 0. Klesající přímky mají zápornou směrnici k (a čím rychleji klesají, tím zápornější ta směrnice je), zatímco stoupající přímky mají směrnici kladnou.

A teď můžeme v definici derivace udělat poslední krok. Ten červený trpaslík nám na výstupu prostě vyhodí směrnici přímky určené tou červenou šipečkou (jmenuje se Slečna Tečna, ale seznámit se s ní nepokoušejte - je poměrně netečná). Jinými slovy, derivace v daném bodě není nic jiného než směrnice tečny ke grafu funkce v tom bodě.

Ta derivace (coby funkce) tedy funguje takto. Vhodíte do trpaslíkovy krabičky nějakou vstupní hodnotu x, trpaslík si vyhledá bod na grafu původní funkce, který odpovídá příslušné souřadnici x a v tom bodě si nakreslí červenou šipečku. Pak se podívá jaký úhel ta šipečka svírá s kladným směrem podél osy x (horizontální směr) a na výstup vám vyhodí tangens toho úhlu.

Protože tangens převádí kladné úhly na kladná čísla a záporné na záporná, derivace nám velmi intuitivně ukazuje zda funkce v daném bodě roste a nebo klesá. Pokud funkce roste (šipečka trčí vzhůru), úhel mezi šipečkou a šedou referenční úsečkou bude kladný a tudíž derivace (coby směrnice neboli tangens tohoto úhlu) bude taktéž kladná. Pokud funkce klesá, úhel bude záporný a i derivace bude záporná. A čím strměji funkce klesá, tím zápornější bude její derivace.

Podívejme se na obrázek vlevo. Protože tangens je protilehlá ku přilehlé, derivace dané funkce v bodě A není nic jiného než poměr přírůstku y-ové složky (který jsem označil jako dy) k přírůstku x-ové složky (dx) podél té tečny. To písmenko d pochází z řeckého delta, kterým se obvykle vyznačuje změna v hodnotě nějaké proměnné. Máme tedy:

f'(A) = dy/dx  (*)

To nám umožňuje velmi vizuální interpretaci čísla, které nám červený trpaslík (derivace) vyhazuje na výstupu.

Ta funkce vlevo je f(x)=x2 a v tabulkách si najdeme, že její derivací je funkce f'(x) = 2x (druhý řádek shora, kde položíme n=2). Pokud tedy chceme vědět, jak rychle ta kvadratická funkce stoupá v naznačeném bodě x=1.5, prostě toto číslo předhodíme červenému trpaslíkovi a ten nám na výstup pošle hodnotu f'(1.5) = 2*1.5 = 3. Takže derivace v bodě x=1.5 je 3.

Z formulky (*) nyní dovodíme, že v bodě A platí

3 = dy/dx neboli dy = 3*dx

Když si vezmete silnou lupu a podíváte se na okolí toho červeného bodu, uvidíte, že lokálně se ta funkce chová jako přímka se směrnicí 3. To znamená, že na každý krok doprava, udělá tři kroky směrem vzhůru (derivace svazuje nárůst závisle a nezávisle proměnné).

Kdo má rád fyziku, může se na to dívat přes rychlost.

Představme si, že v čase 0 vyšleme z bodu A autíčko, které v čase t dojede do bodu B.

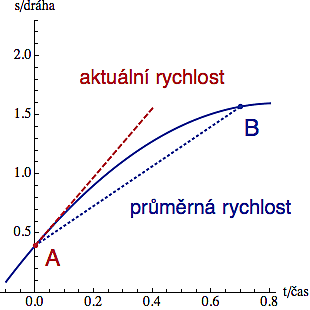
Průměrnou rychlost mezi naznačenými kontrolními body (vpravo) spočítáme tak, že přírůstek dráhy vydělíme přírůstkem času. Z matematického pohledu de facto počítáme směrnici té modré sečny.

Často ale potřebujeme znát aktuální rychlost (tedy tu na tachometru) a tu získáme tak, že kontrolní bod B přiblížíme "infinitesimálně blízko" k bodu A. V něm se modrá sečna promění v červenou tečnu a její směrnice nám prozradí aktuální rychlost v bodu A (a protože směrnice tečny není nic jiného než derivace, říkáme, že rychlost je derivace dráhy podle času).

Derivace funkce v daném bodě tedy ukazuje aktuální rychlost změny naší funkce, tj.aktuální (okamžitý) nárůst závisle proměnné (y) v poměru k nárůstu nezávisle proměnné (x). Je to vlastnost čistě lokální a závisí pouze na chování funkce v nejbližším okolí daného bodu.

Získat tuto informaci prostřednictvím jednoho čísla je mnohem praktičtější než zelenému trpaslíkovi zkusmo do krabičky naházet hafo hodnot kolem x a při tom pozorně sledovat, co se děje na výstupu.

++++++++++

Tatííí, co je to integrál?

Představ si, že jdeš po silnici a na každém patníku leží mince. Jako každý chudý školák minci sebereš a dáš si ji do tobolky. To, co je pro tebe důležité ale není to, jaká mince na tom kterém patníku právě leží - třeba je to jen koruna - ale jakou celkovou hodnotu mají mince v tvé tobolce. Na těch ostatních patnících mohly klidně ležet třeba dvacky. V praktickém životě nás vždycky zajímá hlavně nastřádaná (kumulativní) hodnota, ne momentální kořist. No a mezi funkcemi hraje roli kumulativního indikátoru právě integrál, který do jisté míry ukazuje, kolik kvantity reprezentované danou funkcí sis zatím nahamounil. Tady například uvažujeme funkci, která každému patníku přiřazuje určitou minci. Tak až se Péťa bude zase vytahovat, že nasbíral cennější mincí než ostatní, tak mu prostě vysvětlíš, že jeho silnice má větší integrál. A ono mu sklapne.

Stejně jako derivace, integrál není nic jiného než prachobyčejná funkce (trpaslík s modrou kapitánskou páskou), takže se podívejme co tento pidimužík udělá, pokud mu do krabičky vhodíme nějakou vstupní hodnotu x.

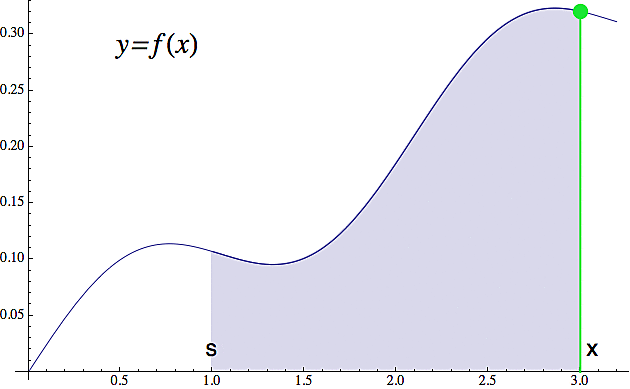
Každý modrý trpaslík má ve své skříňce zapsanou určitou startovní hodnotu s (ta se může trpaslík od trpaslíka lišit) a když mu do krabičky vhodíte číslo x, tak si ten trpaslík změří plochu pod grafem původní funkce f(x) od té startovní hodnoty s až po vaše zadané číslo x. No a velikost této plochy vám potom vyhodí na výstupu (na obrázku je vystínovaná modře). Nic víc a nic míň.  Musí se tam sice dávat trochu bacha na znaménko - tedy zda je funkce kladná (nad osou x) a nebo záporná (pod osou), ale s tím si zatím nebudeme lámat hlavu.

Funkce, která takto funguje se jmenuje integrál té původní funkce f a obvykle se značí příslušným velkým písmenem - v našem případě tedy F(x) a nebo integrálním symbolem F = ?f (v plné verzi: F(x) = ?f(x)dx). Někdy také té funkci F(x) říkáme primitivní funkce a angličtina pro ni má dokonce výraz anti-derivace, který naznačuje, že v jistém smyslu je integrál protějškem derivace (koho to zajímá podrobněji, vysvětlení najdete na konci sekce Jauvajs).

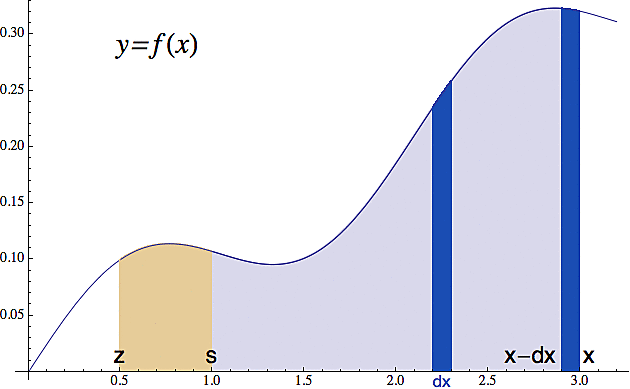
V praxi nás většinou zajímá velikost té plochy pod funkcí mezi nějakými dvěma konkretními hodnotami (tedy lidově vocuď-pocuď), s tím, že to vocuď nemusí být nutně ta startovací hodnota s, kterou má každý trpaslík zafixovanou (pravděpodobně ve stropě). Proto se při počítání ploch pod funkcemi v našich výpočtech většinou objevuje rozdíl hodnot primitivní funkce v těch dvou bodech (vocuď pocuď). Jako příklad (viz další obrázek) si odvodíme výraz pro plochu té poslední tmavomodré "nudličky" mezi hodnotami x-dx a x (zde je dx libovolné číslo naznačující šířku té nudličky). Když se na to budeme dívat čistě geometricky, tak nám stačí obě hodnoty předhodit modrému trpaslíkovi (integrál) a odečíst, tedy spočítat F(x) - F(x-dx). Rozmyslete si, že toto vám skutečně dá kýženou plochu (ten první člen vyjadřuje plochu od s do x, ten druhý od s do x-dx a jejich rozdíl je přesně to, co potřebujete).

Aby nám ta startovací hodnota s nevrtala v hlavě moc dlouho (s děravou hlavou se špatně počítá), podíváme se jí trochu na zoubek.

Protože žijeme v době volného trhu, může se stát, že pro výpočet integrálu dané funkce f nabídnou své služby dva nezávislí trpaslíci. Ten původní, říkejme mu Standa, který na výstupu vyhazuje velikost plochy pod funkcí od hodnoty s (kterou si vybral, když skládal trpaslické zkoušky) do hodnoty x (kterou jste mu vhodili na vstupu vy) a potom jeho konkurent, kterému budeme říkat Zdenda, a ten velikost té plochy počítá od z (jako "začátek") do x (viz obrázek nahoře).

Z geometrie je jasné, že když oběma hodíte na vstup to samé číslo x, jejich výstupní hodnoty se budou lišit přesně o velikost té světle hnědé plochy, říkejme jí C. To znamená, že pokud je Zdenda mazanej, tak po vašem vhození x nejprve zavolá Standovi, zeptá se jak velkou plochu pro to konkretní x dostal a pak k ní prostě přičte C a hodí vám to na výstup. Jinými slovy, obě primitivní funkce, Standova i Zdendova, se liší pouze o tu konstantu C. A protože máme nekonečně mnoho možností pro výběr toho počátečního bodu, máme de facto pro každou funkci f(x) nekonečně mnoho primitivních funkcí, ale všechny se liší pouze o konstantu. To se při výpočtu obvykle zohlední tak, že k té primitivní funkci automaticky připlácneme libovolnou konstantu:  F(x)+C (říká se jí "integrační konstanta").

Protože nás z výše uvedených důvodů většinou zajímá rozdíl hodnot primitivních funkcí, nemusíme si s tou konstantou dělat hlavu. Ona se při výpočtu vyruší. Např. ta tmavomodrá nudlička vpravo na předchozím obrázku bude mít podle jiného trpaslíka plochu (F(x)+C) - (F(x-dx)+C), což vede opět k výrazu F(x) - F(x-dx).

Tu neurčitost v definici integrálu si můžeme představit jako počítání let v kalendáři. Západní civilizace si jako startovní bod vybrala (nejpravděpodobnější) rok narození Krista, ale pokud bychom si vybrali třeba rok narození Karla IV, dostali bychom obdobný kalendář, který by začínal v roce 1316 a na ten křesťanský se dal lehce přepočítat. Sám Karel by podle takového kalendáře žil v letech 0 až 62 (po Karlovi), zatímco podle standardního kalendáře žil v letech 1316 až 1378 (po Kristovi). V obou případech se dožil 62 let. Ten rozdíl musí být stejný. A z podobného důvodu dostaneme stejnou plochu pod funkcí (počítáno vocaď pocaď) - ať už ji zadáme Standovi (který začíná měřit v bodě s) a nebo Zdendovi (který začíná v z). Rozdíl primitivních funkcí musí být stejný.

+++++++++

Tak - teď když jsme se probrodili konstantami a ta náhodně vybraná startovací pozice už nás netrápí, podíváme se, co Standa v té své krabičce vlastně dělá, když pro nás tu plochu počítá. Pokud se dá primitivní funkce F(x) vyjádřit vzorečkem, tak do něj Standa prostě dosadí x a pošle vám výsledek na výstup. Existují ovšem poměrně jednoduché funkce, např. sin(x)/x, pro které ani v 21. století tu primitivní funkci stále neznáme, respektive ji neumíme vyjádřit pomocí známých funkcí. V takovém případě se Standa musí uchýlit k malé lsti, které se říká numerická integrace.

Představme si, že máme spočítat tu světle modrou plochu od nějaké hodnoty a (vocaď) do nějaké hodnoty b (pocaď). Na obrázku výše je a=1 a b=3.

Nejprve si tu světle modrou plochu rozřežeme na N tmavomodrých nudliček, takže každá z nich bude mít šířku dx = (b-a)/N. Tedy slovy: délka intervalu dělená počtem nudliček. Na obrázku jsou ty nudličky jen dvě - aby nebyl moc přeplácán - ale pokud si je představíte všechny, uvidíte jako na dlani tu kumulativní vlastnost integrálu. Každá ta nudlička představuje "mincovní úlovek" naší funkce f(x) na nějakém úzkém intervalu, na kterém je ta funkce zhruba konstantní. A při počítání celé plochy ty malé plošky de facto sčítáme (integrál taky není nic jiného než určitá forma nekonečného a dokonce nespočetného součtu).

Protože křivočaré plochy moc počítat neumíme, budeme se tvářit, že každá ta nudlička je plus-mínus obdélník (za tím účelem ji nahoře lehce opilujeme) a žádanou plochu získáme sečtením ploch všech obdélníkových nudliček (bude tam sice trochu chybka, ale jako první aproximace nám to stačí). Šířka každé nudličky je dx a její výška je určená funkční hodnotou v nějakém bodě dané nudličky.  Ty hodnoty si označíme jako f1, f2, ..., fN a spočítat je není žádný problém. Hodnotu x, kterou jsme si z každé nudličky vybrali, předhodíme zelenému trpaslíkovi (ten co šéfuje té původní funkci f) a máme vystaráno. Který konkretní bod jsme si z každé nudličky vybrali je víceméně jedno. Pokud jsou ty nudličky dostatečně úzké (tj. N je dostatečně veliké), tak je ta funkční hodnota uvnitř každé nudličky prakticky konstantní. Takže pro výslednou plochu dostaneme přibližně tento součet nudličkových ploch:

P = (f1 + f2 + f3 + ... fN)*dx = (b-a) * (f1 + f2 + f3 + ... fN) / N

A to je číslo, které nám Standa vyhodí na výstupu. Současně jsme si ale připravili půdu pro jednu zajímavou aplikaci integrálu.

Když se podíváte na ten předchozí vzoreček, tak na jeho pravé straně vpodstatě vidíte průměrnou funkční hodnotu mezi body x=a a x=b. Pokud si ji označíme PFH, dostaneme pro ni výraz PFH = P/(b-a). A protože ve fyzice je výpočet průměrných hodnot funkce na nějakém intervalu (a,b) jako houska na krámě, máme zde univerzální návod: stačí spočítat plochu P (integrálem), pak vydělit délkou intervalu a průměr je na světě.

A taky obráceně. Plochu můžeme vydundat z průměru. Představte si třeba, že ta funkce f(x) z předchozího obrázku je teplotní křivka, která vylézá z nějakého měřicího přístroje. Tady samozřejmě nemáme šanci vyjádřit primitivní funkci vzorečkem, protože neznáme ani vzoreček pro funkci původní. Tu numerickou integraci si teď můžete vyložit tak, že změříte teplotu každou minutu (nebo nějaký jiný malý interval), tím dostanete posloupnost f1, f2, ..., fN, pak prostě spočítáte její aritmetický průměr a nakonec ho vynásobíte faktorem (b-a). A plocha je na světě.

Integrál funkce přes nějakou množinu (zde interval [a,b]) je v podstatě průměr té funkce na dané množině krát velikost té množiny (zde délka intervalu [a,b]).

Na závěr si ukážeme jeden příklad, kdy se ten integrál dá vyjádřit formulkou, takže příslušnou plochu získáme jako rozdíl hodnot primitivní funkce. Vezměme si opět třeba kvadratickou parabolu mezi body 1 a 3 (obrázek vpravo). Protože integrovat zatím neumíme, vyhledáme si primitivní funkci v tabulce integrálů (je to první řádek, kde položíme n=2). Ta tabulka nám vlastně ukazuje, jak ze zelených trpaslíků (první sloupec) vytvořit ty modré (druhý sloupec).

V našem případě je primitivní funkcí F(x) = x3/3, takže dosadíme obě hodnoty a odečteme: naznačená plocha od 1 do 3 má tedy velikost

P = F(3) - F(1) = (33 - 13)/3 = 26/3 = 8.6666...

Pro průměrnou funkční hodnotu mezi body 1 a 3 pak vychází

PFH = P/(b-a) = 8.666... / 2 = 4.333...

Všimněte si, že ta průměrná hodnota je o něco méně než 5, což je průměr z funkčních hodnot v koncových bodech (12=1 a 32=9). To je proto, že funkce na tom intervalu trochu "zatahuje bříško" (takovým funkcím říkáme "konvexní").

Rychlé shrnutí dnešního výletu:

Pro danou funkci f nám funkční hodnota f(x) v bodě x ukazuje jak vysoko je graf funkce nad osou x. Derivace této funkce f'(x) v bodě x nám ukazuje směrnici tečné přímky (to je přímka ve směru té červené šipky) a tedy vypovídá o tom, jak rychle funkce v tom bodě roste nebo klesá. A konečně primitivní funkce (neboli integrál) F(x) v bodě x nám udává plochu pod funkcí f(x) od nějakého referenčního bodu do bodu x. A to nám prozatím bude stačit.

+++++++++

Sekce jauvajs: A jak se tedy ty vymyšlenosti vlastně počítají?

jen pro mimořádně otrlé jedince

Podíváme se nejprve v kostce, jak se počítá derivace. Tedy jak ze zeleného trpaslíka udělat červeného. Přesněji jak ze vzorečku pro funkci vyždímat vzoreček pro její derivaci. Protože diferenciální počet je téma na několik vysokoškolských přednášek, ukážu vám jenom malý příklad.

Při tomto výpočtu se počítá s nekonečně malými (tzv. infinitesimálními) veličinami. Prozatím si je můžete představovat jako velmi malá desetinná čísla (např. 0.000001). Připomenu vám ale jednu důležitou vlastnost malých čísel. Jejich čtverec (druhá mocnina) se dá z praktického hlediska zanedbat. Např. 0.012 je 0.0001, zatímco 0.0012 už je 0.000001. A čím je to číslo menší, tím je snadnější jeho čtverec zanedbat (i když malinká chybka tam pořád bude). Důvod, proč si matematici vymysleli infinitesimální veličiny je, že teprve pro číslo nekonečně malé se ten čtverec dá zanedbat "přesně".

Tak a teď do díla.

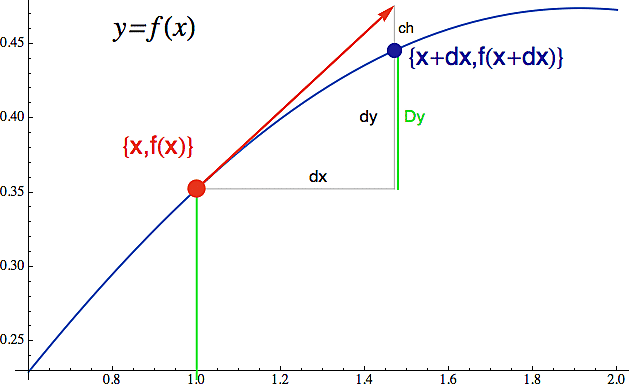
Na následujícím obrázku máme bod na grafu funkce f(x) (jeho souřadnice vidíte v kroucené závorce) a zajímá nás, jak spočítat směrnici tečny dané tou červenou šipčičkou. Protože směrnice je tangens úhlu přímky, ptáme se jak spočítat podíl dy/dx (protilehlá ku přilehlé), pro nějakou rozumnou hodnotu dx (tu si můžeme zvolit celkem libovolně, protože délka té červené šipky je na nás). Problém je jak pro to zvolené dx spočítat dy (a zdůraznil bych, že to dy je nárůst y podél tečny, takže nahoře sahá až po okraj té červené šipečky!).

Když o tom budete chvíli přemýšlet, zjistíte, že daleko jednodušší by bylo místo dy spočítat naznačené Dy, které sahá pouze po ten modrý bod. Jeho souřadnice lze v pohodě získat dosazením do původní funkce (najdete je opět v závorce) a toto Dy by se pak dalo spočítat jako rozdíl y-ových souřadnic obou bodů. Tímto postupem (nahrazením přírůstku dy podél tečny přírůstkem Dy podél funkce) se však dopustíme určité chyby, kterou jsem na obrázku vyznačil písmenkem "ch".

Celá krása infinitesimálního počtu spočívá v tom, že pokud to dx bude velmi malé, tak se chyba ch stane zanedbatelnou a bude v podstatě jedno, zda do vzorečku pro směrnici přímky dosadíme dy nebo Dy. To je vidět tak, že s tím modrým bodíkem budete ve své mysli couvat zpátky k bodu červenému a při tom pozorovat, jak se ta chyba ch postupně zmenšuje. No a pokud by to dx bylo "nekonečně malé", tak by ta chybka ch byla vlastně zcela nepodstatná. Sečna procházející červeným a modrým bodem by pak splynula s tečnou a její směrnice Dy/dx by se stala směrnicí tečny.

Takže si to "funkční" Dy rozepíšeme (pro dx "velmi malé") jako rozdíl

Dy = f(x+dx) - f(x)

a dosadíme ho drze do směrnice tečny namísto "správného" dy:

f'(x) = dy / dx = Dy / dx = ( f(x+dx) - f(x) ) / dx

(kde ta druhá "rovnost" se v reálu musí ošetřit limitou)

Pomocí tohoto vzorečku si zkusíme spočítat třeba derivaci funkce f(x) = x2

f'(x) = ((x+dx)2 - x2)/dx = (2x*dx + dx2)/dx = 2x*dx / dx = 2x

(tady jsme roznásobili a použili fakt, že pro malé dx se dx2 dá zanedbat!)

Dostali jsme přesně ten samý výsledek, který jsme si v sekci o derivacích museli vyhledat v tabulce. Takhle se ty derivace v zásadě počítají - jenom se dnes používá limitní zápis, protože manipulace s nekonečně malými veličinami trochu plave na vodě (i když je velmi intuitivní).

A co s integrály?

No, to už je vysloveně džungle. Výpočet integrálů je v mnoha případech komplikovanější než sestavení vrtné plošiny ze stavebnice IKEA. Ale jednu věc vám přece jen ještě ukážu.

Zkusme si spočítat derivaci integrálu. Tedy co by se stalo, kdybychom čapli toho trpaslíka s modrou páskou a na ruku mu ještě narvali pásku červenou.

Pro derivaci primitivní funkce použijeme stejný trik jako nahoře:

F'(x) = ( F(x+dx) - F(x) ) / dx

když si rozmyslíte, co máme v té závorce - je to vlastně rozdíl dvou ploch a to co tam po odečtení zbyde je de facto plocha té závěrečné modré nudličky (z obrázku u integrálů), kterou můžeme opět odhadnout jako obdélníček o malé šířce dx a výšce odpovídající náhodně zvolené funkční hodnotě z podstavy toho obdélníčku. Protože se ale nacházíme mezi x a x+dx (kde dx je velmi malé), můžeme si za to náhodně zvolené číslo vybrat přímo x, takže výška té "nudličky" pak bude přímo f(x). Opět velkoryse zanedbáme to, že ten obdélníček je nahoře trochu pokřivený a dostaneme:

F'(x) = (plocha té poslední nudličky) / dx = (f(x) * dx) / dx = f(x)

Zjistili jsme tedy, že derivace toho tajemného integrálu je původní funkce (tedy většinou - občas to z různých důvodů nefunguje). A tento nenápadný postřeh nám umožní spoustu integrálů spočítat přesně - tedy najít vzoreček pro primitivní funkci.

Nahoře jsme například spočítali, že derivací funkce x2 je funkce 2x.

Co by asi tak mohlo být integrálem funkce 2x? A nezapomeňte, že derivací integrálu je původní funkce. Takže ať to bude co to bude, musí to mít derivaci 2x. Neznáme náhodou nějakou funkci, jejíž derivací je 2x? Ale to se ví, že známe. To je přece x2. A vida, právě jsme spočítali svoji první primitivní funkci. Integrálem funkce 2x je x2. A ani to nebolelo.

Integrování a derivování jsou tedy v jistém smyslu inverzní operace. Jako když jedete do Pyšel a pak zase z Pyšel.

+++++++++

Na oddech si dnes dáme jednu zajímavou komposici z dílny zpěváka Jona Andersona a řeckého keyboardisty, který si říká Vangelis. Jmenuje se "State of Independence" a Jon Anderson ji natočil před několika lety s islandským souborem Todmobile. Nevím proč, ale nějak mi k tomu infinitesimálnímu počtu pasuje. Původní verzi z 80. let i s textem naleznete zde.

Předchozí díly Matykání.