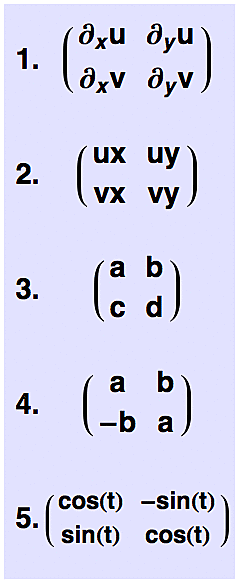Matykání: pane íčko, na slovíčko
Z pohledu fyzika nebo inženýra nemají komplexní funkce příliš prostoru k praktickému uplatnění. Většina procesů, které pozorujeme kolem nás se dá zcela uspokojivě popsat reálnými funkcemi, takže stačí dobře se naučit infinitesimální počet (v reálných proměnných) a je vystaráno.
Z pohledu matematika však rozšíření běžných reálných funkcí do komplexního oboru představuje vítanou příležitost pozorovat jejich chování v daleko širším kontextu. O tygrovi se toho moc nedozvíte, pokud ho budete pozorovat jenom při jeho přecházení sem a tam v cirkusové kleci. Jakmile ho ale vypustíte do džungle, dozvíte se o něm věci, které vás možná budou až mrzet.
O funkcích platí v jistém smyslu totéž co o číslech: pokud se při jejich studiu omezíte jen na reálnou osu, sledujete pouhou siluetu tanečního vystoupení promítnutou na stěnu sálu. Pokud je chcete matematický uchopit v plné barvitosti, musíte se volky nevolky vydat do komplexní roviny a pohlédnout tváří v tvář jejich skutečnému obrazu.
+++++++++
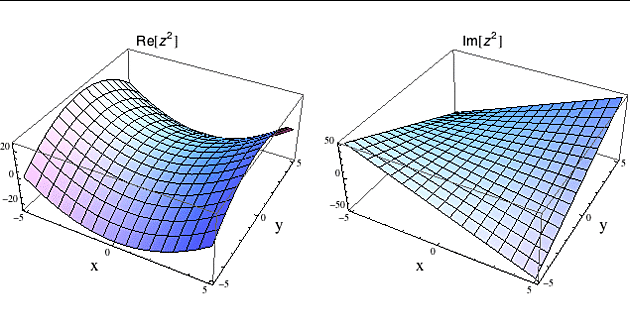
Minule jsem vám ukázal, že když rozdělíme komplexní funkci na její reálnou a imaginární složku, získáme de facto dvě funkce v reálných proměnných x,y. Na obrázku je to ukázáno pro funkci f(z)=z2, která se po takovém rozdělení rozpadne na dvě reálné funkce u(x,y)=x2-y2 a v(x,y)=2xy.
(stačí si rozepsat z=x+iy a provést naznačené umocnění)
Když takové dvě funkce "slepíme" dohromady, dostaneme reálný ekvivalent komplexní funkce, tedy funkci F z R2 do R2 (má dva reálné vstupy a dva reálné výstupy), která funguje takto:
F: {x,y} --> {x2-y2,2xy}
(Na té pravé straně bychom pochopitelně mohli zkusit i jiné mocniny proměnných x,y třeba s nějakými náhodně zvolenými koeficienty a pořád bychom dostali reálnou funkci z roviny do roviny - ovšem zdaleka ne každá taková nahodilá změť x a y se dá přetavit komplexní funkci. V sekci Jauvajs se zmíním, za jakých okolností by se z takové reálné spatlaniny dala vytvořit komplexní funkce)
Když studenti technických oborů tu reálnou verzi komplexní funkce vidí, nasadí většinou znuděné výrazy a začnou nespokojeně reptat: "ale takovéhle funkce my přece známe - ty umíme derivovat už z diferenciálního počtu více proměnných a všechny jejich vlastnosti máme v malíčku... nemohli bychom jít raději do hospody?".
No, nemohli.
V dnešním článku se pokusím vám ukázat, že komplexní funkce mají spoustu vlastností, o kterých se reálným funkcím ani nesní. A může za to pan Íčko. Zatímco z pohledu reálných funkcí se rovina skládá z dvou nezávislých kopií číselné osy a na její bodíky se díváme jako na vektory, v komplexní analýze jsou obě osy propojeny algebraickou vazbou komplexních čísel a na bodíky pohlížíme jako na skaláry. A ty představují daleko kompaktnější a ucelenější strukturu. Aby komplexní funkce na té struktuře mohli nějak slušně vyžít, například mít derivaci, jejich chování musí být podstatně uspořádanější než chování jejich reálných protějšků.
(celá příští sekce je poměrně technická a pokud chcete získat jen jakous takous představu o čem je dnes řeč, můžete ji přeskočit)
++++++++++
Komplexní derivace
Nejprve malá rekapitulace reálné derivace (a zpřesnění již řečeného).
Na grafu dané (prozatím reálné) funkce si označíme jeden pevně zvolený bod A = {x0,y0} a začneme zkoumat chování funkce v jeho okolí. Za tím účelem hodnotu nezávisle proměnné trochu "šoupneme" (do obecného bodu x) a zjistíme, že hodnota závisle proměnné se po tomto zásahu posunula do bodu y.
To, co nás zajímá, je vztah mezi x-ovým přírůstkem dx (zeleně) a y-ovým přírůstkem Dy (fialově) v okolí daného bodu.
Bohužel pro většinu funkcí je takový vztah stejně komplikovaný jako funkce sama - abychom nárůst Dy spočítali, museli bychom znovu vyčíslit naši funkci.
Naštěstí si ale nějací koumesové v minulosti povšimli (a na tom v podstatě stojí diferenciální počet), že pokud se omezíme na malé změny dx, můžeme tu funkční křivku (v modrém) nahradit tečnou (v červeném) a spočítat její nárůst dy, což je podstatně jednodušší úloha.
Mezi dx a dy existuje lineární vztah a to znamená, že tyto dva přírůstky jsou v okolí zvoleného bodu x0 proporcionální, přičemž konstantou úměrnosti je právě hodnota derivace f'(x). Je-li její hodnota v našem bodě rovna řekněme f'(x0)=2, z pohledu inženýra to znamená, že každý rozumně malý nárůst dx vstupní hodnoty vyvolá na výstupu proporcionální nárůst o velikosti dy=2*dx. Tato hodnota je velmi dobrou aproximací Dy (pro odhad výstupního přírůstku už nemusíme vyčíslovat funkci). Prostě jenom každé dx pronásobíme derivací a hned víme jaké bude dy (tj. o kolik se zhruba posune y).
Čím je dx menší, tím je tento odhad přesnější - proto se této habaďůře říká infinitesimální počet (týká se veličin, které si představujeme jako "nekonečně malé"). Pro nelineární funkce se červená tečna začne dříve nebo později odchylovat, takže ta aproximace platí jen v okolí bodu A. Jakmile s ním trochu pohnete, derivace se změní (protože do vzorečku dosadíte jinou hodnotu x) a převodový poměr dy/dx v jeho okolí se změní také. Pouze přímky – tedy lineární funkce – mají derivaci konstantní, protože rostou či klesají stále stejným tempem.
Takto si vytvoříme naši první aproximaci lokálního chování funkce. Zafixujeme si bod x0 a ten druhý bod x necháme volně pobíhat po jeho okolí:
f(x) = y ~ y* = f(x0) + dy = f(x0) + f'(x0) * dx = f(x0) + f'(x0) * (x-x0)
Na levé straně je funkce, na pravé tečna. A "vlnovka" ~ zde znamená přibližnou rovnost (to y* jsme totiž dostali pomocí tečného přírůstku a nikoliv funkčního - je tam tedy malá chybka - rozdíl mezi tou červenou a fialovou šipkou).
Mimochodem, podobným způsobem se funkce rozvine v mocninnou řadu. Napravo se prostě přidávají další členy s vyššími derivacemi a ty postupně tu "vlnovku" zpřesňují a zpřesňují až výsledně dostaneme rovnost (pro nekonečně mnoho členů napravo). Takhle ta formulka bude vypadat, přidáme-li druhou derivaci f'' (tedy derivaci první derivace):
f(x) ~ f(x0) + f'(x0) * (x-x0) + f''(x0) * (x-x0)2 / 2 + ...
Rozvoj v takovouto mocninnou řadu si můžete udělat kolem libovolného bodu x0. V praxi se ale většinou používají rozvoje kolem bodu 0, čemuž jsem v minulosti říkal nekonečné polynomy (přesněji Maclaurinovy řady). Ovšem už přidání toho kvadratického členu napravo není nic jednoduchého, takže hlouběji se v tom zatím šťourat nebudu.
+++++++++
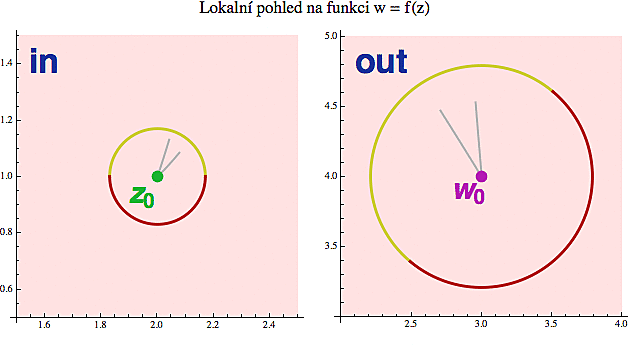
Na komplexní derivaci se můžeme také dívat optikou "přírůstků" (viz obrázek níže). Jen budeme proměnným v souladu s konvencí říkat z a w místo x a y. Hodnotu f'(z0) si tedy představíme jako (komplexní) číslo, které má tu vlastnost, že když s ním pronásobíme přírůstek nezávisle proměnné z, dostaneme nejpřesnější aproximaci přírůstku závisle proměnné w.
Opět si zafixujeme nějakou pevnou vstupní hodnotu z0 a trochu ji "šoupneme" o hodnotu dz, čímž se dostaneme do bodu z. Zajímá nás, jak se takové "šoupnutí" projeví na výstupu w0=f(z0). A máme opět dvě možnosti. Buď si to spočítáme přesně pomocí funkční hodnoty, tj. zobrazíme ten "šoupnutý" bod z přímo do bodu w = f(z) a odečtením získáme hodnotu přírůstku Dw = w-w0 a nebo použijeme derivaci v bodě z0 a posuneme výstup w0 pouze o hodnotu dw = f'(z0)*dz. Tak se dostaneme do "přibližného" bodu w* = w0+dw = f(z0) + f'(z0)*dz. Pokud máte derivaci spočítanou správně a to šoupnutí dz není moc velké, měli byste s bodem w* přistát někde poblíž w.
Všimněte si, že k výpočtu toho přibližného bodu w* vůbec nepotřebujete funkční hodnotu (pouze vynásobíte přírůstek dz komplexní derivací a přičtete k w0), takže můžete poměrně rychle získat představu o lokálním chování funkce f(z) v okolí bodu z0 jenom ze znalosti čísla f'(z0).
Formálně má většina komplexních funkcí stejnou derivaci jako odpovídající funkce reálné, takže s výpočtem není problém - například funkce f(z)=z2 má derivaci f'(z)=2z.
+++++++++
Aby do toho obrázku bylo lépe vidět, udělejme si malý příklad, jak ty komplexní přírůstky vlastně fungují.
Vezmeme si již zmíněnou funkci f(z)=z2 a budeme zkoumat její chování v okolí komplexního čísla z0 = 2+i. Přímým dosazením zjistíme, že naše funkce ho zobrazí do bodu w0 = f(z0) = f(2+i) = 3+4i. A teď si vezmeme malý přírůstek dz = -0.3+0.2i, které nás dopraví do bodu z = z0+dz = 1.7+1.2i . Na výstupu se náš bod w0 přesune do odpovídajícího bodu w = f(z) = f(1.7+1.2i) = 1.45+4.08i . No a odečtením dostaneme výsledný nárůst proměnné w jako Dw = w-w0 = -1.55+0.08i .
My ale nechceme pro každý přírůstek dz pracně vyčíslovat funkční hodnotu v tom "šoupnutém" bodě z. My chceme ten odpovídající nárůst proměnné w dostat hned z toho dz pomocí derivace (byť jen přibližně). Tu stačí vyčíslit jen jednou a příslušné komplexní číslo f'(z0) pak funguje pro libovolný přírůstek dz.
dw = f'(z0) * dz
Nuže derivace f'(z) = 2z a dosazením z0 dostaneme f'(z0)=2(2+i) = 4+2i. Takže pro přírůstek dw "podél tečny" nám vyjde
dw = (4+2i)*(-0.3+0.2i) = -1.6 + 0.2i
a to není moc daleko od výše uvedené přesné hodnoty Dw.
A když to posunutí dw přidáme k hodnotě w0, získáme poměrně solidní aproximaci bodu w aniž bychom museli znovu vyčislovat funkci f(z).
w ~ w* = w0 + dw = 3+4i + (-1.6 + 0.2i) = 1.4 + 4.2i
Takže shrnuto a podtrženo - komplexní derivace je číslo, které nám - stejně jako v reálném případě - udává poměr mezi změnou vstupní hodnoty dz a výstupní hodnoty dw. Pokud se takové číslo dá najít v každém bodě z0, říkáme, že naše komplexní funkce je holomorfní (a žádné jiné v tomto článku ani uvažovat nebudu).
+++++++++
Komplexní derivace má pro pochopení chování funkce v okolí bodu z0 klíčový význam. V jednom čísle je zakódováno chování milionů funkčních hodnot z nejbližšího okolí bodu z0 (!).
Abychom do věci lépe viděli, napišme si ji v polárních souřadnicích f'(z0)=r*exp(it):
dw = f'(z0)*dz = r*exp(it)*dz
Když to budu číst zprava, tak ta rovnice mi říká, že abych dostal přibližný přírůstek dw, tak musím vzít přírůstek dz a vynásobit ho nejprve komplexním číslem exp(it) a potom reálným číslem r. Připomeňme si, co s ním tato čísla provedou:
dz --> exp(it)*dz [toto ho pootočí kolem počátku o úhel t]
dz --> r*dz [toto ho "natáhne" o faktor r - de facto změna měřítka]
(můžete si to zkusit pro nějaké konkretní hodnoty, třeba t=?/3, r=2 a dz=0.1+0.2i)
Když to ty formulky teď přeložím do běžné češtiny, znamená to, že komplexní funkce se lokálně chovají jako pootočení následované rovnoměrným roztáhnutím. V tom předchozím příkladě (kurzívou) se dá lokální chování v okolí bodu z0 popsat tak, že daná funkce to okolí popadne, dvakrát ho přifoukne, pootočí o 60 stupňů a vlípne do bodu w0. Takto si jedním vrzem "osaháte" lokální akci vaší funkce f(z). Schematicky je to vyznačeno na dalším obrázku.
Všimněte si, že jak rovnoměrné roztáhnutí ("nafouknutí roviny"), tak pootočení zachovává úhly a to znamená, že pokud se dvě křivky ve vstupní rovině (ty šedé) protínají pod nějakým úhlem, na výstupu se budou protínat pod úhlem přesně stejným. Komplexní funkce s nenulovou derivací zachovávají úhly. Takovým zobrazením říkáme konformní a používají se např. v kvantové fyzice. Reálné funkce z roviny do roviny obecně tuto vlastnost postrádají a úhly zhusta deformují (tj. dvě křivky mohou mít na vstupu úhel 60° a na výstupu třeba 38° - hamba!). K takovéto politováníhodné události dochází v komplexní rovině pouze je-li derivace f'(z) = 0. Jinak jsou úhly vždy zachovány.
A to je také první náznak toho, že komplexní funkce nejsou nějaké nahrubo otesané nástroje, ale že jsou to naopak precisně seřízené mašinky.
+++++++++
Rovnice pro vedení tepla
Pochopit komplexní funkce - tedy jak vypadají a jak se chovají - nebyla nikdy snadná záležitost. Naštěstí pro nás - tápající amatéry i profesionály - se z hájemství fyziky vynořil nečekaný spojenec: rovnice pro vedení tepla. Určitě si ze základní školy pamatujete na experiment, kdy učitel zahřeje měděný drát nad hořícím kahánkem a k překvapení žactva vyjde najevo, že i v části daleko od plamene se teplota drátu postupně zvýšila. Teplo totiž dokáže proudit z jednoho místa na druhé.
Rovnice pro vedení tepla kvantitativně popisuje jakým způsobem se teplo rozvádí určitým prostředím. Je to poměrně komplikovaná parciální diferenciální rovnice, která ukazuje, jak se počáteční teplotní profil mění s časem. Nebudu vás děsit technickými podrobnostmi, ale odvolám se na praktickou zkušenost a selský rozum.
Teplo zpočátku proudí z teplejších míst do studenějších, ale po určité době dojde k vyrovnání rozdílů a nalezení ustáleného teplotního profilu (ekvilibria), které už se dále nevyvíjí. To ekvilibrium nemusí být nutně konstantní (závisí to na tzv. okrajových podmínkách). Pokud například jednu část drátu zahříváme a druhou ochlazujeme, po dosažení ekvilibria bude teplota v drátu stoupat od studenější části k teplejší lineárně, tak jak je znázorněno na dalším obrázku (ten počáteční teplotní profil jsem zvolil náhodně - drát je v některých místech studenější, v některých teplejší - ale nakonec tak či onak dojde k tomu výslednému ustálenému stavu).
Samozřejmě k vedení tepla dochází i ve dvou či ve třech dimenzích. Položte rozpálenou žehličku na kus plechu a zjistíte, že jeho teplota se zvýší i v místech, kde žehlička nestojí. Přenost tepla ve vyšších dimensích se řídí v podstatě stejnou rovnicí a stejně jako v jednodimensionálním případě vede k dosažení teplotního ekvilibria (ustáleného stavu).
Pokud necháte zapnutou žehličku na kusu plechu a odejdete na oběd, po návratu pravděpodobně zjistíte, že teplota plechu už se nemění - nejvyšší je přímo pod žehličkou a směrem od ní postupně klesá. Pro lepší představu jak takové vedení tepla vypadá se můžete podívat na video zde a nebo zde (na tom prvním videu si všimněte, jak tepelná konvekce okamžitě "vyhlazuje" jakékoliv lokální extrémy).
Z pohledu matematiky jsou ty ustálené teplotní profily reprezentovány (reálnými) tzv. harmonickými funkcemi. Ty sice v jedné proměnné odpovídají pouze lineárním funkcím, ale ve vícerozměrném případě mají velmi zajímavé vlastnosti.
A proč vám to říkám?
No protože se ukázalo, že když rozdělíme komplexní (holomorfní) funkci na reálnou a imaginární část (tak jako jsem to udělal v úvodu), tak ty dvě funkce, které takto dostaneme jsou obě harmonické - tedy reprezentují ustálené teplotní profily. Například funkce u(x,y) a v(x,y) z úvodu jsou obě harmonické a pokud si osu z představíte jako teplotu, můžete si to i fyzikálně interpretovat.
Přesněji: vyříznete-li si z komplexní roviny "kus plechu" - a na něm definujete teplotní profil jako reálnou nebo imagimární část libovolné komplexní holomorfní funkce f(z) - pak se váš plech bude nacházet v termálně ustáleném stavu a teplota se v něm už nebude dále měnit (za předpokladu, že kraje toho plechu budete držet na teplotě, kterou mají "předepsanou" funkcí f(z) - aby do něj nepřitékalo teplo zvenčí).
To, že komplexní (holomorfní) funkce jsou v podstatě složené ze dvou harmonických vede k tomu, že mají celou řadu překvapivých - až kouzelných - vlastností, které obecně definované reálné funkce nemají ani náhodou. Jako příklad se podíváme na tři vlastnosti.
1. Komplexní funkce nemají lokální maxima či minima - to znamená, že na jejich grafech nenajdete žádný "Říp" ani "propast Macochu". Z pohledu termodynamiky je to celkem pochopitelné. Uvnitř jejich definičního oboru se nemůže jen tak pro nic za nic kumulovat teplo. Nebo přesněji: pokud si vezmete komplexní funkci f(z) na nějaké oblasti P, pak je maxima absolutní hodnoty |f(z)| dosaženo vždy na hranici uvedené oblasti, nikoliv uvnitř (ještě přesnější formulace je zde). Reálné funkce takovouto vlastnost obecně nemají. Například reálná funkce u(x,y) = -x2-y2 má krásné lokální (i globální) maximum v bodě {0,0}. Taky to ale v žádném případě není funkce harmonická a nenajdete žádnou komplexní funkci jejíž reálná či imaginární složka by se s ní shodovala.
2. Komplexní funkce jsou zprůměrované v následujícím smyslu. Vezměme si nějakou funkci f(z) a kružnici se středem bodě z0. Pak hodnota funkce f(z) v tomto bodě - tedy f(z0) - se přesně rovná průměrné hodnotě té funkce na dané kružnici (podrobnosti zde). A to platí pro jakýkoliv bod a jakoukoliv kružnici se středem v tom bodě. Pro reálné funkce nic takového samozřejmě neplatí. Ty mohou mít v bodě {x0,y0} jednu hodnotu a průměr přes kružnici úplně jiný - viz výše zmíněná funkce u(x,y) = -x2-y2 v bodě {0,0}. Ta je na každé kružnici se středem v počátku záporná (a dokonce konstantní) zatímco v počátku samotném je nulová.
3. Komplexní funkce v libovolné oblasti se dají úplně zrekonstruovat z jejich hodnot na hranici (!). Představme si opět kus komplexní roviny jako plech, s tím že vám řeknu jakou hodnotu má moje funkce na okraji toho plechu. Vy si z těchto "hraničních" hodnot pak dokážete dopočítat jakoukoliv hodnotu té funkce uvnitř plechu (přesnější formulace zde). Z pohledu termodynamiky to opět není nic překvapivého. Pokud ten plech držíte na hranici v nějakém tepelně konstantním režimu (jeden okraj třeba nahříváte svíčkou a druhý chladíte ledem - tak pro tuto konfiguraci bude existovat pouze jeden ustálený teplotní profil a ten právě reprezentuje jednoznačně určené hodnoty naší funkce uvnitř plechu). Reálné funkce tuto vlastnost opět nemají - ty si pro dané hraniční hodnoty můžete uvnitř klidně promasírovat a pozměnit k obrazu svému. U komplexních vám ta masáž neprojde, protože byste tím masírováním zničili poměrně křehkou architekturu komplexních derivací.
To co byste si z této sekce měli odnést je, že komplexni funkce jsou velice rigidní a "neohebné" útvary, jejichž vnitřní struktura je velmi těsně provázaná. Může za to samozřejmě komplexní derivace, která na danou funkci klade podstatně vyšší nároky. Reálná derivace v podstatě říká, jak se funkce má chovat vpravo a vlevo. Komplexní derivace určuje její chování v nekonečně mnoha směrech a navíc tak, aby se výsledně jednalo o pootočení a rovnoměrné roztáhnutí (žádné deformace nejsou přípustné).
+++++++++
Analytické pokračování
U psychologických testů se občas setkáte s úlohou doplnit číslo do dané posloupnosti. To znamená, že musíte nejprve posloupnost podrobit analýze, vykoumat jak se chová a pak toto chování přirozeně prodloužit. Např.
1,2,4,8,16,32,... (doplníme 64 - mocniny dvojky)
1,0,-1,0,1,0,-1,0,1,0,-1,0,... (doplníme 1 - opakující se vzorec)
3,7,11,15,19,23,27,... (doplníme 31 - aritmetická posloupnost)
Samozřejmě při tom chceme, aby to prodloužení bylo jednoznačné (abychom předešli hádání se s porotou u vyhodnocení). Např. posloupnost 3,5,7... se dá rozšířit číslem 9 (lichá čísla) nebo 11 (posloupnost lichých prvočísel). Takovou bychom asi v testu nechtěli.
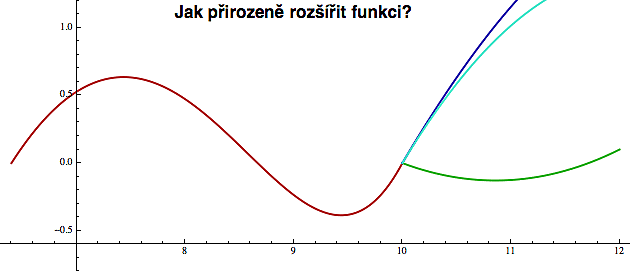
Když se podíváte na graf nějaké reálné funkce (třeba té červené na obrázku níže), můžete si ji představit jako posloupnost bodíků a zeptat se, zda existuje nějaké přirozené (a jednoznačné) rozšíření té funkce, které zachová všechny tendence, které její chování zatím projevilo.
Samozřejmě při tom rozšíření požadujeme, aby výsledná funkce byla hladká - tj. aby neměnila směr skokově (technicky: aby měla spojitou derivaci). Na základě požadavku hladkosti můžeme okamžitě vyloučit zelené pokračování. Takto si "přirozené rozšíření" funkce asi nikdo nepředstavuje.
Ovšem vybrat si mezi světle a tmavě modrým rozšířením je problém. V obou případech přejdeme z červené křivky do modré zcela hladce a bez jediného "drcnutí". Z toho je vidět, že u reálných funkcí požadavek hladkosti nestačí k tomu, abychom dokázali funkci jednoznačně rozšířit (tedy "prodloužit" její definiční obor). Dokonce se dá ukázat, že ani u reálných funkcí, které jsou nekonečně hladké (tj. mají spojité derivace všech řádů) to obecně nemusí vyjít, protože mocninné řady - které se při rozšíření používají - jsou v reálném případě trochu tvrdohlavé (podrobnosti zde).
To komplexní funkce jsou při rozšiřování jinačí kabrňáci. U nich požadavek hladkosti bohatě stačí k tomu, aby měly jednoznačně definované pokračování (a to se často používá pro zkoumání funkčních hodnot mimo oblast jejich přirozené matematické nebo fyzikální definice). Takže pokud někde v popelnici najdete pohozený kus komplexní funkce, doma si ji můžete kompletně zrekonstruovat a budete mít jistotu, že vám vyjde přesně ta původní (protože to rozšíření je jednoznačné). Je to tak trochu jako kdybyste v lese našli ocásek ještěrky a z něj si dokázali "doklonovat" celou ještěrku.
Jak ta rekonstrukce probíhá vidíme na dalším obrázku.
Představme si, že máme komplexní funkci definovanou na šedém pětiúhelníku uprostřed. Nejprve funkci rozvineme v mocninou řadu kolem nějakého vnitřního bodu z0 a součet té řady nám pak definuje hledané rozšíření. Jenom při tom musíme dávat pozor na póly naší funkce (tj. body, kde má funkce nekonečnou hodnotu - na obrázku třeba bod p). V nich totiž ta mocninná řada nemusí konvergovat. To se ale dá obejít (viz obrázek) tím, že si někde uvnitř toho zeleného kruhu, kde mocninná řada ještě stále konverguje, zvolíme jiný bod z1 a funkci rozvineme v další mocninnou řadu kolem toho nového bodu (a opět musíme dávat pozor na to, abychom se vyhnuli pólu). A takhle si postupně krůček po krůčku celou tu funkci opatrně zrekonstruujeme.
To, že je něco takového možné je opět dáno tím, že existence komplexní derivace klade na funkci velmi přísné podmínky. Hladkou reálnou funkci - tedy tu červenou křivku na předchozím obrázku - vám na tabuli nakreslí prakticky každé dítě, které umí udělat zvlněnou "čáru". Není to nic těžkého. Prostě mu vysvětlíte, že na té křivce nechcete vidět žádné "zuby" a máte hladkou funkci doma. Oproti tomu hladkou komplexní funkci jen tak "z ruky" nenakreslíte. Ta je tou svou derivací (tedy tím, že lokálně vypadá jako pootočení a roztáhnutí) příliš sešněrovaná a má příliš mnoho vnitřních vazeb. Ale právě díky nim se dá jednoznačně rozšířit, obvykle do celé komplexní roviny. A to je ten malý zázrak, kterému říkáme analytické pokračování.
+++++++++
Sekce jauvajs: komplexní derivace podruhé
pouze pro mimořádně otrlé povahy
Na samém začátku jsem vzal komplexní funkci f(z) a obratem ruky (přesněji rozepsáním proměnné z na reálnou a imaginární složku) z ní udělal dvě funkce reálné, u(x,y) a v(x,y).
Otázkou zůstává, zda se z každé dvojice reálných funkcí u(x,y) a v(x,y) dá "slepením" vytvořit funkce komplexní. Když si tedy spatlám nějakou funkci z roviny do roviny (tj. dva vstupy a dva výstupy), řekněme
G: {x,y} --> {x2-y3,3xy2+y} = {u(x,y),v(x,y)}
mohu ji považovat za komplexní funkci s komplexní derivací a se všemi těmi krásnými výše zmíněnými vlastnostmi, které z její existence vyplývají?
Odpověď je - jak asi tušíte - že zdaleka ne vždycky.
Aby to bylo jasnější, podíváme se na derivaci trochu obecnějším pohledem.
Zatím to pro nás bylo číslo č, kterým bylo nutno pronásobit přírůstek nezávisle proměnné dz, abychom dostali přírůstek závisle proměnné dw. Z pohledu vyšší matematiky je ale lepší se na derivaci funkce G v daném bodě z0 (o souřadnicích {x0,y0}) dívat jako na lineární zobrazení, které převádí přírůstek nezávisle proměnných {dx,dy} na ten "přibližný" (ve smyslu tečny) přírůstek závisle proměnných {du,dv} (samozřejmě, pokud je proměnná pouze jedna - ať reálná či komplexní - pak je to lineární zobrazení dáno předpisem x --> č*x a máme starou definici derivace).
Pro funkce více proměnných je takové lineární zobrazení (které derivace v bodě reprezentuje) určeno tzv. Jacobiho maticí J a ten převod přírůstků pak probíhá podle platných zákonů násobení matice a vektoru:
{du,dv} = J.{dx,dy}
kde J je matice parciálních derivací funkcí u a v, která je ve zkrácené notaci zobrazena na obrázku (1). A protože v textu by se mi s těmi znaky pro parciální derivace těžko zápasilo, budu níže používat symbolickou notaci (2) - tj. ux bude parciální derivace funkce u podle proměnné x atd.
Abychom zjistili, jak naše funkce G převádí {dx,dy} na {du,dv} v okolí nějakého konkretního bodu {x0,y0}, musíme ten bod nejprve dosadit do Jacobiho matice (tj. do všech těch parciálních derivací) a tím dostaneme normální číselnou matici (3), kde a,b,c,d jsou obecně 4 různá reálná čísla. Taková obecná matice může pochopitelně malé okolí daného bodu při přenosu různě deformovat.
A teď přijde důležité pozorování.
Výše jsme viděli, že komplexní funkce se lokálně chovají jako pootočení a "rovnoměrné roztáhnutí" (definované faktorem r). Rotační matice pro otočení v rovině o úhel t má známou formu (5).
Všimněte si, že členy na hlavní diagonále jsou stejné, zatímco ty na postranní mají opačné znaménko - a to se nezmění ani poté, co celou rotační matici pronásobíme číslem r (abychom do ní zahrnuli i to roztáhnutí). Tím se matice (5) převede na výsledný tvar (4), který v sobě zahrnuje obě operace.
Vyčíslená Jacobiho matice (3) se tedy bude chovat jako komplexní derivace pouze v případě, že d=a a c=-b a to v každém bodě.
Jinými slovy, ta Jacobiho matice musí mít v každém bodě formu (4). Jejím porovnáním s rovnicí (2) pak dostaneme, že parciální derivace našich funkcí u a v musí splňovat ux = vy a uy = -vx. A to je víceméně vše, co potřebujeme (až na nějaké technické drobnosti), abychom z reálných funkcí vytřískali funkce holomorfní.
Těmto podmínkám se říká Cauchy-Riemannovy podmínky a můžete si sami ověřit, že funkce F z úvodu je splňuje (a dá se proto chápat jako komplexní holomorfní funkce), zatímco funkce G z této sekce je nesplňuje a komplexní funkci z ní tedy neuděláme ani kdybychom se rozkrájeli.
Mimochodem to, že reálná i imaginární část komplexní funkce musí být harmonická se z těchto podmínek dá přímo odvodit.
+++++++++
Předpokládám, že čtenářům, kteří se pročetli až sem, odumřelo během produkce několik mozkových buněk a proto si na uklidnění a uctění jejch památky dnes dáme něco pietnějšího. Eva Pilarová: Rekviem.
Předchozí díly Matykání.
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
Jan Řeháček
Co rok dal

Začátek nového roku je tradičně příležitostí k ohlédnutí za rokem starým, takže jsem prohrábl archív a vylovil z něho pár fotografií z našeho parku, které si nenalezly cestu do některého z předchozích tématických blogů.
Jan Řeháček
Politické školení mužstva: Pyšná princezna

Roto končit! Pozor! (vejde útvarový politruk) Soudruzi vojáci, kapitál se potácí. Ale sám se nám na smetiště dějin nevypotácí. My mu musíme co, soudruzi? No? Nikdo? No, my mu musíme pomoci, vy hlavy hovězí!
Jan Řeháček
Ten podzim se nám hezky vybarvil

Každý podzim je v našem parku trochu jiný. Stromy, které by loni přešminkovaly i šestnáctku před prvním rande, jsou letos pobledlé jako Rusalka. A ty, které se zprvu barevně upejpaly, se najednou utrhly z řetězu. Jak řezníkův pes.
Jan Řeháček
Paroháčů je letos dost

Srnka je v našem parku jako houska na krámě. Zato setkání s jelenem si člověk musí považovat. Letos jsem ale náhodou objevil, kde se srocují: na záložním travnatém parkovišti, kterému se říká Gil's Hill, těsně před západem slunce.
Jan Řeháček
Chřadnoucí prales - pod vodou i nad ní

O korálovém útesu se říká, že je to "dešťový prales" oceánu. Biodiversita, kterou reprezentuje je ohromující. Totéž platí i o jeho suchozemském ekvivalentu. Bohužel, oba ekologické systémy se dostávají na seznam ohrožených druhů.
Jan Řeháček
Letní kvítí

Primární sezónou květů je sice jaro, ale ani léto není v našem parku z pohledu barev úplná nuda. Tady je malá fotovonička složená z příspěvků místní flory. Aneb kdo nekvete s námi, kvete proti nám.
Jan Řeháček
Plody léta

Léto je časem zrání a ani v našem parku tomu není jinak. Zajímavé plody nabízí říše rostlinná i živočišná. Tady je malý průřez letošní nabídkou: asijské maliny, kuriózní houby a malí mývalové. Ceny jsou mírné: léto létá zdarma.
Jan Řeháček
Kvetoucí fuga (Beethoven)

V Beethovenově Misse Solemnis nalezneme spoustu skrytých drahokamů, které zde leží prakticky nepovšimnuty, protože celková hudební struktura této Mše je na první poslech naprosto neprůstřelná. Jedním z nich je fuga v závěru Creda.
Jan Řeháček
Sovy a supi

V našem parku také poletuje spousta zajímavých ptáků. Tak jsem jich pár vyfotil. Sovy jsou sice nočními živočichy, ale na jaře se občas dají zastihnout i za denního světla. A za pár šupů k nim přihodím ještě pár supů. Ať nežeru.
Jan Řeháček
Vlčí západy

Při procházkách naším parkem občas fotím západy slunce z vyvýšeného travnatého parkoviště zvaného Gil's Hill. Říkám jim Vlčí západy. Jednak proto, že mají zhusta barvu vlčích máků a jednak proto, že náš park se jmenuje Vlčí past.
Jan Řeháček
Za devatero fotkami: Malebné peklo

Já to tušil, že jednou skončím v pekle. Jen jsem si představoval, že vstup bude mít z nějaké islandské sopky. Houbeles! Jeho vchod se nalézá poblíž vesničky Medkovy Kopce nedaleko Hlinska. "Lasciate ogne speranza, voi ch'intrate".
Jan Řeháček
Sedm divů jara

Po dlouhém barevném půstu zimní šedi působí návrat jarní kavalerie jako zjevení. V našem parku v tomto období kvete několik dřevin, s jejichž uměleckými kreacemi bych vás v tomto blogu rád seznámil. Matička příroda dokáže kouzlit.
Jan Řeháček
strž

V dnešním pokračování poetického cyklu "Bez básně a Hany" se nedozvíme jakou krevní skupinu mají nejraději novozélandští upíři a zda je tuna pampeliškového chmýří těžší než sbírka maturitních příkladů z matematiky.
Jan Řeháček
Devět zastavení času

Příroda se mění pomalu, ale jistě. Den ze dne nic nepostřehnete, ale když se na známá místa vrátíte za pár týdnů, naleznete desítky drobných změn. Tak jsem se na třech místech našeho parku devětkrát zastavil, abych je zachytil.
Jan Řeháček
Cesta do hlubin duše (Beethoven)

Lidská duše je odvěkou hádankou, na které si vylámaly zuby celé generace psychologů, teologů a filosofů. Tajuplný komplex uvnitř každého z nás. Pro mne je definicí lidské duše Beethovenův 14. smyčcový kvartet cis moll, op. 131.
| předchozí | 1 2 3 4 5 6 7 ... | další |
- Počet článků 402
- Celková karma 19,45
- Průměrná čtenost 920x