Matykání: jak funguje matematika
Už vás s tím Matykáním otravuju dost dlouho, tak je možná na čase, abych přiznal, jak k tomuto politováníhodnému nedopatření (které v našem podniku nastává maximálně jednou za 314 let) vlastně došlo.
Kdysi dávno, tuším na počátku roku 2014, jsem dostal email od jednoho čtenáře, zda bych nenapsal něco o dimenzi. Nu, co bych nenapsal. Lineární algebru si snad ze školy trochu pamatuju.
Ale hned mne taky napadlo, že pokud bych chtěl psát o dimenzi, měl bych nejprve říci něco o vektorech, tím pádem i o skalárech, a pravděpodobně také o reálných číslech jako takových. Zkrátka jsem si v hlavě sesumíroval takový malý plán útoku, jak se během 4-5 blogů k té dimenzi co nejrychleji propracovat.
Ale znáte to. To si takhle vyrazíte do hospody na jedno a pak se někde v časoprostoru nečekaně prohodí koleje a vy se vracíte domů v půl třetí ráno, hučku opentlenou fáborkama, v kapse nedojedenej kus tlačenky a ještě si k tomu na celou ulici vyřváváte "Má roztomilá Báruško...".
A tak jsme tady. 40 Matykání za náma a dimenze furt v nedohlednu. Ale nebojte - támhle v dáli, jak je ta zatáčka doprava, tak hned za ní už to bude.
+++++++++
Jak funguje matematika
Tradiční představa široké veřejnosti je, že matematik je vynikající počtář. To ale není úplná pravda. Moje osobní zkušenost je, že fyzici a inženýři umí počítat daleko lépe a rychleji. A to není zase tak úplně absurdní poznatek. Matematik v jistém smyslu tvoří nástroje a dobrý houslař nemusí být nutně houslový virtuos.
Možná ještě lepší analogií než hudební nástroje jsou nástroje pracovní. Kvantitativní vercajk je skutečnou doménou matematiky. Prakticky žádný vědec, technik či objevitel se neobejde bez výpočetních kladívek a šroubováčků, pomocí kterých se snaží smontovat objektivní zákonitosti našeho světa v nějaku funkční konstrukci. Ba i pilka se občas šikne. Matematika jim tyto nástroje nejen vyrábí, obrábí a kalibruje, ale ještě pro ně vyvíjí různé skříňky, poličky a šuplátka, aby se daly úsporně skladovat.
Základem matematického popisu světa je obvykle nějaká abstraktní struktura s přesně popsanými definičními vlastnostmi, která představuje kvantitativní model reality. Jako ukázku si můžeme připomenout pojem funkce.
Badatelé zkoumající náš svět si brzy povšimli, že mezi jednotlivými kvantitami existují určité vztahy. Matematika na poptávku po uchopení těchto závislostí zareagovala vytvořením pojmu funkce - tedy mechanismu, který převádí jedny hodnoty na druhé.
Jak jsme si již kdysi řekli, v té úplně základní verzi je funkce jakousi bedničkou, do které hodíte nezávisle proměnnou a na výstupu vám vyleze závisle proměnná.
Takto definovaný syrový polotovar ale příliš užitku nepřinese, protože nedokáže chování přiřazovacího mechanismu dostatečně zkrotit. Funkce obecná si skáče po definičním oboru jako splašený zajíc a nejeví žádné známky koherence (jako odstrašující příklad si můžete prohlédnout tzv. popcorn function, která je nespojitá ve všech racionálních číslech). Toto se podstatně rozchází s naší zkušeností, že většina procesů, na které v přírodě narazíme jsou spojité - tj. pokud jen malinko změníte vstup, na výstupu byste měli dostat také poměrně malou změnu.
Abychom tuto strukturu učinili použitelnou pro popis reálného světa, musíme jí dodat nějaké další vybavení - tj. naložit na ni určité podmínky, které jednak usměrní její chování a jednak nám umožní z nich odvodit další zákonitosti. Obecně platí, že čím silnější podmínky na danou strukturu (zde funkci) naložíte, tím zajímavější bude mít chování.
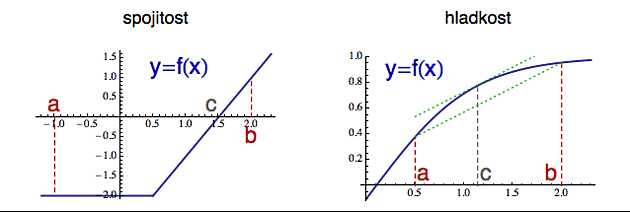
V tomto případě se hodí buď spojitost (funkční hodnota se nemění příliš rychle) a nebo - potřebujete-li silnější kafe - hladkost (směřování funkce - dané obvykle směrnem tečny ke grafu - se nemění příliš rychle). Na dalším obrázku si všimněte, že funkce vlevo je sice spojitá, ale není hladká. V tom bodě, kde má její graf "zub" se směr funkce mění skokově.
Tímto jsme v chaotickém vesmíru funkcí vytvořili dvě přesně definované škatulky, které nám umožní zkoumat další vlastnosti - tedy odvozovat je z těch definičních nebo již dříve dokázaných (proto je matematika v jistém smyslu "kupčením s vlastnostmi"). Není potřeba pracně objevovat Ameriku pro každou novou funkci, se kterou se v aplikacích setkáme. Čím jemnější škatulky máme, tím přesněji jsme schopni popsat, co funkce v nich obsažené dokážou. Proto máme kromě výše uvedených také funkce omezené, monotónní, absolutně spojité, lipschitzovské, s konečnou variací, diferencovatelné, měřitelné, neplacené, doživotní atd. Pro každou konkretní funkci pak už stačí jen zjistit v jaké škatulce se nalézá a hned se o ní dozvíme spoustu zajímavých informací.
K nejdůležitějším vlastnostem spojitých funkcí (vlevo) např. patří tzv. Bolzanova věta, která nám říká, že pokud mají hodnoty spojité funkce v bodech a a b různé znaménko, pak někde mezi nimi musí ležet hodnota c, kde je funkce rovna nule (má zde tedy kořen). To je z principu jasné. Spojité funkce mají graf, který lze nakreslit bez zvednutí tužky, takže máme-li se dostat ze záporné hodnoty do kladné, někde mezi a a b tu nulu přelézt musíme (nelze ji "přeskočit"). Všimněte si, že Bolzanova věta nám neříká, kde tu nulu přelezeme. To ani nemůže, protože různé typy funkcí ji přelezou v různých bodech. Ona vám pouze zaručí, že někde mezi a a b ten kořen skutečně je. Tomuto typu výsledků se říká "existenční věta". A nutno přiznat, že prakticky založené typy přivádí k šílenství: půl roku počítáte proudění tepla olověnou deskou a když se - zamotaní do parciálních diferenciálních rovnic - dopotácíte k všemocnému matematikovi, ten vám ještě nasype sůl do ran, když tajemně zamumlá něco jako "v Sobolevově prostoru W4,2 existuje jednoznačné řešení, ale spočítat si ho musíte sami".
(humorná vložka): Inženýr, fyzik a matematik se ubytují v hotelu a co čert nechce, v noci je vzbudí požár. Inženýr nezaváhá, doštrachá se do koupelny, otočí kohoutkem a poté co valící se voda zaplaví oheň, jde spát. Fyzik se probudí, spočítá si měrné teplo materiálu v jeho pokoji, do kbelíku napustí přesný objem vody a poté, co oheň bez vyplýtvání jediné kapky uhasí, jde spát. Matematik se mrkne do předsíňky, na stěně zmerčí hasicí přístroj, zapíše si do notýsku "řešení existuje" a jde spát.
Protože hladkost (neexistence "zubů" na grafu) je silnější podmínka, hladké funkce splňují to, co spojité (např. Bolzanovu větu), ale mají pár zajímavých vlastností navíc. Pokud si například spojíte body a a b sečnou (zeleně na obrázku vpravo), pak z hladkosti dostanete existenci bodu c (mezi a a b), kde má tečna přesně stejnou směrnici jako ta sečna. To na první pohled vypadá jako další zcela neužitečná hříčka, kterou si může vymyslet jen znuděný pašerák kružítek při výkonu 30 letého trestu, ale tento výsledek (říká se mu věta o střední hodnotě) je teoretickým základem rozvoje funkcí do nekonečných polynomů (Taylorovy řady) a dalších aplikací diferenciálniho počtu. U funkce vlevo takovou tečnu nenajdete, právě kvůli tomu "zubu".
Ta formalizace struktur je však trochu dvousečný meč. Na jedné straně nám umožňuje efektivně popsat vlastnosti nesmírně širokých tříd funkcí, takže se pak při dokazování existence kořene nebo určité tečny nemusíte zvlášt babrat se sínem, zvlášť s kosínem a zvlášť s logaritmem, natož pak s jejich kombinacemi, ale zvládnete to všechno jedním vrzem. Na druhé straně tím, že jste konkretní formu vaší funkce zahalili abstrakcí, tak dostanete pouze existenční větu a chcete-li ten kořen skutečně najít, musíte se k té konkretní funkci vrátit a použít nějaký specifický nástroj (třeba kvadratickou nebo kubickou formulku, popřípadě poměrně univerzální Newtonovu metodu).
+++++++++
Matematika se samozřejmě snaží dívat přírodním vědám přes rameno a otipovat o jaké typy abstraktních struktur by asi tak mohl být zájem. Pozoruje jejich postupy a snaží se vyhmátnout, co mají společného. Ale výsledně se musí od konkretností odpoutat a obléknout své závěry do abstraktního kabátu, aby mohla vyhovět všem. Ta samá matice, která slouží ekonomům, musí posloužit také jaderným fyzikům. A pokud to, co hledáte, není zrovna na skladě, nevadí. Nenápadně zajdete se svými požadavky do kumbálu za hlavním skladem: "Zdravíčko, šéfíku - potřeboval bych něco na algebru, ale taky aby to umělo spojitost". A matematik si posune kostěné brýle na mys nosu a spiklenecky vám sdělí, že by tady pod pultem měl jednu takovou lokálně kompaktní topologickou grupu, prvotřídní kvalitka.
Občas se samozřejmě stane, že matematik se nechá unést vlastní představivostí a vymyslí strukturu, která neslouží žádné přímé aplikaci, ale vznikla prostě dalším rozvíjením již známého objektu. Něco ve stylu - "hele a co by se stalo, kdybychom semka dali baterku a tady ty dvě hřídele spojili táhlem". Ne vždy z toho vznikne smysluplný nástroj a když si projdete matematické časopisy z minulého století, najdete v nich spoustu vymyšleností, které se jednoduše neuchytily. Tu kladívko s vestavěným otvírákem, tamhle kleště pro třírukou opici. Ale takový je život. Když vznikla komplexní čísla, většina vědecké obce na ně pohlížela jako na výplod choré mysli. A vidíte - nakonec stala se základem kvantové mechaniky. Člověk prostě nikdy neví, co se jednou bude hodit.
Kvantová mechanika se - shodou okolností - zasloužila také o rozvoj vektorových prostorů a discipliny, která se jimi podrobně zabývá, tedy lineární algebry. Dříve než se do nich zakousneme, chtěl bych ale poznamenat, že v matematice se slovo "prostor" používá v poněkud širším smyslu pro označení nějaké strukturované množiny, tj. pro vyznačení "hřiště", na kterém si budeme hrát (topologický prostor, metrický prostor, funkční prostor, pravděpodobnostní prostor atd). Nemusí to tedy nutně být ten důvěrně známý 3D prostor, ve kterém žijeme.
+++++++++
Vektorové prostory
Vektory se zrodily z poznání, že některé fyzikální veličiny (například rychlost nebo síla) mají nejen určitou velikost, ale také konkrétní směr. Proto si je fyzici znázorňují pomocí šipčiček, které se dají přirozeným způsobem sčítat (skládat) a násobit skaláry, což jsou veličiny, které směr nemají a jsou tedy pouhými čísly. Pokud na nás působí síla F1 a současně síla F2, pak náš pohyb bude určen výslednou silou F = F1 + F2 (součet). Bude-li působící síla ve stejném směru a my jen pořádně přitlačíme na pilu, řekněme dvakrát, geometricky dostaneme tu samou šipčičku, jen dvakrát delší, tedy 2F (skalární násobek).
V rovině R2 odpovídají vektory dvojicím reálných čísel, v prostoru R3 pak trojicícím. Obecněji, v tzv. eukleidovském prostoru R^n odpovídají n-ticím. Studenti se často ptají, jaký je rozdíl mezi vektorem a bodem (oba jsou reprezentovány pomocí n-tic čísel). Velký rozdíl mezi nimi není - je to jen věc interpretace. Vektor je v podstatě bod, který si ve formě šipčiček nese svůj vlastní počátek s sebou (tak jako si hlemýžď nese svůj vlastní domeček) a dá se tudíž lépe sečíst ("složit") s ostatními body/vektory. Prostě ten svůj pohyblivý počátek přiloží na konec předchozího vektoru. Pokud vás zajímají spíše statické geometrické vlastnosti, dívejte se na n-tici jako na bod. Pokud vás zajímají dynamické algebraické vlastnosti, pohlížejte na ni jako na vektor.
Následující obrázek ukazuje jednoduché složení (součet) vektorů v rovině i prostoru.
Pravidla pro počítání s takovými objekty se podobají jako vejce vejci. Nemá tedy smysl, vytvářet pro každé n zvláštní teorii pro počítání s šipčičkami, ale vyplatí se vymyslet abstraktní algebraickou strukturu, která z chování studovaných příkladů vytáhne podstatné rysy a zakóduje je do přesně specifikovaných zákonů.
Výsledkem takového snažení je struktura, které říkáme "vektorový prostor" a v té nejobecnější formě si ho můžete představit jako "pytel objektů", které se dají navzájem sčítat a násobit skaláry (záměrně neříkám "množina", protože při těch vedrech za okny by takové slovo mohlo s jemnějšími povahami seknout). Stejně jako u funkcí se pak další vlastnosti neodvozují z konkrétních příkladů, ale z definičních vztahů, které jsme z nich vyždímali abstrakcí.
Těmi vektory mohou být nejen n-tice čísel (šipčičky), ale třeba i matice, polynomy nebo funkce. Zkrátka cokoliv se dá sčítat a skalárně násobit. Jediné, co musíte zaručit je, že operace na těchto objektech definované splňují příslušné podmínky. Pokud se vám podaří ty operace definovat pro nudle, budete mít vektorový prostor z nudlí. A jak asi čekáte, ani skaláry se nevyhnuly "abstraktizaci". Přestože v drtivé většině případů jsou jimi reálná čísla a v drtivé většině zbývajících případů jsou jimi komplexní čísla, obecně pochází skaláry ze zvláštní algebraické struktury zvané "pole", která v podstatě kodifikuje chování toho, čemu v matematice říkáme čísla.
(kdo ovládá objektové programování, tak si jistě všiml, že matematika v podstatě nahrazuje konkretní objekty přesně definovanými funkčními specifikacemi, kterým se říká "interface" - tedy neváže se na speciální příklady (implementace), ale jen říká, jaké vlastnosti ta či ona struktura má)
První otázka, kterou zvídaví studenti při setkání s vektorovými prostory kladou je proč se tyto objekty (vektory) také nedají mezi sebou násobit. Proč se dají pouze sčítat a násobit skaláry? Odpověď je, že v některých případech se násobení těchto objektů navzájem skutečně definovat dá. Pak ale vznikne struktura, která je o něco bohatší (komplikovanější) než "vektorový prostor" a říká se jí "algebra". V ní můžete objekty nejen sčítat a násobit skalárem, ale také násobit mezi sebou (klasickým příkladem jsou matice). V mnoha užitečných případech se ale to násobení nedá smysluplně definovat a proto v aplikacích převládají vektory.
Vektorový prostor je tedy abstraktní pojem, který nejenže umožnil jednotné studium všemožných "šipčiček" pod jednou střechou, ale ještě ukázal, že stejným způsobem se dá přistoupit i k jiným, daleko komplikovanějším pojmům (funkce, polynomy, matice) a vrhnout na ně nové světlo.
Na rozdíl od přírodních věd si matematika nemusí lámat hlavu s reálnými experimenty, takže je ušetřena řádění živlů jako jsou tření, přílišná vlhkost vzduchu nebo tvrdohlavost laboratorních myší. Namísto hmotných předmětů a nevyzpytatelných organismů pracuje s idealizovanými objekty, definovanými pomocí zcela sterilních vlastností. Matematik neřekne "pták usedl na větev", ale "opeřený objekt, který třepotá křídly a dělá píp, usedl na válcovitou dřevěnou strukturu z níž vybíhaji isomorfní podstruktury". Vše je milosrdně skyto pod rouškou abstrakce.
+++++++++
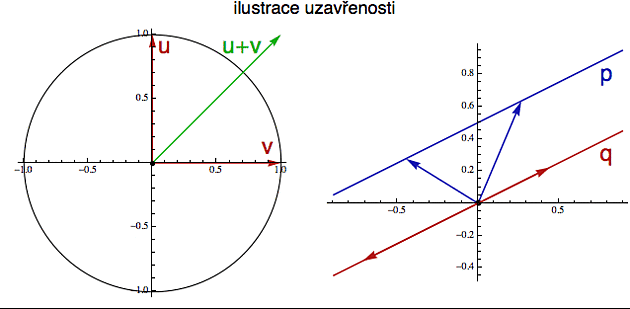
Závěrem této sekce se zmíním o jedné vlastnosti, která je většinou schovaná v "jemném tisku" definic. Pokud máte v matematice nějakou množinu objektů se kterými si chcete "hrát", je důležité, abyste při tom "hraní" z příslušné množiny nevypadli. To znamená, že sčítáte-li třeba nějaké objekty, je důležité, aby výsledek takového sčítání byl opět v původní množině. Tomuto principu se říká "uzavřenost" a často hraje důležitou roli při rozhodování, zda vaše struktura splňuje nebo nesplňuje definiční podmínky.
Fyzici by se nám asi pěkně poděkovali, kdybychom jim dali vektorový prostor brambor a při prvním pokusu dvě brambory sečíst by dostali ananas. Naštěstí v reálném životě si s tím většinou nemusíte lámat hlavu, protože struktury, které vám matematika předá jsou ve smyslu uzavřenosti "vytuněné".
Jako "nevytuněný" příklad si vezměme množinu všech polynomů přesně prvního stupně (tj. tvaru ax+b, kde a je nenulové číslo). Ty se dají krásně sčítat i násobit skalárem, ale vektorový prostor netvoří, protože při jejich součtu můžeme dostat polynom nultého stupně: (x+2) + (-x+1) = 3. Konstantní polynom p(x)=3 tedy "vypadl" z našeho "skoro vektorového prostoru".
I se šipčičkami musíme být opatrní. V rovině můžeme například uvažovat vektory (body) ležící na kružnici. I ty se dají sčítat a násobit skalárem, ale kružnice sama o sobě vektorový prostor netvoří, protože při součtu dvou takových vektorů se můžeme lehce dostat mimo kružnici (viz obrázek). A při skalárním násobku totéž.
Dokonce ani přímky nejsou úplně z obliga. Na obrázku vpravo bude červená přímka v pohodě, protože vektory z ní vytažené se po součtu vrátí zpět do té samé přímky, U modré to očividně neplatí. Když sečtete ty dva naznačené vektory, tak se ocitnete daleko "za přímkou". Proto se z ní nedá udělat vektorový prostor.
Pokud se část již prověřeného vektorového prostoru sama o sobě chová jako vektorový prostor (a specielně je-li uzavřená vzhledem k operaci sčítání a skalárního násobení), pak o té množině říkáme, že je podprostorem. V rovině R2 jsou podprostorem všechny přímky procházající počátkem, v prostoru R3 pak navíc i všechny roviny procházející počátkem.
+++++++++
Nezávislost
V diskusích existují dva typy lidí. Jeden typ přináší nové informace či pohledy na věc, ten druhý jen reformuluje předchozí myšlenky, splácává již vyřčené, kombinuje to, co už dávno leží na stole. I v lineární algebře se snažíme odlišit "zásadně nové" vektory od těch, které se dají vygenerovat z vektorů již popsaných.
Tato snaha - ležící v samotném srdci pojmu dimenze - nás dovede ke studiu nezávislosti vektorů. Na počátku takového úsilí kupodivu není slovo, ale lineární kombinace.
Jak jsme si řekli, vektorové prostory se skládají z objektů, které lze sčítat a násobit skaláry. Máme-li tedy řekněme 4 vektory T, U, V, W, pak nejobecnější objekt, který si z nich můžeme sestrojit pomocí definovaných operací se zove lineární kombinace a pro naši čtveřici vypadá takto:
tT + uU + vV + wW
(kde t,u,v a w jsou libovolné skaláry)
Je dobré mít na paměti geometrickou intuici. Např. pro dva vektory U a V budou jejich lineární kombinace (pro všechny možné páry skalárů) tvořit rovinu těmito vektory určenou (nebo v nejhorším případě přímku, pokud mají oba vektory stejný směr).
Samozřejmě občas se stane, že nějaký vektor je lineární kombinací jiných vektorů. Např. je-li
U = (2,1,0,1)
V = (-1,0,0,-1)
W = (1,2,3,1)
definujeme T=2U+V-W a dostaneme T=(2,0,-3,0).
Vektor T je zde kombinací vektorů U, V a W.
Vektor, který je pouhou kombinací jiných vektorů, je na nich přirozeně závislý. Je tu ale jeden terminologický háček. My bychom si z té rovnice mohli vyjádřit vektor W = 2U+V-T a stejně dobře tvrdit, že vektor W je závislý na vektorech U, V a T (a podobně pro zbylé vektory U a V, které by se tímto závisláckým opomenutím mohly cítit diskriminovány). A tak to nakonec matematici politicky korektně vyřešili tak, že všechny vektory naházeli na jednu stranu
2U + V - W - T = 0
A je to. Nikdo není znevýhodněn.
Dané vektory pak prohlásili za lineárně závislé, pokud se dá najít netriviální lineární kombinace těchto vektorů, která nám dá nulový vektor (zde 0 = (0,0,0,0)). A my takovou máme. To slůvko netriviální je velmi důležité a znamená, že ne všechny skaláry v té kombinaci jsou nula (pomocí nulových koeficientů bychom si ten nulový vektor mohli nabrnkat triviálně a taková definice by postrádala smysl).
Lineární nezávislost vektorů se definuje opačně, ale ve stejném duchu (tedy žádný vektor nebude mít privilegované postavení na jedné straně rovnice). Vektory U1, U2, ... Um budou lineárně nezávislé, pokud jediná lineární kombinace těchto vektorů, která nám dá nulový vektor je ta triviální.
To znamená, že z rovnice
u1 U1 + u2 U2 + ... + um Um = 0
vyplývá, že všechny neznámé koeficienty musí být nula, tj.
u1 = u2 = ... = um = 0
+++++++++
V některých případech se dá lineární (ne)závislost odhadnout od oka.
Např. dva vektory jsou závislé právě tehdy, jsou-li kolineární - leží tedy v jedné přímce a jejich složky musí být ve stejném poměru:
U = (1,2,3,4,5) a V=(3,6,9,12,15)
jsou závislé, protože V=3U neboli (politicky korektně) V-3U = 0. Bez velkého počítání tady hned vidíme tu netriviální kombinaci, která nám dá nulový vektor 0=(0,0,0,0,0).
Tři vektory budou závislé pokud leží v jedné rovině (přímku už uvažovat nebudeme) a to se prostým okem vždy poznat nedá. Co třeba následující trojice vektorů z R3. Závislé nebo nezávislé?
U = (-1,4,1)
V = (0,-1,2)
W =(-3,10,7)
Dokážete od oka poznat, zda leží v jedné rovině? Tady nezbývá, než začít počítat.
Obecný postup je celkem jednoduchý (i když často pracný). Prostě si napíšeme lineární kombinaci daných vektorů, která dává nulový vektor a začneme ji řešit (tedy hledat neznámé koeficienty u,v, a w). Pokud se nám podaří najít nenulové (netriviální) koeficienty, vektory jsou závislé. Pokud jediné řešení bude u=v=w=0, pak jsou vektory nezávislé. Tak do toho.
u*(-1,4,1) + v*(0,-1,2) + w*(-3,10,7) = (0,0,0)
Tuto vektorovou rovnici si můžeme (po složkách) rozepsat na soustavu rovnic a pustit se do řešení (libovolnou metodou)
-u-3w = 0
4u-v+10w = 0
u+2v+7w = 0
Asi deset minut se z nás kouří (jak že se dělá ta Gaussova eliminace?) a nakonec nalezneme řešení u=3, v=2, w=-1 (ono je jich nekonečně mnoho, ale jedno netriviální nám zde bohatě stačí). Tyto vektory jsou lineárně závislé, protože jsme nalezli jejich netriviální kombinaci, která dává nulový vektor.
Tahle metoda funguje vždy, ale ruku na srdce - řešit rovnice je docela otrava - takže v mnoha speciálních případech můžete (ne)závislost vyšetřit snadněji pomocí pokročilých metod z teorie matic nebo geometrie (tedy pokud je máte v malíčku nebo alespoň v prsteníčku - nikoliv však v paži). V tomto případě můžete např. naházet všechny tři vektory do matice - její determinant vám vyjde nula a závislost vám spadne do klína téměř zadarmo. A nebo si pomocí vektorového součinu spočítáte kolmici na vektory U a V (což je UxV = (9,2,1)) a zjistíte, že i zbývající vektor W je ni kolmý a leží tudíž ve stejné rovině jako U a V. Všimněte si, že v obou těchto vychytávkách tu kombinaci explicitně vůbec neuvidíte. Oddře to za vás teorie.
+++++++++
Geometrické příslušenství
Ta základní struktura vektorového prostoru je sice definována poměrně obecně, ale pro většinu aplikací si vystačíte s klasickou představou "šipčiček" v rovině s oběma operacemi definovanými klasicky "po složkách", tedy:
je-li u=(2,3,1), v=(-1,0,1)
pak u+v = (1,3,2), u-v = (3,3,0), 2u = (4,6,2), -5v=(5,0,-5) atd.
S tak primitivní strukturou se ale moc psích kusů dělat nedá. Maximálně s ní můžete řešit soustavy lineárních rovnic (ty vektory si ale budete muset vyrovnat do matice).
Pokud budeme chtít vektory použít pro geometrické úvahy - což se přímo nabízí, vzhledem k tomu, že odpovídají bodům v rovině, prostoru či vyšších ekvivalentech - bude potřeba k té základní struktuře něco přidat (jako jsme to udělali u funkcí). Musíme vektory naučit dvě věci. Za prvé, jak měřit vzdálenosti mezi dvěma body (vektory) a za druhé jak měřit úhly mezi dvěma směry (vektory).
Matematika nám pochopitelně neřekne přímo, jak to udělat, ale zavede do vektorových prostorů dvě abstraktní funkce (s přesně specifikovanými vlastnostmi), které nám umožní tyto úlohy vyřešit - s tím, že konkretní implementace bude záviset na daném problému (jsou vektorové prostory, kde se ty funkce dají zavést několika možnými způsoby).
První funkcí je tzv. norma (její vlastnosti si můžete prostudovat zde). Ta každému vektoru u přiřadí nezáporné reálné číslo ||u||, které si můžete představit jako jeho délku. Norma vektoru je zobecněním absolutní hodnoty čísla a tomu odpovídá i značení - místo svislých čar používáme svislé dvoučáry.
Pro klasické vektorové prostory šipčiček (tedy n-tic reálných čísel) se většinou definuje tzv. standardní eukleidovská norma, která je v podstatě odvozena ze zobecnělé Pythagorovy věty:
||u|| = sqrt(u12+u22+...un2), kde u=(u1,u2,...,un)
takže například pro
u=(2,3,1) dostaneme ||u||=sqrt(14).
Pro dva body, odpovídající vektorům u a v, se pak jejich vzdálenost definuje jako d(u,v)=||u-v||. Vzdálenost dvou bodů tedy dostanete tak, že odečtete jejich polohové vektory a spočítáte normu výsledného rozdílu.
+++++++++
Druhou geometrickou funkcí je skalární součin, což je - jak název napovídá - v podstatě operace mezi dvěma vektory jejímž výsledkem je skalár. Můžeme se na ni dívat jako na funkci, která každé dvojici vektorů přiřadí výsledek tohoto součinu. Značí se buď tečkou mezi dvěma vektory (viz v angličtině "dot product") a nebo závorkami. Pro dva vektory u a v vypadá takto
u.v nebo (u,v) nebo dokonce <u,v>
Implementace opět závisí na konkrétním prostoru, ale pro tradiční n-složkové šipečky u=(u1,u2,...,un) a v=(v1,v2,...,vn) se definuje jednoduše:
(u,v) = u1*v1+u2*v2+...+un*vn = u.v
(tj. vynásobíte odpovídající si složky a pak tyto součiny všechny posčítáte)
Jakmile máme na vektorovém prostoru zaveden skalární součin, úhel t mezi dvěma vektory u a v je definován pomocí kosínu:
cos(t) = u.v / ||u|| * ||v||
takže např. pro rovinné vektory u=(-1,3) a v=(1,1) dostaneme pro úhel t
cos(t) = 2 / sqrt(10) * sqrt(2) = 2 / sqrt(20) = 0.447
a tedy t = 1.107 (radiánu), což je bratru t = 63°.
(můžete si to vykreslit na čtverečkovaný papír a přeměřit úhloměrem)
Důležitým speciálním případem je situace, kdy je u.v = 0. Pak je úhel roven 90° a vektory jsou kolmé (neboli ortogonální).
Jakmile máme definován úhel mezi vektory, můžeme měřit i úhly mezi přímkami a dalšímy objekty (jen je třeba dbát na konvence - úhel mezi přímkami musí být menší než 90). Jako jako cvičení si rozmyslete, jak se mění úhel mezi vektory u=(1,0) a v=(cos(t),sin(t)), kde t je reálné číslo.
+++++++++
Velmi zajímavá otázka je, zda musíte do vektorového prostoru dodat oba tyto doplňky zvlášť a nebo zda se jeden dá odvodit z druhého.
Norma vektoru se vždy dá odvodit ze skalárního součinu (se sebou samým):
||u|| = sqrt(u.u)
(to znamená, že jakmile umíte měřit úhly, umíte měřit i délky)
Naopak je to trochu horší, ale v tom nejjednodušším případě Eukleidovských prostorů si skalární součin můžeme vytvořit z normy pomocí tzv. polarizační identity, která pro reálné prostory vypadá takto:
(u,v) = (||u+v||2 - ||u-v||2) / 4
(pro komplexní prostory si tu identitu můžete najít zde)
Úplně obecně to ale neplatí - měření úhlů je o něco zapeklitější problém než měření délek a ne vždy se dá skalární součin nabrnkat z normy výše uvedeným způsobem. K tomu se časem vrátím, až se dostaneme do nekonečné dimenze.
+++++++++
Sekce Jauvajs: projekce
(jen pro mimořádně otrlé povahy)
Stojíte-li na sluníčku, uvidíte za sebou stín. Z pohledu matematiky je to projekce jednoho vektoru (vaší osoby) do jiného vektoru (tečny k povrchu Země).
Projekce je typ zobrazení (transformace) na vektorovém prostoru - tj. funkce, kde vstupem i výstupem je nějaký vektor. Jak je v kraji zvykem, v abstraktní rovině není definována konkretním vzorečkem, ale jako zobrazení, které má následující pozoruhodnou vlastnost: P(P(x))=P(x). To znamená, že projekce složená sama se sebou je stále to původní zobrazení. Té vlastnosti se mimochodem říká "idempotence" (co jsme se tomu na matfyzu nahihňali). Když opakovaně provádíme různá zobrazení, obvykle dostaneme posloupnost iterací (tohoto zobrazení). Projekce je "konečná" - tu můžeme iterovat jak mourovatý a nic dalšího už z ní nevytřískáme. Lidově řečeno - stín stínu zůstane tím samým stínem.
Projekcí je v matematice celá řada, ale abychom se neutopili v abstraktní bramboračce, podíváme se jen na tu nejdůležitější.
Pravoúhlá pojekce má velký význam ve fyzice, protože u mnoha vektorů nás nezajímá jeho velikost jako spíš projekce do nějakého určitého směru (tj. jak velká část daného vektoru v tom směru působí). Například z gravitační síly G sněhového kvádru S na nakloněné střeše domu nás zajímá "normálová" složka Fn působící kolmo na povrch střechy (což je projekce - viz obr. vpravo).
Uvažujme nejprve dva vektory u a v (jako na obrázku vlevo) a zeptejme se, jak velký bude pravoúhlý "průmět" (projekce) vektoru u do vektoru v. To znamená, že posvítíme baterkou tak, že paprsky budou kolmé na vektor v a podíváme se, jak dlouhý bude stín u (zde délka úsečky OV) na podlaze dané vektorem v.
Při projekci musíme dávat pozor, co promítáme do čeho. Projekce vektoru v do směru u by vyšla trochu jinak.
Protože promítáme pravoúhle, můžeme použít goniometrické funkce. Přepona pravoúhlého trojúhelníku OVU je délka vektoru u a to, co nás zajímá, je délka přilehlé odvěsny OV, takže dostaneme
cos(t) = OV / ||u||
Z definice úhlu mezi vektory (pomocí skalárního součinu) máme
cos(t) = u.v / ||u|| * ||v||
a tedy
OV = u.v / ||v||
Pokud promítáme do jednotkového vektoru v (což se dá zařídit tak, že ho vydělíme jeho normou), pak skalární součin nám přímo udává velikost průmětu jednoho vektoru do druhého.
Na procvičení: je-li u=(2,2) a v=(4,-1), pak velikost projekce u do v je OV=6/sqrt(17)=1.455, což je zhruba polovina délky vektoru ||u||=2.828. Velikost projekce v do u by byla 6/sqrt(8)=2.121.
+++++++++
A teď zpátky k obrázku vpravo: pokusíme se vektor síly G = (0,-1) rozložit na složku normálovou Fn, která tlačí na střechu, a složku tečnou Ft, která ukazuje kudy teče voda. Střecha má sklon určený tečným vektorem (-1,-2), což znamená, že její úhel t = 63.43° (tan(t)=2). Ale to jen tak pro zasmání.
Označme si jednotkové vektory ve směru tečny a normály:
Ft = a*(-1,-2)
Fn = a*(2,-1)
Tu normálu jsem dostal z podmínky kolmosti (skalární součin musí být nula) a konstanta a=1/sqrt(5) je normalizační faktor, který udělá z obou vektorů jednotkové (aby se nám ten průmět vektoru G v obou případech z OV rovnice lépe počítal).
Dostaneme
G = gt*Ft + gn*Fn
kde gt a gn jsou velikosti průmětů vektoru G do vektorů Ft a Fn:
gt = G.Ft = 2/sqrt(5) = 0.894
gn = G.Fn = 1/sqrt(5) = 0.447
Normálová síla (která zatěžuje střechu) je tedy zhruba poloviční, což je způsobeno velkým sklonem, takže gravitační síla působící směrem dolů se z velké části "svede" do tečného vektoru a odteče pryč.
+++++++++
A protože to dneska byla taková všehochuť, dáme si na vydýchání jednu hudební - a hezky s ilustracemi. Genesis: Supper's Ready.
Předchozí díly Matykání
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
| Další články autora |
Tři roky vězení. Soud Ferimu potvrdil trest za znásilnění, odvolání zamítl
Městský soud v Praze potvrdil tříletý trest bývalému poslanci Dominiku Ferimu. Za znásilnění a...
Moderní lichváři připravují o bydlení dlužníky i jejich příbuzné. Trik je snadný
Premium Potřebujete rychle peníze, pár set tisíc korun a ta nabídka zní lákavě: do 24 hodin máte peníze na...
Takhle se mě dotýkal jen gynekolog. Fanynky PSG si stěžují na obtěžování
Mnoho žen si po úterním fotbalovém utkání mezi PSG a Barcelonou postěžovalo na obtěžování ze strany...
Školu neznaly, myly se v potoce. Živořící děti v Hluboké vysvobodili až strážníci
Otřesný případ odhalili strážníci z Hluboké nad Vltavou na Českobudějovicku. Při jedné z kontrol...
Prezident Petr Pavel se zranil v obličeji při střelbě ve zbrojovce
Prezident Petr Pavel se při střelbě na střelnici v uherskobrodské České zbrojovce, kam zavítal...
Rusové hlásí průlom fronty. Ukrajinská minela jim přihrála klíčové město
Premium Jako „den průlomů“ oslavují ruští vojenští blogeři pondělní události na doněcké frontě, kde se...
Ve vaně mi spí cizí muž, nejde vzbudit, volal na policii zoufalý majitel domu
Policisté na Havlíčkobrodsku vyšetřují neobvyklý případ. Do domu v Úsobí se v úterý večer...
Naučená omluva, bez upřímné lítosti. Za pokus o vraždu dívky dostal Ukrajinec 19 let
Krajský soud v Plzni odsoudil na devatenáct let Ukrajince Viktora Veselovského, který se loni v...
Svobodu se lidovci snažili dostat pryč ze strany, teď kauzu odkládají
Lidovecká snaha vystrnadit ze strany jednoho ze svých nejznámějších poliků, bývalého šéfa strany a...

Instalatér do Německa
Arcon Personalservice GmbH
nabízený plat:
75 260 - 90 320 Kč
- Počet článků 402
- Celková karma 19,54
- Průměrná čtenost 920x