Růžičky z Riemannovy zahrádky
(řeknu to hned a na rovinu: tohle bude asi jen pro otrlé povahy)
Pokud bude něco nejasné, doporučuji navštívit starší Matykání o Zeta funkci, komplexní exponenciele a nekonečných řadách.
Pro reálné číslo s>1 je Zeta funkce definována jako součet nekonečné řady (1). Když se s proměnnou "s" blížíme k jedničce (shora), tento součet postupně roste a pro s=1 se stane nekonečným (tomuto speciálnímu případu se říká "harmonická řada"). Zeta funkce má proto v bodě s=1 tzv. jednoduchý pól (nekonečnou špicu).
Daleko zajímavějí jsou vlastnosti tohoto nekonečného součtu pro komplexní čísla z=s+it. V tomto případě se dá funkce rozšířit i do konvergenčně zapovězených oblastí. Zeta funkce je v komplexním oboru definována formálně stejným vztahem (2), jen musíme mít na paměti, že mocniny s komplexním exponentem jsou trochu zapařenější obludy (4). Tato formulka je v podstatě variací na definici obecné mocniny pomocí exponenciely. Pro kladné reálné číslo a>0 a libovolné komplexní b definujeme: a^b = exp(b*ln(a)).
Protože nekonečný součet je trochu abstraktní a pro běžného smrtelníka esoterický pojem, vypomáháme si při studiu nekonečných řad tzv. částečnými součty (3). Zafixujeme si exponent (proto už ho v rovnici (3) explicitně neuvádím) a pro každé přirozené N prostě sečteme prvních N členů řady. To už je konečný součet, takže si s ním poradí i školák, a my můžeme v klidu sledovat jak se výraz S(N) chová pro zvětšující se N - to je základem studia nekonečných řad.
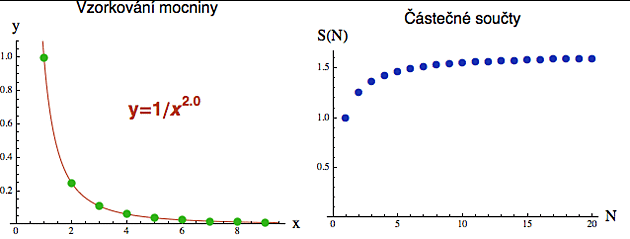
Ty členy, které sčítáme, si můžeme představit jako mocninnou funkci, vyčíslenou pouze v přirozených číslech (viz zelené bambulky vlevo). Takový obrázek nám dává celkovou představu, jak se ta sčítaná čísla chovají. V jistém smyslu jsme tu mocninu navzorkovali a takto obdrženou posloupnost pak sečetli.
Na obrázku níže jsem navzorkoval funkci 1/x2, takže prvních pár členů (zelené body) odpovídá hodnotám 1, 1/4, 1/9, 1/16, 1/25 atd.
Příslušné částečné součty jsou na obrázku vpravo. Prvních pár se dá sečíst v ruce:
S(1) = 1
S(2) = 1 + 1/4 = 5/4 = 1.25
S(3) = 1 + 1/4 + 1/9 = 49/36 = 1.36
S(4) = 1 + 1/4 + 1/9 + 1/16 = 205/144 = 1.42
Když si to naprogramujete ve smyčce, tak zjistíte, že ty částečné součty se pro zvětšující se N blíží hodnotě 1.64493..., což odpovídá známému výrazu pro celkový součet této řady: ?2/6. Mimochodem, součet nekonečné řady se definuje právě jako limita posloupnosti částečných součtů - ale to jen tak pro zasmání.
Je celkem jasné, že aby ta řada konvergovala (tj. měla konečný součet), tak se její členy musí poměrně rychle zmenšovat (jinak by ty částečné součty nekontrolovaně rostly).
Hezky je to vidět pro funkci 1/sqrt(x), která je navzorkovaná na dalším obrázku. Zelené bambulky opět reprezentují čísla, která sčítáme, ty modré pak ukazují jejich mezisoučty.
Tady se ty zelené hodnoty sice zmenšují k nule, ale příliš pomalu. Jejich nasčítáním se nakonec dostaneme k nekonečnu. Už druhý částečný součet je zde roven
S(2) = 1 + 1/sqrt(2) = 1.70711
a jak je vidět z obrázku, další částečné součty poměrně rychle rostou. Podrobnější analýzou se ukáže, že rostou nade všechny meze a součtem celé řady je nekonečno. Náleží tedy k řadám divergentním.
Mimochodem, všimněte si, že ty částečné součty se chovají zcela monotonně, tedy nijak se nevlní, nepadají z útesu, nejsou v nich patrné žádné náhlé poryvy větru atd. To je způsobeno tím, že mocnina je zafixovaná a při sčítání probíráme poctivě všechna přirozená čísla, takže není důvod, aby se ty modré body jakýmkoliv způsobem "potácely" (za chvli uvidíme, že pro komplexní exponenty se ty součty chovají podstatně "opileji").
To, zda se členy řady zmenšují dostatečně rychle se dá zjistit pomocí tzv. konvergenčních testů. To je ale poměrně technická záležitost, takže si nebudeme kazit slunné dopoledne a raději se hned přesuneme ke komplexním exponentům.
+++++++++
I zde se vyplatí na členy řady (2) pohlížet jako na vzorkování z příslušné spojité funkce. Ve formulce (4) si na chvíli představte, že proměnná n je nějaké zvětšující se kladné reálné číslo. Finální výraz vpravo má dvě součásti. Ta nehoráznost v závorce je číslo na jednotkové kružnici a výraz před závorkou nám ukazuje, zda se "kružnice" se zvětšujícím n nafukuje a nebo splaskává. Jedná se tedy de fakto o spirálu, která bude pro s>0 dostředivá a pro s<0 odstředivá (nezapomeňte, že ve vzorečku (3) jsou mocniny ve jmenovateli, takže při aplikaci (4) je nutno změnit znaménko).
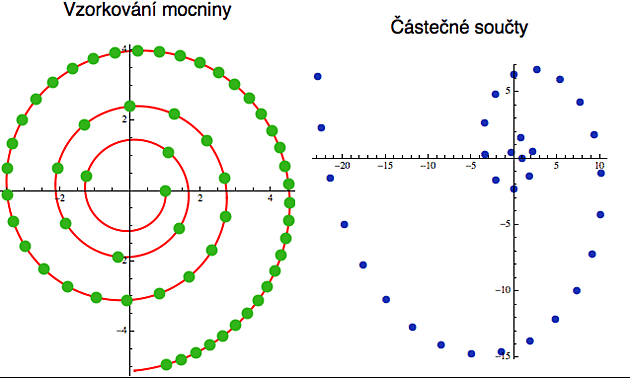
Na dalším obrázky vidíme vzorkování pro komplexní mocninu t^z s exponentem z = -0.4+5i (reálné číslo t je parametr spirály a běží od 1 do nekonečna). Tady už bohužel nemohu vynést N na osu x, protože komplexní čísla zaberou obě osy. Závislost na N je daná implicitně posloupností těch bodíků. Všimněte si, že ve finální závorce formulky (4) figuruje výraz ln(n), což v podstatě znamená, že "úhlová rychlost" se při pohybu podél spirály stále snižuje a my ji tedy (se zvyšujícím se n) vzorkujeme stále podrobněji.
Příslušné částečné součty jsou vidět na obrázku vpravo. Začneme ty zelené bodíky (které reprezentují jednotlivé členy ve formulce (2)) sčítat ve smyslu komplexních čísel a jako mezisoučty dostaneme bodíky modré. Ten první sedí v jedničce a ty další si musíme spočítat s kalkulačkou, např.
S(2) = 1 + 1/2^z = 1 + 1/2^(-0.4+5i) = -0.25+0.42i (zaokrouhleno)
Na první pohled to vypadá, že i ty částečné součty se pohybují po nějaké mocninné spirále (která je jiná, než ta původní vlevo). To zase tak velké překvapení není. Integrál mocniny je mocnina (byť jiná) a součet koneckonců není nic jiného než diskretní verze integrálu. Jen je potřeba se na to dívat asymptoticky (tedy v limitě pro velká N), protože pro součty nemáme obecně tak pohodlné formulky jako pro integrály (pokud vás to zajímá podrobněji, mrkněte se sem).
+++++++++
Teď když víme, co jsou to částečné součty S(N), podíváme se jak vypadají pro pár komplexních exponentů. V rámci následujících dvojobrázků uvidíte vlevo reálnou část S(N) vynesenou proti logaritmu N (aby bylo trochu vidět, jak se S(N) mění s N) a v pravé části pak ty částečné součty opět vynesu v komplexní rovině (abychom viděli celkový obraz).
Začnu dvěma obrázky z původního blogu. Nejprve pro případ s>1, kdy definiční řada (2) konverguje. Hodnota Zeta funkce je vyznačena červeně a vidíte, že částečné součty k ní poslušně konvergují.
Pro s<1 řada nekonverguje, ale to nám nebrání vykreslit si její částečné součty (ty se dají vytvořit nezávisle na tom, zda řada má nebo nemá konečný součet). Tady je příklad.
Vidíte, že i když řada diverguje (částečné součty se spirálovitě zvětšují a nakonec odlétnou do nekonečna), hodnotu Zeta funkce (v červeném) si můžete představit jako jakousi osu otáčení, od které se ta výsledná spirála odvíjí.
To, že ta součtová spirála je ze začátku rozdrobená do chaotické změti bodů je v podstatě způsobeno tím, že pro malé hodnoty n v rovnici (2) ty zelené bodíky nedokáží tu původní (mocninnou) spirálu dostatečně hustě navzorkovat (jak je patrné i z toho ilustračního obrázku).
Obecně tedy platí, že i v oblastech, kde už definiční vztah (2) nefunguje si stále můžeme Zeta funkci představit jako osu kolem které se ta součtová (divergující) spirála otáčí.
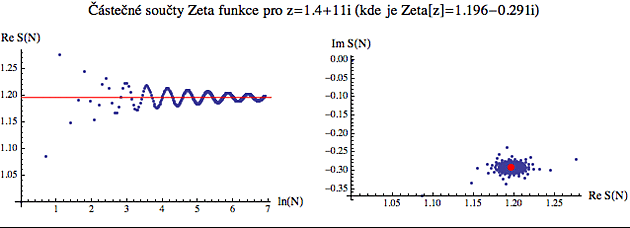
Na dalším obrázku jsem trochu zvýšil imaginární složku z a vidíte, že to počáteční "tápání" o něco zesílilo (to je proto, že imaginární složka "diriguje" rychlost otáčení, takže ty vnitřní větve spirály se zelenými bodíky jsou pak navzorkované velmi nedostatečně).
Nicméně stále platí, že nakonec si to "sedne" a částečné součty se začnou poslušně otáčet kolem hodnoty Zeta(z), opět zvýrazněné červeně.
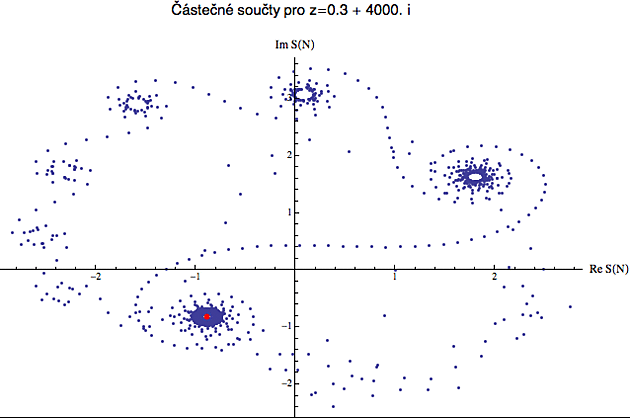
Když ovšem tu imaginární složku dále navýšíme (zde na hodnotu 950), objevíme zajímavý fenomén. V tom počátečním chaotickém poskakování se najednou začne vynořovat obláček, který trochu připomíná tu výslednou spirálu - jen se otáčí kolem jiného bodu.
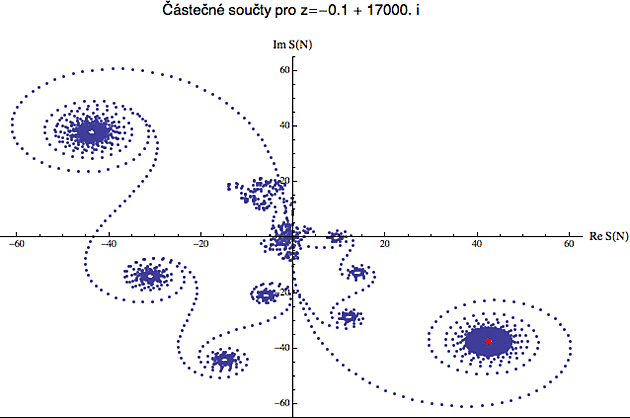
Abychom tento fenomén mohli dobře pozorovat, ještě trochu zvětším imaginární složku a místo dvojobrázku se podíváme na dva separátní obrázky.
A tady už vidíte, proč je Riemannův problém tak záludný. Ona si ta Zeta funkce (resp. její částečné součty) nejprve projde několika "falešnými" spirálami než se navine na tu pravou. Kolem těch "falešných" se sice chvíli zkusmo točí, ale nakonec odlétne jinam. A to samozřejmě analýzu Zeta funkce ztěžuje.
Také si všimněte, že na rozdíl od reálných exponentů, kde se ty částečné součty chovaly velmi ukázněně, mají ty komplexní spíše charakteristiku zbrklého puberťáka - hopsají si po komplexní rovině a co chvíli si prostě postaví hlavu a vyrazí hopsat někam úplně jinam.
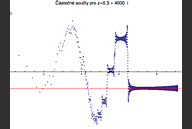
A při tom v té formulce (3) máme stále konstantní exponent a sčítáme poctivě přes všechna přirozená čísla. Na dalším obrázku je ta vrtošivost ještě patrnější (tady už náhlé poryvy větru řádí o sto šest a o pády z útesu taky není nouze).
Stojí za zdůraznění, že i přes vrtošivé chování částečných součtů, které si přelétají z jedné spirály na druhou, se ty původní zelené bodíky (které sčítáme) stále točí podél jedné a té samé samé spirály, určené exponentem z=s+it.
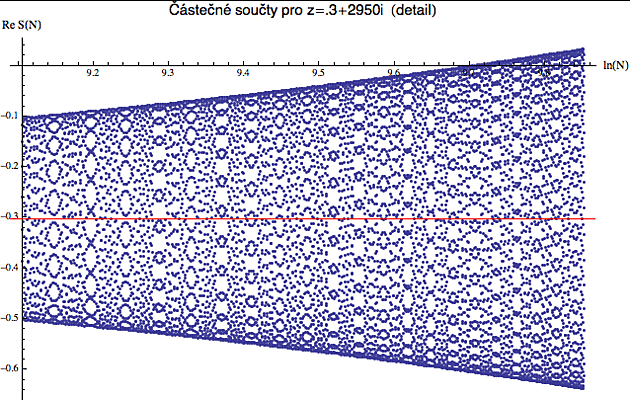
A mimochodem, ani ta poslední fáze, kdy už se to točí kolem "správné osy", není úplně nudná. Když si ji pořádně zvětšíme (a vykreslíme reálnou složku proti ln(N)) dostaneme celkem zajímavou krajku.
Její proměnlivost je opět způsobena tím, že ve formulce (4) máme v sínu a kosínu nikoliv n ale ln(n), takže otáčení se zpomaluje a to při vykreslení generuje různé vzorky - jako když si hrajete se spirographem.
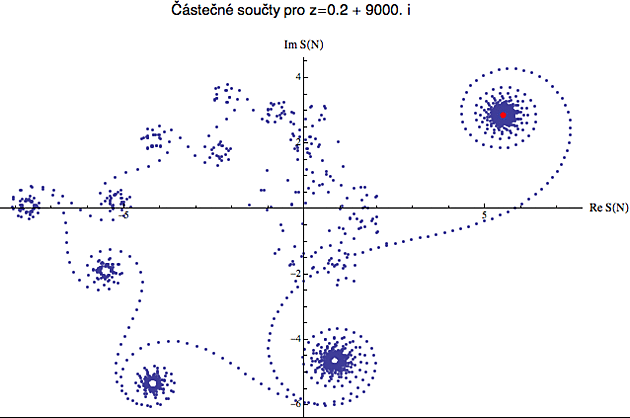
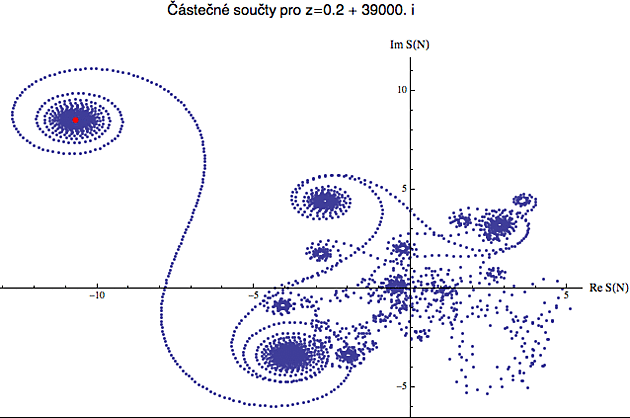
Další dva obrázky (a tentokrát už jen celkový pohled) ukazují, že pokud nadále zvyšujeme imaginární složku, počet a komplexita těch popínavých růžiček utěšeně roste.
V nadmořské výšce 99000 imaginárních jednotek už na komplexní zdi nalezneme hotovou popínavou džungli.
Pokud si myslíte, že jsem si ty růžičky vymyslel a vkreslil do grafu inkoustovou tužkou, můžete se poohlédnout po Internetu a najdete jich celou řadu (viz zde a nebo zde a nebo ve formátu pdf zde).
Určitě vám ale neuniklo, že mají všechny podobný tvar. Připomínají Eulerovu spirálu, jejíž křivost se zvyšuje úměrně s délkou křivky (více o nich naleznete v tomto pdf a nebo zde). Pro hodnoty z na kritické přímce by středy těch spirál dokonce měly být symetrické k několika prvním součtům S(N).
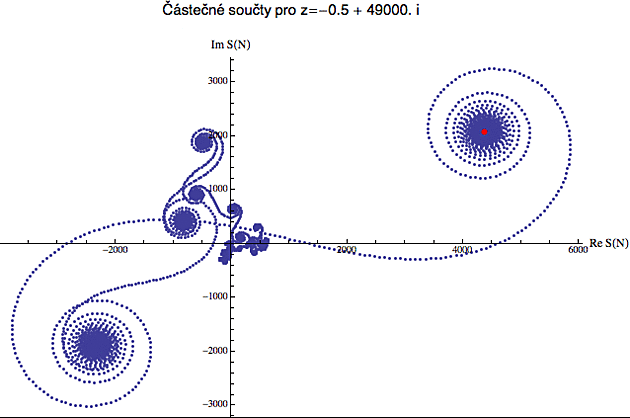
Na rozloučenou s tímto pozoruhodným světem si dáme jednu obzvlášť povedenou kreaci. Pokud si s tím budete hrát sami - a není to nic těžkého, prostě si naprogramujete součet komplexních čísel - doporučuji volit za reálnou složku z malá záporná čísla. Tam jsou ty spirálky nejhezčí.
A jaké z toho plyne poučení?
Jednak je vidět, že přirozená čísla nejsou zase tak úplně "homogenní", jak by se na první náhled mohlo zdát a komplexní Zeta funkce z nich tu "nehomogenitu" dokáže vyždímat (je to skoro jako by v přirozených číslech existovaly určité "rezonance"). A klíčem k té jejich "hrudkovitosti" je samozřejmě faktorizace.
A druhak je vidět, že i zcela jednoduchý proces (sčítání komplexních mocnin přirozených čísel) dokáže vytvořit netriviální, zdánlivě nahodilé a téměř umělecké obrazce. Nábožensky založený člověk by v nich dokonce mohl spatřit ruku Stvořitelovu. Koneckonců známý německý matematik Leopold Kronecker kdysi řekl: "Bůh stvořil celá čísla, vše ostatní je dílem člověka".
(další růžičky s anglickými popiskami najdete zde)
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
Jan Řeháček
Co rok dal

Začátek nového roku je tradičně příležitostí k ohlédnutí za rokem starým, takže jsem prohrábl archív a vylovil z něho pár fotografií z našeho parku, které si nenalezly cestu do některého z předchozích tématických blogů.
Jan Řeháček
Politické školení mužstva: Pyšná princezna

Roto končit! Pozor! (vejde útvarový politruk) Soudruzi vojáci, kapitál se potácí. Ale sám se nám na smetiště dějin nevypotácí. My mu musíme co, soudruzi? No? Nikdo? No, my mu musíme pomoci, vy hlavy hovězí!
Jan Řeháček
Ten podzim se nám hezky vybarvil

Každý podzim je v našem parku trochu jiný. Stromy, které by loni přešminkovaly i šestnáctku před prvním rande, jsou letos pobledlé jako Rusalka. A ty, které se zprvu barevně upejpaly, se najednou utrhly z řetězu. Jak řezníkův pes.
Jan Řeháček
Paroháčů je letos dost

Srnka je v našem parku jako houska na krámě. Zato setkání s jelenem si člověk musí považovat. Letos jsem ale náhodou objevil, kde se srocují: na záložním travnatém parkovišti, kterému se říká Gil's Hill, těsně před západem slunce.
Jan Řeháček
Chřadnoucí prales - pod vodou i nad ní

O korálovém útesu se říká, že je to "dešťový prales" oceánu. Biodiversita, kterou reprezentuje je ohromující. Totéž platí i o jeho suchozemském ekvivalentu. Bohužel, oba ekologické systémy se dostávají na seznam ohrožených druhů.
Jan Řeháček
Letní kvítí

Primární sezónou květů je sice jaro, ale ani léto není v našem parku z pohledu barev úplná nuda. Tady je malá fotovonička složená z příspěvků místní flory. Aneb kdo nekvete s námi, kvete proti nám.
Jan Řeháček
Plody léta

Léto je časem zrání a ani v našem parku tomu není jinak. Zajímavé plody nabízí říše rostlinná i živočišná. Tady je malý průřez letošní nabídkou: asijské maliny, kuriózní houby a malí mývalové. Ceny jsou mírné: léto létá zdarma.
Jan Řeháček
Kvetoucí fuga (Beethoven)

V Beethovenově Misse Solemnis nalezneme spoustu skrytých drahokamů, které zde leží prakticky nepovšimnuty, protože celková hudební struktura této Mše je na první poslech naprosto neprůstřelná. Jedním z nich je fuga v závěru Creda.
Jan Řeháček
Sovy a supi

V našem parku také poletuje spousta zajímavých ptáků. Tak jsem jich pár vyfotil. Sovy jsou sice nočními živočichy, ale na jaře se občas dají zastihnout i za denního světla. A za pár šupů k nim přihodím ještě pár supů. Ať nežeru.
Jan Řeháček
Vlčí západy

Při procházkách naším parkem občas fotím západy slunce z vyvýšeného travnatého parkoviště zvaného Gil's Hill. Říkám jim Vlčí západy. Jednak proto, že mají zhusta barvu vlčích máků a jednak proto, že náš park se jmenuje Vlčí past.
Jan Řeháček
Za devatero fotkami: Malebné peklo

Já to tušil, že jednou skončím v pekle. Jen jsem si představoval, že vstup bude mít z nějaké islandské sopky. Houbeles! Jeho vchod se nalézá poblíž vesničky Medkovy Kopce nedaleko Hlinska. "Lasciate ogne speranza, voi ch'intrate".
Jan Řeháček
Sedm divů jara

Po dlouhém barevném půstu zimní šedi působí návrat jarní kavalerie jako zjevení. V našem parku v tomto období kvete několik dřevin, s jejichž uměleckými kreacemi bych vás v tomto blogu rád seznámil. Matička příroda dokáže kouzlit.
Jan Řeháček
strž

V dnešním pokračování poetického cyklu "Bez básně a Hany" se nedozvíme jakou krevní skupinu mají nejraději novozélandští upíři a zda je tuna pampeliškového chmýří těžší než sbírka maturitních příkladů z matematiky.
Jan Řeháček
Devět zastavení času

Příroda se mění pomalu, ale jistě. Den ze dne nic nepostřehnete, ale když se na známá místa vrátíte za pár týdnů, naleznete desítky drobných změn. Tak jsem se na třech místech našeho parku devětkrát zastavil, abych je zachytil.
Jan Řeháček
Cesta do hlubin duše (Beethoven)

Lidská duše je odvěkou hádankou, na které si vylámaly zuby celé generace psychologů, teologů a filosofů. Tajuplný komplex uvnitř každého z nás. Pro mne je definicí lidské duše Beethovenův 14. smyčcový kvartet cis moll, op. 131.
| předchozí | 1 2 3 4 5 6 7 ... | další |
- Počet článků 402
- Celková karma 19,53
- Průměrná čtenost 920x