Matykání: Jára di Mensa - algebraik samouk
Jára di Mensa (vlastním jménem Guadalajara Uomodellastanza) se narodil v roce 1863 do rodiny chudého milánského multimilionáře. Již jako pětiletý dosáhl IQ 189 (byť s nedovolenou podporou větru) a stal se řádným členem milánské pobočky Mensy. Hned o rok později ho jeho ambiciózní otec nechal zapsat na prestižní lyceum s rozšířenou výukou matematiky, aby donosil úhloměr po své starší sestře Luise.
Jako osmiletý objevil nezávisle Pythagorovu větu a byl neskonale zklamán, když mu úředník na patentovém úřadu poťouchle oznámil, že přichází o pouhých 2371 let později. Malý génius ale nezahořkl a v roce 1878 navzdory všem posměváčkům revolucionizoval výuku matematiky vynálezem parního kružítka. Mělo na svou dobu téměř ekologickou spotřebu - půl kila uhlí na kružnici.
Současně se věnoval pedagogické teorii a rozpracoval tezi, podle níž by se všichni slavní objevitelé měli okamžitě po svém objevu přejmenovat tak, aby se jejich jméno žactvu lépe pamatovalo. Například indický matematik Srinivasa Ramanujan by se podle něho v učebnicích lépe vyjímal jako Rambo. Jeho návrh se nakonec dočkal částečné implementace a profesor fyziky na berlínské univerzitě, Maxmillian Wolfeschlegelhausenberger, na jeho doporučení vešel do historie jako Max Planck.
Mistr sám šel příkladem a po objevu logaritmu se základem 9387, který do té doby nebyl v matematické literatuře popsán, přijal podstatně kratší jméno Jára di Mensa. Pod tímto pseudonymem publikoval svou první monografii "O původu kvantit", ve které všechny veličiny rozdělil na ty, o kterých se zasvěceně diskutovalo ve foyeur milánské opery (těm říkal scaláry) a na ty, o kterých se bez obalu mluvilo na italském venkově (těm říkal traktory). Scaláry tedy byly jakési "lepšoveličiny", zatímco traktory se aplikovaly spíše na poli polí.
Bohužel vlivem nejistého rukopisu odborného recenzenta po 14 skleničkách Brunello di Montalcino bylo slovo "traktory" nesprávně interpretováno jako "vektory" a moderní dělení veličin spatřilo (mlhavé) světlo světa. Omylem. Naprostá bezobsažnost tohoto matematického termínu vystupuje nejostřeji právě v souvislosti se silovým polem (ve starších učebnicích "silážním"). Zatímco pojem "traktorové pole" je znám každému, kdo někdy viděl podzimní orbu, spojení "vektorové pole" bylo dlouhou dobu pouze "předmětem vášnivých debat v anarchistických kroužcích" - jak by řekl již zmíněný Jára Cimrman.
V roce 1889 prováděl di Mensa delikátní měření tělesných proporcí manželky milánského špagetáře Luigi Piccipucciniho. Aby v případě náhlého návratu pana chotě nedošlo k nechtěnému provalu "indiscrezione", připravil si úkrytový prostor za dveřmi ložnice - samozřejmě po odborném ověření, že jeho vlastní výška i šířka je menší než příslušné rozměry dveří. Bohužel v reálném provedení zapomněl na třetí rozměr a jeho pupek ne a ne se vtěsnat za dveře. Di Mensu tato tragická událost podnítila k samostudiu lineární algebry a ledva zmizel otok na jeho levém oku, odložil vidličku s nenáviděnými špagetami a počal sepisovat rozdíly mezi plošnými a prostorovými objekty. Jeho geometrické bádání vyústilo ve zcela fundamentální objev, který nese dodnes jeho jméno.
V latině se mu říká "dimensa", v angličtině "dimension" a v češtině "dimenze".
+++++++++
Dimenze
Minule jsme si řekli něco málo o nezávislých vektorech, takže nebudu dělat žádné drahoty a rovnou to na vás vybalím.
Dimenze vektorového prostoru je v podstatě maximální počet lineárně nezávislých vektorů, které se z něho dají vybrat.
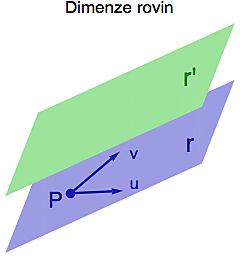
Je to tedy určitý typ kapacitní veličiny a ukazuje, že v daném vektorovém prostoru si nelze zvolit libovolně velkou množinu nezávislých vektorů (směrů). Dimenze je strop takového počínání. Například v rovině lehce nalezneme dva nezávislé vektory u a v (kterékoliv nekolineární). Když se ale budeme pokoušet najít třetí vektor w, tak aby trojice (u,v,w) byla lineárně nezávislá, zjistíme, že už to nejde. Do roviny se více než dva nezávislé směry nevejdou a má tedy dimenzi 2. V prostoru bychom ještě jeden nezávislý směr nalezli - například tak, že bychom si vzali kolmici na rovinu r určenou vektory u a v. Ale víc ani ťuk. Proto má prostor dimenzi 3.
Minule jsme se na nezávislost vektorů podívali algebraicky. Protože v definici dimenze hraje nezávislost kruciální roli, podívejme se na pár lineárních kombinací ještě geometricky.
Představme si, že v rovině máme traktor, které umí jezdit pouze dvěma směry - modrým a zeleným (místo volantu má tedy dva čudlíky pro výběr směru). Kdo chce zůstat ve světě vektorů, může si každý směr představit jako množinu všech násobků nějakého pevného (třeba jednotkového) vektoru - na obrázku vlevo jsou vyznačeny černě.
Přestože to tak na první pohled nevypadá, tak s tímto primitivním traktorem se v rovině dostaneme do kteréhokoliv bodu, např. tomu, který odpovídá polohovému vektoru z (červeně) nebo z' (oranžově). Stačí spustit naznačené rovnoběžky s osami, popojet kousek v jednom směru, pak "přepnout" do druhého a jsme na místě.
Kruciální předpoklad je, že ty dva směry u a v jsou nezávislé. Pokud by splynuly (tj. vektory tyto směry reprezentující by byly kolineární), pak bychom mohli "přepínat" jak mourovatý, ale nikam mimo "splynutou přímku" bychom se nedostali. Jakmile ty směrové nůžky rozevřete, celá rovina je vaše. A v tom je jádro lineárního pudla.
Řečeno jazykem lineární algebry: jakýkoliv třetí vektor z dostaneme vhodným zkombinováním vektorů v modrém a zeleném směru, což algebraicky znamená
(P0) z = a*u + b*v, pro vhodné konstanty a, b.
(přidání dalšího vektoru z k dvojici nezávislých už tedy nutně vytvoří lineární závislost, explicitně vyjádřenou v předešlé rovnici)
V prostoru by to bylo jiné (pravá část obrázku). Zde ten třetí nezávislý vektor w najdeme, jen ho musíme "zvednout" z roviny r (určené předchozími vektory u a v). Pak už ho žádná kombinace vektorů u a v nevygeneruje (traktor jezdící pouze v těchto směrech se "do vzduchu" nevznese - je omezen na modrou rovinu r). Do prostoru se tedy tři nezávislé vektory napěchovat dají (zde u, v a mimo rovinu trčící w). Čtyři už ne - jakýkoliv další prostorový vektor z už by byl dosažitelný 3D traktulníkem (kombinace traktoru a vrtulníku) schopným pohybu ve směrech u, v a w. Itinerář takové cesty se nejlépe čte pozpátku - ze špičky vektoru z byste se nejprve podél směru w vrátili po tečkované trase zpátky do původní roviny (bod Q) a v ní už byste se kombinací směrů u a v dostali do počátku jako v předchozím případě. Čtveřice u, v, w a z by tedy byla lineárně závislá (protože vektor z je kombinací u, v a w).
+++++++++
Tato geometrická intuice (spojená s rovnoběžným promítáním) vám pouze naznačí, že ta či ona kombinace existuje. Pokud byste její konstanty chtěli získat explicitně, musíte se opět (jako jsme to udělali minule) uchýlit k algebraickému výpočtu. Aneb jak říkával sám Jára di Mensa: "co si nespočítám sám, jiný za mě nespočítá" (za domácí cvičení si můžete vygooglovat, kdo ho k tomuto výroku inspiroval).
Příklad: zvolme si pro jednoduchost u = (1,0) a v = (1,2) a budeme chtít vědět, jaké přesné násobky těchto vektorů musíme vzít, abychom dojeli do bodu, odpovídajícího (polohovému) vektoru z = (3,2). K tomu stačí si rozepsat výše citovanou abstraktní rovnici (P0) pro dvě neznámé konstanty do souřadnic:
3 = 1a + 1b (porovnání prvních souřadnic)
2 = 0a + 2b (porovnání druhých)
Řešení bude a=2 a b=1. Musíme tedy ujet dvojnásobek vektoru u v modrém směru a jednonásobek vektoru v v zeleném. Tady je ten výpočet celkem snadný, ale čím více vektorů a souřadnic, tím více rovnic, takže hledání kombinací pak vyžaduje pokročilejší metody.
+++++++++
Dimenze je tedy veličina, která nám naznačuje "velikost" vektorového prostoru.
V matematice existuje spousta způsobů jak měřit velikost nějaké množiny - od prostého spočítání jejích prvků (tomu se říká mohutnost množiny) až po vyčíslení jejího obsahu či objemu (tomu se říká míra množiny). Tyto se ale pro vektorové prostory příliš nehodí. Přímka, rovina, prostor i vícedimenzionální ekvivalenty obsahují nekonečně mnoho bodů, a ani míra nám neumožní dostatečné rozlišení, protože přímka má nekonečnou délku, rovina nekonečný obsah a prostor nekonečný objem.
Dimenze je naproti tomu šitá vektorovým prostorům na míru, protože se opírá o centrální pojem lineární kombinace vektorů (ze kterého se pak dovozuje nezávislost). Přímka má tedy dimenzi 1, rovina dimenzi 2 a prostor dimenzi 3, protože se do nich "vejde" stále víc a víc nezávislých vektorů.
Zhruba řečeno: dimenze nám ukazuje kolika nezávislými směry se v daném vektorovém prostoru můžeme vydat.
Mimochodem, analýzou pohybu traktoru či traktulníku jsme zjistili zajímavou věc. V okamžiku kdy máte k disposici ten maximální počet nezávislých vektorů, tak si z nich můžete nabrnkat každý vektor. Na tomto postřehu je založena alternativní definice dimenze.
+++++++++
Báze
Vektorů je - abych to řekl nějak exaktně - strašně moc.
Jen v rovině máte na výběr nekonečně mnoho směrů a v každém si můžete vybrat vektor libovolné délky. Proto se naskýtá přirozená otázka, zda bychom nenašli nějakou základní (a pokud možno co nejmenší) množinu vektorů, ze které by se všechny ostatní daly nabrnkat pomocí lineárních kombinací.
Je to něco podobného jako hledání prvočísel, ze kterých se všechna ostatní čísla dají nabrnkat pomocí součinu. Lidstvo neustále hledá nějaké atomy, ze kterých se vše ostatní dá "nabrnkat".
Ukázalo se, že v "rozumných" vektorových prostorech se taková množina dá najít poměrně snadno - v předchozí sekci jsme ji nalezli takřka mimoděk (vektory u a v) - a říká se jí báze. Je to nejmenší množina vektorů, ze které se dá celý vektorový prostor kompletně zrekonstruovat (to slůvko nejmenší je tu nutné, protože kdykoliv si dokážete vektor zkombinovat ze dvou jiných, např. w=2r-3s, tak si ho dokážete zkombinovat i ze tří w = 2r-3s+0t; byla by tu tedy malá nejednoznačnost).
Kterékoliv dva nezávislé vektory u a v tvoří bázi roviny, protože (jak jsme viděli) každý vektor z se pak dá napsat (a v tomto případě jednoznačně) jako jejich kombinace. Báze sama o sobě ovšem jednoznačně určena není (na rozdíl třeba od prvočísel). Můžete si zkusit ty dva vektory u a v pootočit o libovolný úhel a stále to bude báze (i z těch pootočených vektorů si nabrnkáme cokoliv), takže v tomto případě je bází dokonce nekonečně mnoho.
Pro některé báze je výpočet kombinací snazší než pro jiné. Např. pro e1=(1,0) a e2=(0,1) se neznámé koeficienty v příslušných rovnicích krásně odseparují a rozklad vektoru z=(2,3) na kombinaci e1 a e2 pak zvládne i malé děcko.
z = 2 e1 + 3 e2 = 2 (1,0) + 3 (0,1) = (2,3)
(této bázi se říká kanonická a představuje asi nejlepší způsob, jak nahlédnout, že standardní Eukleidovský prostor R^n má dimenzi n - vektory báze ei leží v souřadných osách, tj. mají 1 pouze na i-té pozici, jinak 0, a jak se z nich rekonstruují všechny ostatní vektory je nabíledni)
A nebo studenty potrápíme a necháme je spočítat rozklad vektoru w=(2,3) pro bázi r=(3,8) a s=(2,5), Tady už to od oka netrefíte a musíte to opět spočítat rozkladem do souřadnic. Vyjde vám:
w=-4r + 7s
+++++++++
Zda nějaká množina vektorů tvoří bázi, popřípadě zda se dá na bázi doplnit je poměrně komplikovaná otázka, na kterou má lineární algebra spoustu chytrých vět, ale v jednoduchých příkladech se můžete spolehnout na selský rozum. Na přímce si všechny vektory nabrnkáte z jednoho (bázového), v rovině ze dvou, v prostoru ze tří atd. A jsme zpátky u dimenze.
Pokud se vám pojem báze zdá stravitelnější než nezávislost vektorů, můžete si dimenzi představit jako počet prvků báze - a tak se taky ve skriptech velmi často definuje - tedy minimální počet vektorů, ze kterých se dá celý vektorový prostor zrekonstruovat.
To vypadá na první pohled jako paradox - protože dimenze je přece maximální počet nezávislých vektorů, které se do toho prostoru dají nacpat. Ale když si to rozmyslíte (a není to úplně triviální), zjistíte, že každá maximální množina nezávislých vektorů je současně nejmenší množina, ze které se ten prostor dá "nabrnkat" (tj. báze) a naopak.
Zhruba řečeno je to proto, že v okamžiku, kdy získáte tu maximální množinu nezávislých vektorů, říkejme jí M, tak z nich už si vše ostatní vygenerujete (protože přidáním libovolného nenulového vektoru w k M dostaneme množinu závislou a tudíž najdeme netriviální kombinaci, která vyjádří w pomocí vektorů z M). A že je to minimální množina s touto vlastností je vidět z toho, že když jeden z těch nezávislých vektorů množiny M vyhodíte, tak už nebude pravda, že ta ochuzená množina zrekonstruuje celý prostor. Ten vyhozený vektor se z ní nakombinovat nedá (kdyby se dal, tak by ta množina M nebyla nezávislá, jelikož jeden z jejích vektorů by se dal zkombinovat z těch ostatních).
V mnoha učebnicích se báze definuje jako množina vektorů, ze které se dá každý vektor vyjádřit jednoznačně, čímž se ta minimalita "rekonstrukční množiny" elegantně obejde (ona se z té jednoznačnosti dá odvodit). Studenti si pak s tímto zdánlivým paradoxem nemusí lámat hlavu.
Příklady bází a nebází pro vektorový prostor V=R2:
u=(1,1), v=(1,-1) ... (báze: po kanonické asi nejpoužívanější)
u=(1,2), v=(1,3) ... (báze: vektory nemusí být kolmé)
u=(1,1), v=(-3,-3) ... (nebáze: z vektorů se nedá zrekonstruovat V, jsou kolineární)
u=(1,1), v=(1,2), w=(1,3) ... (nebáze: není to minimální "rekonstrukční" množina)
(z těch posledních vektorů se V sice zrekonstruovat dá, ale kterýkoliv z nich můžeme vyhodit a rekonstrukce bude stále možná)
+++++++++
A k čemu je taková báze dobrá?
Její vektory - stejně jako ta prvočísla - fungují jako elementární částečky dané algebraické struktury, ze kterých se vše ostatní dá složit kombinací.
Hezky je to vidět u funkcí, které respektují příslušné algebraické operace.
Pro spoustu celočíselných funkcí (které respektují součin, tj. jsou multiplikativní) stačí znát chování v prvočíslech a hodnoty funkce ve složených číslech se z nich pak dají odvodit.
Bázové vektory poskytují podobnou službu.
Funkce (z jednoho vektorového prostoru do druhého), které respektují vektorové operace se zovou lineární. Jako takové musí splňovat dvě podmínky
P1: f(u+v) = f(u)+f(v), pro každé vektory u a v
P2: f(cu) = c*f(u), pro každý vektor u a každý skalár c
(tyto podmínky vlastně říkají, že funkce f je v jistém smyslu skamaráděná s oběma operacemi, které jsou na vektorovém prostoru definovány - a jsou to podmínky poměrně silné, proto mají lineární funkce spoustu žádoucích vlastností, které nelineární funkce nemají)
Takovou funkci si opět nejlépe představme jako skříňku s trpaslíkem, kam vhodíme vstupní vektor u, trpaslík s ním něco vyvede a na výstupu nám vyhodí vektor v=f(u). Pokud je výstupní vektor jednorozměrný, a je to tedy de facto číslo (skalár), pak takové funkci říkáme funkcionál na prostoru V.
Obecný vektor w si nyní rozepíšeme pomocí báze u1, u2, ... un
w = c1 u1 + c2 u2 + ... + cn un
(kde cn jsou příslušné jednoznačně určené koeficienty)
a lehce zjistíme, že funkční hodnota libovolné lineární funkce na vektoru w je určena hodnotami této funkce na bázových vektorech (tj. jakmile ty hodnoty známe, dokážeme spočítat f(w) pro každý vektor w)
f(w) = f(c1 u1 + c2 u2 + ... + cn un) = c1 f(u1) + c2 f(u2) + ... cn f(un)
(hodnoty cn dostaneme z vektoru w algebraicky - viz výše)
Toto není v žádném případě pravda pro funkce se kterými se člověk setká na střední škole (sin, log, exp, tan atd). Ty lineární nejsou a na vyšetření jejich chování je třeba znát podstatně víc, než jen hodnoty pro n vhodně vybraných čísel.
Ještě malé varování: na střední škole se často slovem lineární funkce označují funkce tvaru y = kx+q. Ty jsou ale lineární ve smyslu předešlé definice pouze pro q=0 (tj. přímky procházející počátkem). Jakou linearitu má autor na mysli se většinou pozná z kontextu.
Na procvičení si můžete rozmyslet, že funkce z R2 do R2 zadané formulkou
f(x,y) = (x-2y,x+y) a f(x,y) = (0,x-y)
splňují podmínky (P1) a (P2) a jsou tedy lineární, zatímco
f(x,y) = (x-y2, x*y) a f(x,y) = (1,x-y)
je nesplňují a proto nejsou lineární.
Další užitek, který báze poskytuje, si zaslouží zvláštní sekci.
+++++++++
Souřadnice
Toho, že se každý vektor dá jednoznačně vyjádřit jako lineární kombinace bázových vektorů, lze využít pro zavedení alternativních souřadnic. Pokud vektor w vzhledem k bázi u1, u2,... un můžeme zapsat jako kombinaci
w = c1 u1 + c2 u2 + ... cn un
pak n-tici čísel [c1,c2,...,cn] nazýváme souřadnice vektoru w vzhledem k dané bázi.
V minulé sekci jsme viděli, že pro bázi r=(3,8) a s=(2,5) se vektor w=(2,3) dá rozepsat jako
w = -4r + 7s
a to znamená, že vzhledem k této bázi bude mít souřadnice w=[-4,7].
To je na první pohled trochu matoucí. Vektor (2,3) se najednou "jmenuje" [-4,7]. Můžeme se zle zamračit, můžeme odložit nenáviděné logaritmické pravítko, ale to je asi tak všechno co s tím můžeme dělat - souřadnice vektoru jsou vždy vztaženy k nějaké bázi (a změníme-li bázi, změní se i souřadnice). I ty původní (2,3) jsou vlastně koeficientíky z kombinace pomocí kanonické báze
w = 2 e1 + 3 e2 = 2 (1,0) + 3 (0,1) = (2,3)
Je to podobné jako zápis celých čísel v různých systémech. Jako kanonický základ používáme samozřejmě 10 (dekadický systém), ale když na to přijde, můžeme například číslo 19 napsat v trojkové soustavě jako "201" (takže se milé číslo najednou "jmenuje" úplně jinak). Ta 19 na kterou jsme zvyklí není nic jiného než rozvoj vzhledem ke "kanonické" desítkové soustavě 19 = 1*10+9*1, zatímco trojkový zápis odpovídá rozvoji 19 = 2*32+0*3+1*1.
A s vektory je to jakbysmet. Není-li řečeno jinak, předpokládá se, že souřadnice vektoru jsou udané vzhledem ke kanonické bázi. Občas se ale stane, že pro konkretní problém je výhodnější nějaká jiná báze (např. proto, že její vektory jsou lépe "sladěné" s veličinami problému) a pak raději počítáme se souřadnicemi vzhledem k ní. Jen se musí dávat pozor na notaci. Souřadnice vzhledem k nějaké nekanonické bázi B se obvykle označují subskriptem B.
Aby se při přechodu od jedné báze k druhé nemuselo počítat moc rovnic, používají se pro přepočet tzv. transformační matice.
+++++++++
To počítání souřadnic z lineárních kombinací ale není příliš zábavné.
Naštěstí máme-li ortonormální bázi (vektory jsou navzájem kolmé a mají jednotkovou délku), můžeme si namísto algebraického výpočtu vypomoci s geometrií. Jak vidíme na obrázku vpravo, souřadnice vzhledem k bázi B (z vektorů u a v) se dají spočítat pravoúhlým průmětem vektoru w do bázových vektorů u a v a to je pouhé dosazení do vzorečku (v minulé sekci Jauvajs je příklad).
Obecně platí, že pro ortonormální bázi u1, u2, ... un se vektor w vyjádří takto:
w = (w,u1) u1 + (w,un) un + ... + (w,un) un
a souřadnice jsou pak skalární součiny s bázovými vektory
ci = (w,ui)
I proto se vyplatí bázové vektory ortonormalizovat (asi nejznámějším algoritmem k tomuto účelu je Gramova-Schmidtova ortogonalizace).
+++++++++
Jednou z důležitých vlastností vektorových prostorů je, že všechny možné báze mají stejný počet prvků (to nám umožnilo alternativní definici dimenze). To znamená, že počet souřadnic, které dostaneme při přechodu k jiné bázi se nezmění. Na dimenzi se proto také můžeme dívat jako na minimální počet souřadnic, které potřebujeme k určení své polohy.
Slůvko "minimální" je zde opět důležité. V třírozměrném prostoru V=R3 si představme rovinu r procházející počátkem P a určenou dvěma nezávislými vektory u a v (viz obrázek vpravo). Každý bod roviny má tři souřadnice (x,y,z), "zděděné" z okolního prostoru a mohlo by se zdát, že rovina je tedy 3D objekt. Pro ni ale můžeme vymyslet "úspornější" souřadnice. Rovina r procházející počátkem je sama o sobě vektorovým prostorem a každý její bod (polohový vektor w) se proto dá napsat jako kombinace u a v:
w = au + bv
takže místo souřadnic (x,y,z) "vypůjčených" z okolního prostoru můžeme tuto rovinu popsat souřadnicemi [a,b], vzhledem k bázi u,v. I prostorová rovina je tedy dvou-dimenzionální.
Podobně bychom mohli dovodit, že i posunutá zelená rovina r' je pouze dvourozměrná (přestože tato rovina neprochází počátkem a není to tedy technicky vzato vektorový prostor). Můžeme ji ale do počátku "šoupnout" vhodnou translací, tam "změříme" její dimenzi, což bude 2, a pak ji zase nenápadně šoupneme zpátky do původní polohy. Tímto způsobem získáme informaci o dimenzi "šoupnutých" objektů, jako jsou přímky, roviny a nadroviny neprocházející počátkem (technicky vzato, "šoupnuté" objekty nejsou vektorové, ale afinní prostory).
Ta heuristika s minimálním počtem souřadnic se dá použít i pro komplikovanější (zakřivené) objekty. Např. sféru (tedy povrch koule) můžeme opatřit dvojicí souřadnic (zeměpisná šířka a délka) a opět zjistíme, že i sféra je dvourozměrná (přestože žije ve 3D prostoru). Proto se taky v matematice obvykle značí symbolem S2. Pokud si zafixujete délku, dostanete jistý poledník, a ten bude sám o sobě jednorozměrný. To je vidět jednak z toho, že se podél něho můžete pohybovat pouze v jednom směru (severojižním) a jednak z toho, že k určení své polohy podél poledníku potřebujete už jen jednu další souřadnici - zeměpisnou šířku.
Tady už jsme ale na tenkém ledě. Ani sféra ani její poledníky (v podstatě kružnice) se nedají vytvořit z vektorového prostoru pouhým "šoupnutím". Tady se budeme nejprve muset naučit vektorové prostory "ohýbat". Ale na to se podíváme až příště. Uvidíme, že dimenze má kromě trvalého bydliště ve vektorových prostorech také několik přechodných.
+++++++++
Sekce jauvajs: kovariantní versus kontravariantní
jen pro mimořádně otrlé povahy
V minulé sekci jsme viděli, že si můžeme ušetřit spoustu otravného počítání lineárních rovnic, když souřadnice nějakého vektoru w (vzhledem k bázi B) spočítáme geometricky, tj. spuštěním kolmic na souřadné osy. To funguje dobře máme-li ortonormální bázi. Pro báze jejichž vektory nejsou nutně pravoúhlé vznikne problém. V takovém případě nám ten algebraický (vpravo) a geometrický (vlevo) přístup dá rozdílný typ souřadnic [a,b].
Vpravo jsme v podstatě udělali rovnoběžnou projekci do souřadných os, zatímco vlevo projekci pravoúhlou. Přesto můžeme obě projekce použít pro získání dvou čísel (průsečíků a,b), kterými lze vektor w plně charakterizovat. Dva různé vektory budou (v obou případech) odpovídat dvěma různým dvojicím (a,b) a naopak - pokud vám na těch dvou osách zadám dva body (a,b), tak z nich ten vektor w jednoznačně zrekonstruujeme. Jinými slovy, oba přístupy múžeme použít jako generátor souřadnic. Těm vlevo se říká kovariantní a těm vpravo kontravariantní (na wikipedii najdete velmi hezkou animaci).
Pro většinu lidí by tato hrubá představa měla stačit.
Věc má ale pod povrchem jeden malý háček.
Zatímco ty kontravariantní souřadnice (vpravo) fungují tak jak očekáváme, tedy ukazují nám jak musíme zkombinovat násobky bázových vektorů, abychom dostali hledaný vektor w, vlevo to evidentně nefunguje. Když ty komponenty složíme (sečteme), dostaneme se daleko mimo vektor w. To neodpovídá představě, že souřadnice nějakého vektoru jsou prostě koeficientíky jeho rozkladu do bázových vektorů.
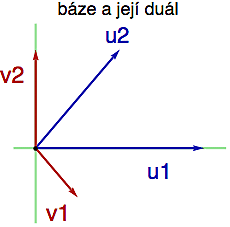
Je to tak proto, že ty kovariantní souřadnice mají své vlastní - trochu pozměněné - bázové vektory B', kterým se říká duální báze (vzhledem k bázi B). A ty kovariantní souřadnice nám neukazují jak daný vektor w složit z původní báze B, ale jak ho složit z báze duální B'. Obrazně řečeno, pokud budeme bázi B považovat za jakousi vládu vektorového prostoru, která určuje vlastnosti všech zobrazení, tak na B' se můžeme dívat jako na "stínovou vládu", která obvykle machinuje v lineárních kuloárech (zájemcům o podrobnější výklad doporučuji monografii Járy di Mensy "Puč ve vektorovém prostoru aneb s Pičipučinim na věčné časy a nikdy jinak").
+++++++++
Pro danou bázi u1,u2,...,un je duální báze v1,v2,...vn definována vztahy
(P3) ui.vj=0 (pokud je i?j) a ui.vj=1 (pokud je i=j)
Ve dvou rozměrném případě tedy pro zafixovanou bázi u1 a u2 dostaneme 4 rovnice pro 2x2 souřadnice neznámých vektorů v1 a v2 (tvořících duální bázi B').
(P3') u1.v1=1, u1.v2=0, u2.v1=0, u2.v2=1
Spočítáme si malý příklad.
V R2 si vybereme bázi u1 = (2,0) a u2=(1,1)
(kulaté závorky používám pro kanonické souřadnice)
Tyto vektory nejsou ani jednotkové, ani vzájemně kolmé (viz obrázek), ale jsou nezávislé a tudíž tvoří bázi R2 (stejný argument jako nahoře s traktorem).
Např. vektor w = (3,1) si vyjádříme pomocí těchto vektorů následovně:
w=1*u1 + 1*u2
a to znamená, že (kontravariantní) souřadnice vektoru w vzhledem k této bázi jsou [1,1]. A teď duál.
Skalární součiny prvního duálního vektoru v1 musí splňovat (viz P3')
u1.v1=1 a u2.v1 = 0
Označíme-li si jeho (kanonické) souřadnice v1 = (x,y), dostaneme pro ně rovnice
2x = 1 a x+y = 0 (vektory u1 a u2 jsou známy)
a jejich řešení nám dá v1=(1/2,-1/2). Obdobně získáme v2=(0,1).
Když si teď napíšeme, jak vyjádřit vektor w=(3,1) v duální bázi, dostaneme
w = a1*v1 + a2*v2
a rozepsáním "po složkách" spočítáme koeficienty a1 a a2:
w = 6*v1 + 4*v2
Tj. (kovariantní) souřadnice w (vzhledem k duální bázi B') jsou [[6,4]].
Všimněte si, že ty kovariantní souřadnice jsme mohli získat pomocí skalárního součinu vektoru w s původními bázovými vektory u1 a u2
w.u1 = {3,1}.{2,0}=6
w.u2 = {3,1}.{1,1}=4
zatímco kontravariantní souřadnice se dají spočítat součinem s duální bází:
w.v1 = {3,1}.{1/2,-1/2}=1
w.v2 = {3,1}.{0,1}=1
(pokud je báze ortonormální, báze B a B' splynou)
Trochu obecnější příklad naleznete v tomto pdf (sekce 16.2).
+++++++++
Ale ani tohle ještě není úplná pravda.
Ty duální vektory ve skutečnosti žijí ve svém vlastním (duálním) vektorovém prostoru, který se značí hvězdičkou V* a skládá se z funkcionálů na prostoru V (i funkcionály se dají sčítat a násobit skaláry, takže tvoří vektorový prostor). Protože každý funkcionál je lineární funkce (ve smyslu podmínek P1 a P2 výše), do které vhodíte vektor z prostoru V a vypadne vám číslo, tyto mystické objekty v jistém smyslu suplují skalární součin - zejména tam, kde jej nelze dobře definovat.
(kromě výrazu "duální vektor" nebo "funkcionál" se též používá "kovektor" či "lineární forma" - to je názvů, co? ...a při tom je to taková blbost...).
Pokud prostor V skalární součin má, tak se ty funkcionály (duální vektory) dají představit jako běžné vektory - což se pro pochopení téhle duální habaďúry docela hodí.
Nejjednodušší je to v jedné dimenzi (tj. na reálné ose R). Na obrázku vpravo vidíte lineární funkce na reálné ose - přímky procházející počátkem P (mají rovnici y=kx). Protože každá je charakterizovaná svou směrnicí k, je jich přesně tolik, co reálných čísel (1D vektorů). Každému číslu k můžeme vzájemně jednoznačně přiřadit jednu lineární funkci f(x)=kx a naopak: z každé lineární funkce můžeme vyždímat reálné číslo, její směrnici. V pravé části obrázku tedy de facto vidíme (neúplný) seznam 1D vektorů, zatímco v levé jsou zobrazeny příslušné funkcionály. Tady je ta dualita vektorů a kovektorů jako na dlani.
V n-rozměrném prostoru R^n postupujeme obdobně - každému vektoru v přiřadíme následující funkcionál F
F(u) = v.u, pro každé u z našeho vektorového prostoru.
To, že to funguje i obráceně, tj. každý funkcionál F lze takto vyjádřit pomocí nějakého vektoru v, je o něco komplikovanější (tady už nestačí jen vyzobnout směrnici z příslušné přímky) a zaručuje nám to tzv. Rieszova reprezentační věta.
Mimochodem, ty výše uvedené podmínky P3 na duální bázi nám de facto říkají, že první bázový funkcionál (tedy prvek té duální báze) z daného vektoru vypíchne první souřadnici, druhý druhou atd (více zde).
Význam funkcionálů spočívá v tom, že se dají definovat i tam, kde skalární součin nemáme. Místo toho, abychom nějaký pevný vektor u skalárně násobili s různými jinými vektory, tak ho házíme do různých funkcionálů. V obou případech nám z těchto operací vypadne skalár. Abyste si udělali obrázek, jak takový funkcionál v nejlepších letech vypadá, tady je jeden z R3, vyčíslený na vektoru u = {x,y,z}.
F(u) = F({x,y,z}) = 3x-2y+z
Vidíte, že si ho můžete "nasimulovat" skalárním součinem s vektorem {3,-2,1}. Také si všimněte, že výraz F(u)=c je de facto rovnice roviny (v obecnějším případě nadroviny).
Aby se ty duální vektory (kovektory) odlišily od běžných vektorů, obvykle se vizualizují právě pomocí nadrovin, na kterých příslušný funkcionál nabývá nějakou konstantní hodnotu c (tj. pro všechny vektory u z té nadroviny platí F(u)=c). Můžeme si ho tedy představit jako sérii rovnoběžných rovin (se stejnou normálou). Wikipedia má hezkou ilustraci zde (více o vektorech a kovektorech najdete zde - specielně doporučuji odpověď se žlutým pozadím).
Ty kovariantní a kontravariantní souřadnice pak používáme více méně podle toho, zda pracujeme s vektory anebo s kovektory (funkcionály). Mimochodem, i slavné Diracovo značení bra-ket z kvantové mechaniky, kde "bra" je kovektor u a "ket" je vektor v, odráží dualitu vektorových prostorů a je vlastně jen jinou notací pro skalární součin, který ta dualita supluje: <u|v>.
Jinak pokud znáte matice, určitě jste si všimnuli, že na ně můžeme pohlížet buď jako na kolekci řádkových nebo sloupcových vektorů. Podle toho zda maticí násobíme zleva nebo zprava, používáme buď řádky a nebo sloupce a proto dostaneme různé výsledky. I to je odrazem této duality, která se vine celou lineární algebrou jako červená niť. Opravdu otrlé povahy si mohou vzít nějakou ortonormální bázi a poskládat ji do sloupců - tím dostaneme tzv. ortogonální matici (v podstatě rotaci). V řádcích této matice se nám pak objeví duální báze - to je jedna z možností jak si ji konkretně představit (ale to už jsou poměrně zapařené úvahy, se kterými si normální smrtelník nemusí lámat hlavu).
Závěrem ještě (trochu zjednodušenou) poznámku o terminologii.
Vezměme si vyjádření vektoru w v původní bázi u,v
w = au + bv
Když teď ty vektory u a v dvakrát prodloužíme (na 2u a 2v), příslušné koeficienty a,b (tj. souřadnice) musíme dvakrát zkrátit, aby se to vykompenzovalo. Proto se těmto souřadnicím říká kontravariantní (mění se proti smyslu změny vektorů). Ty kovariantní souřadnice se naopak dvakrát prodlouží, protože při prodloužení původní báze se ta duální báze zkrátí (rozmyslete si ty "jedničkové podmínky" v P3'), takže pro daný vektor w musíme použít o něco "větší" souřadnice (abychom si ho z té zkrácené duální báze nabrnkali).
+++++++++
Hudba je takový herbář na vzpomínky. Jsou v ní obtisknuté jako přesličky v uhlí. Nedávno jsem z televize zaslechl jednu povědomou instrumentálku a prakticky okamžitě jsem se přenesl v času i prostoru do Československa 70. let. Už nevím, který televizní pořad měl tuhle melodii jako znělku, ale nezapomenu ji do konce svého života. Je v ní obtisknutý kus mého mládí. Mimochodem, ten maník u dirigentského pultu tu skladbu napsal. Barry White: Love's Theme.
Předchozí díly Matykání
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
Jan Řeháček
Co rok dal

Začátek nového roku je tradičně příležitostí k ohlédnutí za rokem starým, takže jsem prohrábl archív a vylovil z něho pár fotografií z našeho parku, které si nenalezly cestu do některého z předchozích tématických blogů.
Jan Řeháček
Politické školení mužstva: Pyšná princezna

Roto končit! Pozor! (vejde útvarový politruk) Soudruzi vojáci, kapitál se potácí. Ale sám se nám na smetiště dějin nevypotácí. My mu musíme co, soudruzi? No? Nikdo? No, my mu musíme pomoci, vy hlavy hovězí!
Jan Řeháček
Ten podzim se nám hezky vybarvil

Každý podzim je v našem parku trochu jiný. Stromy, které by loni přešminkovaly i šestnáctku před prvním rande, jsou letos pobledlé jako Rusalka. A ty, které se zprvu barevně upejpaly, se najednou utrhly z řetězu. Jak řezníkův pes.
Jan Řeháček
Paroháčů je letos dost

Srnka je v našem parku jako houska na krámě. Zato setkání s jelenem si člověk musí považovat. Letos jsem ale náhodou objevil, kde se srocují: na záložním travnatém parkovišti, kterému se říká Gil's Hill, těsně před západem slunce.
Jan Řeháček
Chřadnoucí prales - pod vodou i nad ní

O korálovém útesu se říká, že je to "dešťový prales" oceánu. Biodiversita, kterou reprezentuje je ohromující. Totéž platí i o jeho suchozemském ekvivalentu. Bohužel, oba ekologické systémy se dostávají na seznam ohrožených druhů.
Jan Řeháček
Letní kvítí

Primární sezónou květů je sice jaro, ale ani léto není v našem parku z pohledu barev úplná nuda. Tady je malá fotovonička složená z příspěvků místní flory. Aneb kdo nekvete s námi, kvete proti nám.
Jan Řeháček
Plody léta

Léto je časem zrání a ani v našem parku tomu není jinak. Zajímavé plody nabízí říše rostlinná i živočišná. Tady je malý průřez letošní nabídkou: asijské maliny, kuriózní houby a malí mývalové. Ceny jsou mírné: léto létá zdarma.
Jan Řeháček
Kvetoucí fuga (Beethoven)

V Beethovenově Misse Solemnis nalezneme spoustu skrytých drahokamů, které zde leží prakticky nepovšimnuty, protože celková hudební struktura této Mše je na první poslech naprosto neprůstřelná. Jedním z nich je fuga v závěru Creda.
Jan Řeháček
Sovy a supi

V našem parku také poletuje spousta zajímavých ptáků. Tak jsem jich pár vyfotil. Sovy jsou sice nočními živočichy, ale na jaře se občas dají zastihnout i za denního světla. A za pár šupů k nim přihodím ještě pár supů. Ať nežeru.
Jan Řeháček
Vlčí západy

Při procházkách naším parkem občas fotím západy slunce z vyvýšeného travnatého parkoviště zvaného Gil's Hill. Říkám jim Vlčí západy. Jednak proto, že mají zhusta barvu vlčích máků a jednak proto, že náš park se jmenuje Vlčí past.
Jan Řeháček
Za devatero fotkami: Malebné peklo

Já to tušil, že jednou skončím v pekle. Jen jsem si představoval, že vstup bude mít z nějaké islandské sopky. Houbeles! Jeho vchod se nalézá poblíž vesničky Medkovy Kopce nedaleko Hlinska. "Lasciate ogne speranza, voi ch'intrate".
Jan Řeháček
Sedm divů jara

Po dlouhém barevném půstu zimní šedi působí návrat jarní kavalerie jako zjevení. V našem parku v tomto období kvete několik dřevin, s jejichž uměleckými kreacemi bych vás v tomto blogu rád seznámil. Matička příroda dokáže kouzlit.
Jan Řeháček
strž

V dnešním pokračování poetického cyklu "Bez básně a Hany" se nedozvíme jakou krevní skupinu mají nejraději novozélandští upíři a zda je tuna pampeliškového chmýří těžší než sbírka maturitních příkladů z matematiky.
Jan Řeháček
Devět zastavení času

Příroda se mění pomalu, ale jistě. Den ze dne nic nepostřehnete, ale když se na známá místa vrátíte za pár týdnů, naleznete desítky drobných změn. Tak jsem se na třech místech našeho parku devětkrát zastavil, abych je zachytil.
Jan Řeháček
Cesta do hlubin duše (Beethoven)

Lidská duše je odvěkou hádankou, na které si vylámaly zuby celé generace psychologů, teologů a filosofů. Tajuplný komplex uvnitř každého z nás. Pro mne je definicí lidské duše Beethovenův 14. smyčcový kvartet cis moll, op. 131.
| předchozí | 1 2 3 4 5 6 7 ... | další |
- Počet článků 402
- Celková karma 19,53
- Průměrná čtenost 920x