Matykání: kam se poděla čtvrtá dimenze?

Čtvrtý rozměr - odvěká vábnička esoteriků, snílků i šarlatánů. Jen se lidstvo domáklo, že Stvořitel utkal náš svět z 3D vaty, začalo spekulovat, jak by vypadala jeho 4D verze. A s hrůzou zjistilo, že by se v ní nedal zavázat uzel.

Kde leží ta bájná čtvrtá dimenze? Už koncem 19. století lidé přemýšleli, jak si takový svět vůbec představit? Naše smyslová zkušenost nás v tomto ohledu nechala trestuhodně na holičkách.

Na první pohled se zdá, že to není nic těžkého. Prostě si ke stávajícím třem směrům (dopředu-dozadu, nahoru-dolů a doleva-doprava) přimyslíme ještě jeden (říkejme mu kubrámu-kešlopsu) a jedem. Tamhle za tou lípou doleva, pak dolů kolem rybníka a hned za hospodou kešlopsu po červené turistické značce. A jsme ve čtvrté dimenzi.

Jenže tak jednoduché to není. Ta čtvrtá souřadnicová osa, řekněme w, na kterou budeme nanášet naši polohu ve směru kubrámo-kešlopsím musí být kolmá k těm předchozím (nebo alespoň nezávislá) a to pro našince s 3D hlavičkou není jednoduché zadání.

Není ale těžké si představit, proč si fantastové schopnosti proniknout do 4D světa tolik cení. Najednou bychom mohli ze zamčeného 3D sejfu ukrást zlaté cihličky a ani bychom se tím nemuseli moc trápit, protože bychom se lehce dostali z jakéhokoliv 3D vězení.

Jak? Podívejme se na to o dimenzi níž.

Takový 2D Rumcajs přijde k nakreslenému sejfu (což je z jeho pohledu 2D obdélník) a protože právě získal propustku do 3D, neprovrtatelnou hranici obdélníka nenuceně překročí, nabere si co potřebuje a zase tu samou hranici překročí nazpátek. A z šatlavy se dostane jakbysmet.

4D bytost by tedy v našem prostoru mohla páchat mnohá alotria. Navíc by do všeho viděla. A to doslova. My například nevidíme své vnitřní orgány, protože jsou obklopeny masem a kůží. Ale přes čtvrtou dimenzi bychom se k libovolnému orgánu mohli přiblížit na libovolně malou vzdálenost a přímo si prohlédnout jeho strukturu a fungování. Stejně jako Ládínek Smolík ze starého kresleného seriálu, když přistál na placaté planetě a do jejích 2D bytostí viděl jak do hubený kozy (viz video).

Takový 4D doktor by na nás 3D smrtelníky vůbec nepotřeboval rentgen.

A na to si musíme posvítit.

(doufám, že vaše myš má v nádrži dostatek benzínu)

+++++++++

Matematika: kartézský součin

Často je užitečné si nějakou množinu představit jako kartézský součin, protože její faktorizace nám umožní nejen najít vhodné souřadnice (a tedy určit její dimenzi), ale i představit si její  vícerozměrné ekvivalenty.

Kartézský součin dvou množin A a B se skládá ze všech uspořádaných dvojic, kde první člen je z první množiny a druhý z druhé:

AxB = {(a,b), kde a?A, b?B}

Nejznámějším příkladem je tradiční eukleidovská rovina, která je kartézským součinem dvou přímek (reálných os). Každý bod roviny je tedy uspořádanou dvojicí reálných čísel {(x,y), kde x?R, y?R}. Pokud si z obou os vybereme pouze jednotkový interval, kartézký součin vytvoří jednotkový čtverec Č=[0,1]x[0,1].

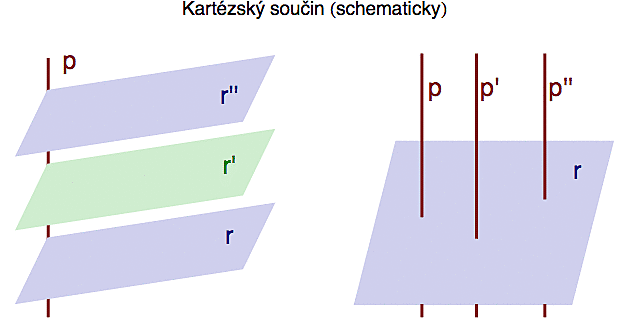
Klasický 3D prostor ve kterém žijeme si - kromě tradiční trojosé verze RxRxR - můžeme představit jako kartézský součin přímky a roviny, tedy RxR2 (na obrázku vlevo vedeme každým bodem přímky rovinu) a nebo naopak roviny a přímky, tj. R2xR (vpravo vedeme každým bodem roviny přímku).

Jak si ty tři souřadnice rozdělíte je na vás. Můžete si buď vybrat na červené ose vlevo bod z a pak v rovině odpovídajícímu tomuto bodu najít bod se souřadnicemi (x,y) a nebo si nejprve v rovině vpravo vyberete bod (x,y) a na přímce procházející tímto bodem pak vyhledáte bod se souřadnicí z. Samo o sobě nám toto strukturální přeskupení žádnou novou dimenzi neposkytne (stejně jako přerovnání bankovek ve vaší peněžence z vás neudělá bohatšího člověka), nicméně když si tuhle "faktorizaci prostoru" dobře rozmyslíte, můžete si pomocí ní vytvořit vlastní konceptuální model 4D prostoru (a zpestřit si tak čekání na Kryštofa Kolumba).

+++++++++

Všechny 2D roviny na předchozím obrázku proměníme ve 3D prostory zvoláním "Dexempo multo federex". Přímky ponecháme přímkami (aby se nám nepřehřál čarodějný modul). A nyní si zkusíme do takto vzniklého hyperprostoru zařadit 4D bod o souřadnicích P=(x,y,z,w). Pokud použijeme jako mustr faktorizaci vpravo, tak si nejprve v tom modrém 3D prostoru r vyhledáme bod P'=(x,y,z). I tímto bodem prostoru prochází jedna červená přímka, po které začneme šplhat (ve směru kešlopsím), až narazíme na hodnotu w. Tam leží bod P. Vaše intuice se té konstrukci možná bude vzpouzet -  přímka procházející bodem P' prostoru r v něm přece musí ležet celá, nemůže z něho nikde "trčet" ven. Ale nenechte se zviklat, naše smysly nám občas našeptávají pěkné nesmysly.

Já osobně pro 4D cestování používám raději tu mapu vlevo. Ráno si na přímce najdu bod w a v prostoru, který je na něj naroubován pak během dopoledne dohledám (x,y,z) - na to mám speciálního ohaře. A do oběda jsem v bodě P.

Já vím - věrný obraz 4D vám to neposkytne. To ani nejde - naše mysl prostě není vybavena softvérem na "prohlížení" 4D prostoru. Ale můžeme o něm na základě této analogie alespoň přemýšlet.

Pokud jsme skutečně součástí nějakého vyššího 4D hyperprostoru, tak na ten náš prostůrek vezdejší můžete nahlížet jako na jeden z těch 3D řezů vlevo. Z téhož obrázku také vyplývá, že do hyperprostoru se vejde obrovská "kupa" běžných 3D prostorů - jeden pro každé reálné číslo w a těch je nespočetně mnoho - dalo by se v něm tedy ubytovat setsakramentsky hodně paralelních vesmírů (jednou jsem se dokonce setkal s blouznivci, kteří tvrdili, že zatímco my žijeme v tom prostoru r, v těch zbylých 3D prostorech se nachází nebe, peklo, ráj, očistec a takové ty bohulibé věci).

+++++++++

Ale vraťme se k tomu doktorovi z úvodu. 4D lékař bude mít možnost vidět kterýkoliv vnitřní bod vašeho těla přímým pohledem (tak jako Ládínek Smolík v citovaném videu).

A není těžké rozmyslet si proč. Jeho pohledu nic nepřekáží.

Představme si, že 3D pacient se nalézá v prostoru označeném vlevo jako r. Bez újmy na obecnosti mu přiřadíme souřadnici w=0. Řekněme, že doktor se potřebuje podívat na bod S=(X,Y,Z,0) ležící uprostřed pacientova srdce. Lékařovo oko (v jednom z těch 3D prostorů "nad" r) bude mít souřadnice L=(x,y,z,w), kde w>0.

A teď stačí si uvědomit, že přímka určená body S a L protíná prostor r pouze v bodě S, takže zbytek trupu (který je v prostoru r ponořen) takto situovanému oku "nezaclání". To je vidět z lehce upravené parametrické rovnice přímky SL, jejíž obecný bod P je

P = tS + (1-t)L, kde t je reálné číslo

Jediný bod této přímky, pro který je w=0 je S (ten dostaneme volbou t=1). Všechny ostatní body (dosadíme-li t?1) mají nenulové w a leží tedy mimo prostor r. Pokud si doktor do optické dráhy SL sám omylem nestrčí noviny, bude mít nezakrytý výhled na bod S. Musí si ho ale nasvítit 4D baterkou.

Obyčejný 3D doktor takovou perspektivu nemá. Jeho oko je součástí prostoru r, řekněme v pozici L'=(x,y,z,0). V tomto případě je w=0 pro každé t a přímka SL' (která leží celá v prostoru r) se musí chovat jako slušně vychovaná 3D množina.

Z pohledu 3D doktora je bod S vnitřním bodem těla - tj. existuje malé okolí bodu S, které je zcela uvnitř (a proto našemu zraku skryté). Přímka SL' z doktorova 3D oka by posledních pár centimetrů musela "projíždět" tělem pacienta. To přímka SL dokáže tělo "objet", takže 4D doktor nás nemusí "kuchat", aby se dostal k bodu S (více o tom v sekci Jauvajs).

+++++++++

Pokud doma v garáži  po večerech "svařujete" vektorové prostory pomocí kartézského součinu, bude vás zajímat, jak se do výsledného monstra zavede lineární struktura (tj. jak se tam definují vektorové operace). To se v lineární algebře dělá pomocí tzv. přímého (direktního) součtu dvou prostorů V?W (direct sum), ve kterém je sčítání a skalární násobení automaticky zkombinováno z operací na prostorech V a W, takže lineární kutil si s tím nemusí lámat hlavu.

Kartézský součin je ale velice obecná množinová konstrukce, kterou můžete aplikovat prakticky na cokoliv - například na množinu všech lichoběžníků L a množinu všech kopretin K. Na součinu LxK by se ovšem dimenze zkoumala těžko. Proto si z minule připomeňme torus, na který se můžeme dívat jako na kartézský součin dvou kružnic SxS (to si představte buď tak, že každý bod první kružnice je nahrazen tou druhou anebo že ke každému bodu jedné kružnice je "přivařena" kružnice druhá). Bod na povrchu toru odpovídá dvojici bodů (a,b), kde a leží na jedné kružnici a b na druhé. A protože bod na kružnici se dá ocejchovat jedním číslem, vyjde nám 2D torus (což jsme minule vydedukovali z toho, že se lokálně podobá rovině).

+++++++++

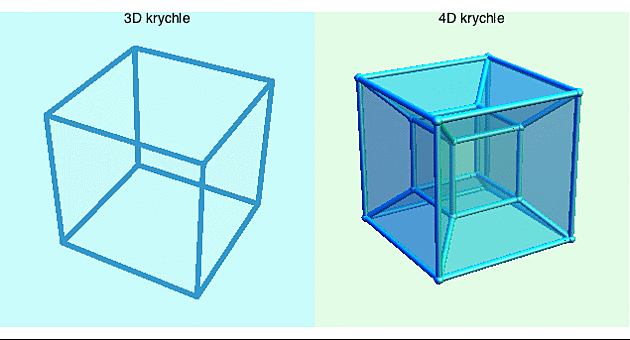
Další užitečnou pomůckou pro nahlédnutí do 4D prostoru je jednotková hyper-krychle (tedy kartézský součin 4 jednotkových intervalů [0,1]). Podívejme se nejprve na její ekvivalenty v nižších dimenzích.

2D krychle je vlastně klasický jednotkový čtverec, tedy kartézký součin [0,1]x[0,1]. 3D krychli si pak sestavíme tak, že vezmeme dva tyto čtverce, umístíme je nad sebe a jejich 4 rohy spojíme úsečkami (obr. vlevo).

A teď směle do 4D (vpravo). 4D krychli si analogicky postavíme tak, že vezmeme dvě 3D krychle, umístíme je "vedle" sebe (přesněji tak, aby jedna byla kešlopsu druhé) a jejich osm rohů spojíme úsečkami. Pak zhruba dvě minuty mumláme "dexempo multo šumpoplex" a máme na stole 4D krychli. Vidíte, ani to nebolelo. Říká se jí teserakt.

Obrázek 3D krychle i 4D teseraktu je samozřejmě sám o sobě pouze 2D. Lépe si tu "prostorovost" krychle vychutnáme, pokud necháme obrázek rotovat (kdo nikdy neviděl rotující krychli, mrkněte sem). Stejně tak je pro pochopení 4D teseraktu užitečné zapnout fantazii na plný výkon a nechat tu kostru vpravo otáčet v hyperprostoru (viz zde nebo zde a nebo s anglickým výkladem na YouTube).

A ne abyste do té rotující hyper-krychle strkali šroubovák. Kdo bude teserakt sabotovat, zůstane 300 let po škole a bude v přírodopisném kabinetu krmit další 4D kartézskou příšerku jménem duocylindr (a nemyslete si, že je to jen nějaký neškodný filcový klobouk pro dvojčata - duocylindr dokáže schramstnout i dospělou chobotnici). No a my ostatní zatím odhodíme svůj algebraický širák v dál a podíváme se, jaké jsou šance na nalezení 4D prostoru ve fyzice.

+++++++++

Fyzika: prostoročas

První na ráně při hledání čtvrté dimenze je prostoročas, na který se my, nešťastníci fyzikou nepolíbení, díváme jako na kartézský součin 3D prostoru a času.

Jeho body nazýváme "události", protože mají kromě tří běžných prostorových souřadnic x,y,z také časovou souřadnici t a celá tato suita je úhledně poskládána do balíčku, kterému fyzici říkají čtyřvektor.

To celkem odpovídá naší naivní představě, že vše, co se kolem nás děje se dá lokalizovat v čase i prostoru. Z formálního pohledu má sice prostoročas malý nedostatek v tom, že není jasné, kde by měl mít vlastně počátek, takže mnozí fyzici se na něho dívají spíše jako na afinní než vektorový prostor, ale s tím si nebudeme lámat hlavu.

Prostoročas má totiž jednu podstatně větší mouchu.

Při zkoumání geometrie 3D prostoru hrají důležitou roli transformace, které zachovávají úhly a vzdálenosti a kterým se technicky říká Eukleidova grupa (v angličtině o něco příhodněji rigid motions). Můžete si je představovat jako translace a rotace, které s pevným objektem dokáží posunovat sem a tam, ale nedeformují ho.

V prostoročasu, jak ukázala speciální teorie relativity, ale operuje o něco komplikovanější Lorentzova grupa a ta s našimi klasickými představami o rigidnosti prostoru a času těžce zatočila. Dříve absolutní rozměry se deformují jako by byly z lískového těsta a to, co rozumíme pod pojmem "velikost vektoru", nemusí být nutně invariantní (tedy odolné vůči relativistickým transformacím). Naštěstí se ukázalo, že tu invariantnost získáme zpátky, pokud si "velikost" čtyřvektoru nebudeme definovat po eukleidovsku jako

(1) || (x,y,z,t) ||2 = x2 + y2 + z2 + t2

ale spočítáme si ji v mírně pozměněné formě

(2) || (x,y,z,t) ||2 = x2 + y2 + z2 - t2

(hyperbolický charakter pravé strany není zase takovým překvapením, uvážíme-li, že Lorentzova transformace je de facto hyperbolická rotace)

Výraz (2) tedy přebírá roli Eukleidovské normy (1), a obvykle se definuje pro rozdíl mezi dvěma prostoročasovými událostmi (tomu se říká "interval", ale pro jednoduchost se na něj budu i nadále dívat jako na vektor, aby bylo lépe vidět, v čem to matematicky hapruje - a ze stejného důvodu jsem rychlost světla c položil rovnou 1). Prostorům, kde vládne norma typu (1) se říká Eukleidovské, tam kde vládne norma typu (2) mluvíme o Minkowského prostoru.

Předminule jsme si řekli, že norma (a s ní související skalární součin) určuje geometrii prostoru. Jakákoliv změna v definici se tudíž citelně projeví na jejích vlastnostech (i pouhé prohození znaménka dokáže při výpočtu natropit pěknou paseku). Mohli bychom si sice vymyslet imaginární čas it, který by to dal Eukleidovsky do cajku - protože i2=-1, takže z (2) by se stalo (1) - ale takové formální světočarování mi přijde trochu zavádějící.

+++++++++

Podívejme se raději, jak se prostory s těmito dvěma typy norem od sebe liší.

Aby se to dalo lépe nakreslit (a taky počítat), zapomeňme na prostoročas a přesuňme se o dimenzi níže. Porovnejme si 3D Eukleidovský prostor, kde je norma vektoru u=(x,y,z) definovaná jako

(1') N(u)2 = || (x,y,z) ||2 = x2 + y2 + z2

s 3D ekvivalentem Minkowského prostoru, kde bude

(2') N(u)2 = || (x,y,z) ||2 = x2 + y2 - z2

Zatímco v Eukleidovském prostoru mají všechny nenulové vektory kladnou velikost, v Minkowského verzi mohou mít velikost kladnou, nulovou i zápornou. Jakkoli to zní absurdně, existuje v něm množina nenulových vektorů, které mají velikost nula - a je jich celý pytel, respektive kužel (N(u)=0 je totiž rovnice kuželu). Pokud si chcete osahat nějaké konkretní exempláře, představte si libovolnou Pythagorejskou trojici: (3,4,5), (5,12,13), (8,15,17),... - to všechno jsou nenulové vektory "redukovaného" Minkowského prostoru s nulovou délkou (ta je mimochodem v rozporu s definicí normy a proto se veličině definované vzorečkem (2') říká pseudonorma).

V čase z se světlo (šířící se z bodu (0,0) rychlostí c=1) dostane do bodů (x,y), jejichž vzdálenost od počátku splňuje

sqrt(x2+y2) = z  neboli x2+y2-z2 = 0

a to je přesně pseudonorma (2'). Pokud by byla záporná, stačila by nám k dosažení (x,y) v čase z podsvětelná rychlost, pokud kladná, museli bychom cestovat nadsvětelnou rychlostí (a to nelze).

Fyzika si z porovnání se šířením světla vytvořila hezkou klasifikaci. Vektorům s nulovou pseudonormou říká "světelné", protože dvojice událostí, jejichž rozdílem vzniknou mohou být spojeny pouze prostřednictvím světelného paprsku. Vektorům se zápornou pseudonormou říká "časového charakteru" a příslušné dvojice událostí mohou být spojeny podsvětelným signálem, zatímco vektory s normou kladnou ("prostorového charakteru") reprezentují události, které nelze spojit signálem vůbec. Takový zvěřinec v Eukleidovském prostoru nenajdete. Tam jsou si všechny vektory před normou rovny.

Abychom ten rozdíl v normách viděli na vlastní oči, podívejme se na množinu jednotkových vektorů v obou prostorech. Jednotkový vektor splňuje rovnici N(u)=1 a v Eukleidovském prostoru se nachází na jednotkové sféře, zatímco v (redukovaném) Minkowského prostoru leží na povrchu jednolistého rotačního hyperboloidu (na obrázku z něho vidíme jen kousek).

Podobně by to dopadlo, kdybychom namísto jednotkové koule N(u)=1 zkoumali množinu "malých vektorů", splňujících N(u)=0.01. Pak by ty obrázky (které by vypadaly prakticky stejně, jen by měly jinou škálu) ukazovaly "malé okolí" počátku. V Minkowského prostoru se do něho ale vejdou i vektory s libovolně velkými souřadnicemi a to trochu dráždí naše pojetí "lokálnosti" (lokální by mělo být něco, co se šmrdlá v okolí daného bodu). To Minkowského "okolí" - nazíráno Eukleidovskýma očima - lokálně vůbec nevypadá. Ale to se ve světě, kde nenulové vektory mohou mít nulovou délku dá očekávat.

Ta "zvláštní" definice pseudonormy v Minkowského prostoru si vyžaduje také "zvláštní" skalární součin, který musí to závěrečné mínus zohlednit:

(3) u.v = u1*v1 + u2*v2 - u3*v3

Pokud se vám zdá, že ani toto není nijak drastická změna, uvažte, že vektory

u = (1,4,4), v = (4,7,8) a w = (4,8,9)

jsou v Minkowského prostoru navzájem pravoúhlé - v tom smyslu, že jejich skalární součin (3) je nula. V Eukleidovském prostoru by nebyly pravoúhlé ani náhodou (a protože pseudonormy těchto vektorů jsou 1, 1 a -1, dohromady tvoří určitou obdobu ortonormální báze). Celá Eukleidovská geometrie, pro kterou máme z praktického života poměrně solidní intuici je zde postavena na hlavu: to, co nevypadá jako kolmé, je kolmé a to, co nevypadá jako krátké, je krátké.

(zajímá-li vás odkud se ty tři vektory vzaly, pronásobte si tyto matice)

+++++++++

Nic vám samozřejmě nebrání se na Minkowského prostoročas dívat jako na 4D vektorový prostor, ale jeho geometrické vlastnosti jsou natolik divoké, že takový pohled moc nedoporučuji. Žádné matematické kouzlení nic nenadělá s tím, že čas je trochu jiný typ zvířátka než prostor (i když ho pronásobíme rychlostí světla, aby se na metro dalo čekat v metrech a ne v sekundách).

To je taky jeden z důvodů, proč čas nemůžete použít k pohledu "dovnitř" uzavřených 3D objektů, jako v tom příkladu s 4D doktorem. Pokud už dvě hodiny toužebně přešlapujete před zamčenými dámskými sprchami - pánové, mluvím teď k vám - tak ty poctivě natažené kukačkové hodiny zase schovejte do krabice a dejte si padla.

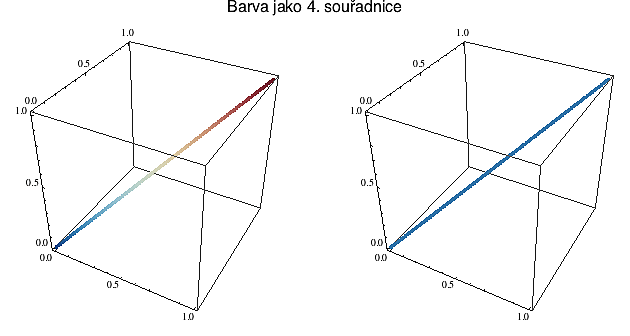
Nicméně myšlenka, přidat k prostorovým souřadnicím něco z trochu jiného soudku má ve vizualizaci 4D jednu zajímavou aplikaci. Ne - nemyslím tím, že bychom ke každému bodu přidali jeho teplotu a vytvořili tak teploto-prostor. Ale přihořívá. My si tu chybějící čtvrtou dimenzi představíme jako barvu (což je také určitý typ informace, stejně jako prostorová souřadnice).

To znamená, že bod B=(x,y,z,w) vyneseme do polohy (x,y,z) a obarvíme ho barvou, kterou odvodíme z hodnoty w (např. podle nějakého barevného schematu, kde w=0 bude odpovídat prostředku škály, zatímco pro hodnoty w<0 zvolíme chladnější barvy vlevo a pro w>0 teplejší barvy vpravo).

Na dalším obrázku vidíme v tomto provedení dvě 4D přímky. Na té vlevo se mění všechny 4 souřadnice, takže se kromě x,y a z mění i její barva, zatímco na té vpravo zůstává barva stejná (souřadnice w je na této přímce konstantní).

V intencích dnešního prvního obrázku to znamená, že levá přímka prochází napříč všemi 3D prostory r,r',r''... zatímco ta vpravo leží celá v jednom jediném 3D prostoru r (má konstantní w).

Podobnou možností je zobrazit 4D bod B=(x,y,z,w) na kouli se středem v bodě  (x,y,z) a s poloměrem w (ten bude hrát roli "barvy"). Tímto způsobem sice zabydlíme pouze "horní část" 4D prostoru (w>0), ale zato pomocí důvěrně známých objektů. A kdo na ty koule nemá koule, může zkusit něco jiného.

Ta kolečka v hlavě máme všichni nastavený trochu jinak, takže nejvhodnější vizualizaci 4D prostoru si musí každý vybrat sám (spousta lidí se v něm například orientuje pomocí 3D průmětů - viz toto video).

+++++++++

Fyzika: teorie strun

Dobrá, čas nebrat.

Fyzika má ale ještě jedno eso v rukávu, které nám nabídne skutečnou prostorovou hostinu. Ne jednu extra dimenzi, ale hned šest, neřkuli sedum. Podívejme se ale nejprve na malý prototyp.

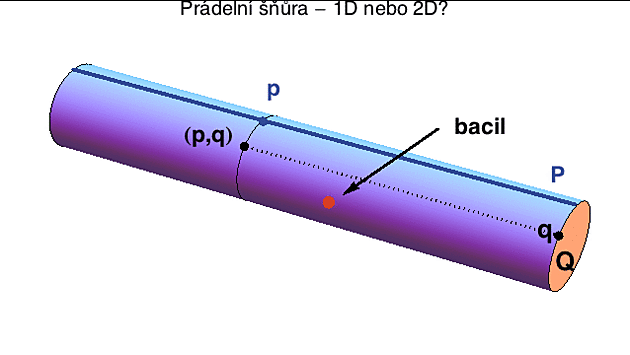
Vezmeme si běžnou prádelní šňůru. Z pohledu hospodyně se jedná o 1D objekt. Aby udala polohu visících ponožek, stačí jí jediné číslo (ponožky visi 87 cm od pravého stojanu).  Teď si ale představme, že po šňůře leze malý bacil a chce svou polohu zatelefonovat kolegovi, aby mohli prostřednictvím ponožek pana Foustky provést invazi do lidského organismu (za to by ho jeden rovnou bacil). Tady už nestačí zahlásit "jsem 87 cm od pravého stojanu". Bacil musí dodat ještě jedno číslo: kde se nalézá podél obvodu šňůry (který je z bacilího pohledu značný).

V bacilosvětě je ta prádelní šňůra vlastně kartézským součinem přímky P a kružnice Q (viz obrázek), takže každý bod si lze představit jako uspořádanou dvojici (p,q), kde p je bod na přímce a q je bod na kružnici. A protože bacilové nejsou žádní imbecilové, používají pro specifikaci q středový úhel - s tím, že ho měříme v radiánech proti směru hodinových ručiček a přímka P odpovídá 0.

Prádelní šňůra je z pohledu matematiky protáhlý válec s konstantním poloměrem r a ta uspořádaná dvojice (p,q) se dá lehce přeložit do cylindrických souřadnic z,? (kde z je vzdálenost od stojanu a ? je zmíněný úhel).

Otázkou zůstává, zda se máme na tu šňůru dívat jako na 1D nebo 2D objekt. To je matematice vcelku jedno. Záleží na tom, jaký problém řešíte a podle toho si vyberete, zda použít 1D model (vhodný pro hospodyně) a nebo 2D model (vhodnější pro bacily).

Zajímavé je, že ty dvě dimense bacilího modelu nejsou úplně rovnoprávné. Dimenze "podél šňůry" je v principu nekonečná (nebo alespoň libovolně dlouhá), zatímco ta podél obvodu je konečná (a v jistém smyslu "svinutá"). Nám, co jenom sušíme prádlo, je ta "svinutá" dimenze pochopitelně na houby. Pro teorii strun ale její existence leží v samotném srdci úvah o našem prostoru.

+++++++++

Historie teorie strun začíná v podstatě tam, kde jsme v předchozí sekci skončili. V roce 1916 publikoval Einstein obecnou teorii relativity, jejímž výsledkem bylo, že na gravitaci se můžeme dívat jako na volný pohyb v zakřiveném prostoročasu (ze kterého se tím pádem stává pseudo-Riemannova varieta - tedy něco, co se lokálně podobá ne Eukleidovskému, ale Minkowského prostoru). O pár let později Theodor Kaluza ukázal, že pokud bychom rozšířili prostoročas na 5 dimenzí (tj. čas plus 4D prostor), dal by se do geometrické teorie zahrnout i elektromagnetismus (mimochodem, tato myšlenka se dá vystopovat až k poměrně zapomenutému Gunnaru Nordströmovi).

Jenže kde ty 4 prostorové dimenze vzít, když je kolem sebe nikde nevidíme a ani nejsme schopni je detekovat. S těmito pochybami skoncoval v roce 1926 Oscar Klein, který postuloval, že chybějící dimenze je ve skutečnosti "svinutá", takže ji nevidíme a v podstatě ji ani nemůžeme nijak prakticky využít (stejně jako hospodyně věšící prádlo má k disposici pouze tu "rozbalenou" dimenzi).

Teorie strun, která na tento směr úvažování navázala v 60. a 70. letech minulého století, předpokládá, že svět ve kterém žijeme má ne jednu, ale hned 6 svinutých dimenzí. Prostor je tedy v podstatě kartézským součinem R3xC (podobně jako bacilova šňůra byla součinem PxQ), jen s tím rozdílem, že místo 1D šňůry máme 3D prostor a ty svinuté dimenze nežijí na kružnici (či nějaké hypersféře), ale na poměrně komplikovaném (a malilinkatém) 6D útvaru C, kterému se říká Calabi Yau varieta (na 2D animaci se můžete podívat zde). Společně s časem a obvyklým 3D prostorem (ke kterému jsou tyto 6D potvůrky v každém bodě kartézsky "přivařeny") pak tvoří 10D prostoročas, ve kterém se teorie strun odehrává (dokonce se zdá, že by to díky tzv. M teorii mohlo být až 11D).

A proč je těch dimenzí tolik?

Strunisté se na částice dívají jako na miniaturní kmitající struny, jejichž vibrační módy určují vlastnosti elementárních částic. To kmitání ovšem neprobíhá někde v koncertní síni, ale na povrchu Calabi-Yau variet a to znamená, že jejich vnitřní struktura musí být dostatečně bohatá, aby se tím kmitáním dala vysvětlit celá částicová fyzika. A dimenze tomu napomáhá - čím je vyšší, tím bohatější je škála možností. V jedné dimenzi toho moc nenavibrujete, ve dvou už se dá ledacos podnikat, ve třech to začíná být zajímavé, ve čtyřech už můžete se strunami provádět psí kusy, v pěti ještě psejší a v šesti úplně nejpsejší. A tak se ta svinutá varieta ustálila na 6D (zatím).

Aby to bylo jasnější, podívejme se na jednu hrubou analogii. Vezmeme si dvě obruče, jednu umístíme do duté sféry a druhou navlékneme na torus. Pokud je všechno dobře promazané, tak se obě obruče budou moci v určitých limitech pohybovat. Každá z obou variet ale umožňuje obručím jiný typ otáčení. A podobně různé typy Calabi-Yau variet umožňují strunám různé typy kmitání.

Toto je ale zatím pouze jedna z teorií, takže na konečný verdikt o povaze našeho prostoru si asi budeme muset ještě pár dekád počkat.

++++++++++

Matematika: Kleinova láhev

Když přijdete k očaři abyste zjistili, jak je na tom váš 4D zrak, pravděpodobně před vás postaví Kleinovu láhev a zeptá se, co vidíte.

Kleinova láhev je vícedimenzionální variantou známějšího Möbiova pásku. Tak jako ten pásek nemá rub a líc, protože jedno přechází v druhé, láhev nemá - ze stejného důvodu - vnitřek a vnějšek (přesto se dá při troše dobré vůle vytvořit ze skla, ba i naplnit).

Na počátku její matematické reprodukce stojí (stejně jako u Möbiova pásku) jednotkový čtverec, jehož strany určitým způsobem slepíme (viz obrázek vpravo). Pokud čtverec v červeném směru trochu natáhneme a pak slepíme pouze pouze modré strany, tak aby si naznačené šipčičky sedly přesně na sebe, dostaneme Möbiovu pásku.

Při výrobě Kleinovy lahve slepíme naopak nejprve strany červené (což je jednodušší, protože ty nemusíme kvůli tomu opačnému směru překrucovat), takže dostaneme malý válec a ten opět trochu protáhneme. Když takto vzniklou rouru vezmeme do rukou, držíme vlastně hadici od vysavače. A teď se pokusíme slepit ty modré hrany (ze kterých se mezitím staly koncové kružnice válce). Nejpřirozenější by bylo oba konce té hadice prostě přiložit k sobě a slepit je (tímto bychom de facto dostali torus). Jenže těsně před tím než k sobě oba konce přiložíme, tak si všimneme, že ty šipčičky, které nám ukazují jak je slepit, jdou opačným směrem.

Tudy tedy cesta nevede.

Jediný způsob jak ty konce slepit (aby si šipčičky na sebe "sedly") je představit si, že držíme  "ducha" vysavačové hadice, který umí procházet sám sebou, a jeden konec "proneseme" tím druhým (při tom je oba stále držíme otvorem vzhůru). Teď už nám ty šipčičky "sedí", takže jakmile oba konce "zarovnáme", slepíme je rychlolepidlem a máme Kleinovu láhev (podrobněji je to popsáno zde).

To jste netušili, že matematika se zabývá posmrtným životem vysavačových hadic, co?

Tady je konečný výsledek.

Kleinova láhev se ve 3D nedá realizovat jako 2D varieta (tedy neprotínající se plocha), v podstatě ze stejného důvodu jako se osmička z minulého Matykání nedala realizovat v 2D jako 1D varieta. Tam jsme ji museli přemístit do 3D a jeden oblouk osmičky v tom zkřížení trochu "povytáhnout" nahoru. Tím jsme z ní dostali něco jako uzoučkou autodráhu, která už se lokálně podobala kousku přímky.

Abychom se vyhnuli tomu "duchařskému" protnutí, budeme muset Kleinovu láhev přemístit do 4D a udělat s ní vpodstatě totéž - tedy jeden její kousek "přizdvihnout" (ve směru kešlopsím). A opět si tu čtvrtou dimenzi (reprezentovanou souřadnicí w) představíme jako barvu.

Jak jsme si řekli výše, Kleinova láhev je více méně takový podivně slepený válec. Na začátku ji celou necháme ve 3D (to znamená že w=0) a bude mít tudíž stejnou barvu, řekněme červenou. A teď podél toho válce budeme posunovat elastický barvicí náramek. V okamžiku, kdy nám bude hrozit, že se protneme s jiným kouskem, začneme měnit barvu láhve. V té vrchní části obrázku vidíte, že ta tubice, jakmile se obrátí dovnitř, potřebuje projít vlastní stěnou, aby se dostala ven. A za tím účelem ji pomocí náramku přebarvíme do modra, bez kolize ji protáhneme stěnou a jakmile jsme venku, barvu zase navrátíme původnímu tónu. Tam, kde by ve 3D došlo k průniku se stávajícím tělem lahve, se ve 4D dokážeme "vyhnout", protože ty různé barvy znamenají, že obě zdánlivě se protínající části mají různou souřadnici w. Podařilo se nám část lahve natlačit kešlopsu a průniku jsme (ve 4D) zabránili.

Tady si mimochodem můžeme vypomoci s prostoročasem. I když čas není úplně to pravý prostorový vořechový, dává nám jakous takous čtvrtou souřadnici a pokud si uděláme animaci nejbližšího okolí našeho "náramku", uvidíme i zde, že se protnutí dokážeme lehce vyhnout, protože tou spornou oblastí ve 3D prostoru (kterou si nárokují dva kusy lahve) projedeme v různých časech (tady to máte jako video na wiki). Jinými slovy, pokud tu lahev tvoříme postupně, okamžik za okamžikem, protnutí se lehce vyhneme.

Takže ve 4D je Kleinova láhev zcela legitimní 2D varietou bez "samoprůniku" (ten vzniká teprve projekcí zpět do 3D - stejně jako když mimoúrovňovou autodráhu promítnete do 2D podlahy a získáte křížící se "osmičku").

Jak Kleinova lahev, tak Möbiova páska, patří k neorientovatelným povrchům a mají tu krásnou vlastnost, že dokáží "prohodit" pravolevost - například z kraba s klepetem vlevo udělají kraba s klepetem vpravo a to pouhým pohybem po prostoru (viz známá animace na wiki). S Möbiovou páskou si to můžete zkusit sami - tu si slepíte raz dva.

+++++++++

A když jsme ve 4D dokázali "rozseparovat" Kleinovu láhev, dokážeme v této dimenzi také rozmotat libovolný uzel.

Podívejme se na první dva uzly na dalším obrázku.

Tomu vlevo (a) se říká triviální uzel, protože to vlastně žádný pořádný uzel není. Prostě ten provázek popadneme, trochu s ním zatřepeme a "uzel" je pryč. Matematicky vzato to znamená, že se tento uzel dá spojitě zdeformovat na běžnou kružnici bez protnutí (tedy, že ten provázek neprojde sám sebou jako "duch").

Ten druhý (b) už triviální není. Tam s tím provázkem můžeme třepat jak chceme a zauzlení se nezbavíme. Jedním z úkolů teorie uzlů je ukázat, že ve 4D se každý uzel dá spojitě zdeformovat na uzel triviální (aniž by se musely použít nůžky).

Když se podíváte na ten prostřední uzel, vidíte, že by úplně stačilo, kdyby se nám podařilo to "křížení" uprostřed severní části uzlu prohodit tak, aby se ta "spodní" část dala spojitě (a bez protnutí) přemístit nad tu "vrchní". Pak už by to byl triviální uzel, se kterým by se zatřepalo a byl by fuč (to si můžete klidně zkusit s kouskem provázku). 

Ve 3D se nám ta "změna zkřížení" nepovede (museli bychom ten provázek nejdřív zabít a udělat z něj "ducha"). Ve 4D už to půjde a opět si vypomůžeme s barvami.

Na počátku necháme celý uzel sedět v 3D prostoru r (z dnešního prvního obrázku), takže pro něj bude w=0 a celý provázek bude červený. A teď budeme pomalu tu spodní část severní křižovatky zdvihat nahoru a při tom budeme současně měnit její barvu tak, že v okamžiku kdy "skoro narazí" na tu vrchní část už nebude červená. Bude mít jinou souřadnici w (než ta část do které jsme málem narazili) a k žádné nežádoucí kolizi nedojde.

Obě části provázku se dokázaly "barevně" vyhnout a po úspěšném průchodu opět barvu spojitě stáhneme do červené a máme provázek s triviálním uzlem (sedící v původním 3D prostoru r). Zatřepeme jím a simsala bim - uzel je fuč.

Toto "kouzlo" se dá opakovaně provést i pro velmi komplikované uzly (třeba uzel c, kterému se odborně říká "gordický"), takže ve 4D je každý uzel triviální. Pokud vám vrtá hlavou, proč nás ještě nekontaktovala žádná 4D civilizace, vysvětlení je nasnadě. Čtyř-rozměrňáci si nemohou udělat uzel na kapesníku a tak na to zapomněli.

+++++++++

Sekce Jauvajs: není metrika jako metrika

(pouze pro majitele myší s mimořádně velkou nádrží)

Dnes jen stručné zopakování několika faktů roztroušených po předchozích Matykáních.

Ve vektorovém prostoru je měření vzdáleností realizováno pomocí polohových vektorů. Vzdálenost mezi dvěma vektory x a y je norma (délka) rozdílového vektoru:

d(x,y) = || x-y ||

Velice brzo ale matematikům došlo, že pro měření vzdáleností není potřeba definovat celou tu lineární mašinérii. Bohatě by stačilo mít funkci dvou proměnných d(x,y), která by dvěma bodům daného prostoru (ne nutně vektorového) přířadila nezáporné číslo, vyjadřující jejich vzdálenost. Takové funkci říkáme metrika a předchozí rovnice je jejím příkladem. Například na jednotkové kružnici (která není vektorovým prostorem) se dá metrika zavést pomocí středového úhlu sevřeného mezi body x a y. Množina, na které se dá metrika zavést, se pak přirozeně jmenuje metrický prostor.

K nejdůležitějím pojmům analýzy metrického prostoru M (a analýzy obecně) patří okolí bodu x, které je obvykle realizováno "koulí" o poloměru r

B(x,r) = {y?M, d(x,y) < r}

Tu kouli jsem dal úmyslně do uvozovek, protože podmínky pro metriku jsou poměrně volné a mnohé metrické prostory mají tak nestandardní chování, že množina B(x,r) vůbec nemusí "vypadat jako koule". Nicméně pokud je metrika Eukleidovská, tak je to okolí skutečně tradiční n-dimenzionální koule (tj. v 1D je to interval kolem bodu x, ve 2D je to kruh kolem něho, ve 3D koule a od 4D dál hyper-koule).

+++++++++

Bodu x z množiny M říkáme vnitřní bod, pokud existuje nějaké jeho okolí B(x,r), které je celé součástí M (neformálně: vnitřní body jsou ty, které neleží na hranici M). Pokud má nějaká množina pouze vnitřní body, říká se jí otevřená množina. Otevřená množina tedy nemá hranici (nebo "slupku" chcete-li). Ty hraniční body jsou právě ty, ke kterým se dá libovolně blízko přiblížit jak z vnitřku, tak z vnějšku množiny M a nedá se pro ně tedy najít okolí, které by je od vnějšku "izolovalo".

Příklad: M bude uzavřený interval [0,1]. Hraniční body 0 a 1 nejsou vnitřní, protože se nedá najít žádné jejich okolí, které by bylo kompletně součástí [0,1]. Všechny ostatní body jsou vnitřní: pro 0<x<1 si stačí zvolit dostatečně malé kladné r, tak aby koule B(x,r) "nepřečuhovala" přes hranici intervalu. Z této diskuse také vyplývá, že otevřený interval (0,1) je otevřenou množinou, jak asi očekáváme.

Stojí za zmínku, že otevřenost sama o sobě závisí na povaze metrického prostoru (a v případě lineárního prostoru na jeho dimenzi). O tom už jsem se trochu zmínil minule (v sekci "Jak ohnout vektorový prostor").

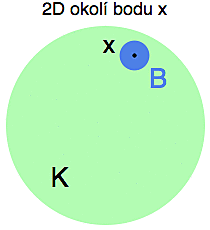
Na obrázku vpravo vidíme otevřený jednotkový kruh K v R2 (tj. kruh o poloměru 1 se středem v počátku a bez hraniční kružnice). Bod x=(0.3,0.7) je vnitřním bodem tohoto kruhu v R2, protože si můžeme vzít např. r=0.15 a celé modré okolí B(x,r) bude stále součástí kruhu K (v kontextu metrického prostoru R2). Všimněte si, že ve 2D to okolí bod x zcela izoluje od zbytku roviny.

Ve 3D už ho neizoluje - svrchu se k němu lze dostat.

Podívejme se na ten samý obrázek v kontextu metrického prostoru R3 (ve kterém samozřejmě existuje jak ten jednotkový 2D kruh K, tak zvolený bod). Tady už x vnitřním bodem není, protože okolí B(x,r) nyní reprezentuje malá 3D koule a ať je její poloměr r sebemenší, do plochého 2D kruhu K ji nenabušíme ani kladivem. A to v R3 platí pro všechny body kruhu K (který přechodem do vyšší dimenze ztratil svoji otevřenost - to se mimochodem občas přihodí i politikům).

A právě tato lapálie stojí za (v úvodu zmíněnou) možností 4D doktora nahlížet do lidského těla. Tak jako má 2D kruh jiné vlastnosti v 2D a jiné v 3D, lidské 3D tělo se bude jinak jevit 3D doktorovi a jinak jeho 4D kolegovi. Ve 3D je srdeční bod S vnitřním bodem lidského těla, ve 4D už ne (protože každá malá 4D kulička kolem S trochu vyhřezne mimo 3D tělo). Z pohledu 4D naše tělo nemá vnitřní body, takže 4D doktor ho má jako na dlani. Pokud bychom před ním naše orgány chtěli skrýt, museli bychom si pořídit 4D maso.

+++++++++

Pojem "okolí" se pro analýzu ukázal být natolik důležitým, že matematici na něm vystavěli ještě jednu vrstvu abstrakce. Došli totiž k závěru, že vlastně nepotřebují ani tu metriku; že by jim bohatě stačilo, kdyby jim někdo s každým bodem podal seznam jeho okolí a bylo by vystaráno. A to je v podstatě základem pojmu topologický prostor (někdy se místo seznamu okolí definuje pomocí seznamu otevřených množin). Abychom se mohli plně soustředit na "tvarové" vlastnosti objektu, zcela jsme se vzdali pojmu "vzdálenost".

A prošlo to - třeba definice spojitosti skutečně metriku nepotřebuje: funkce y=f(x) je spojitá pokud ke každému okolí bodu y existuje okolí bodu x, které se do něho (funkcí f) kompletně zobrazí. Pokud ale tu metriku máte, tak si ta okolí realizujete pomocí koulí s poloměrem ? a ? a získáte tradiční (a mezi studenty obávanou) epsilon-delta definici spojitosti.

++++++++++

Závěrem ještě jedno malé varování.

V diferenciální geometrii (a také v obecné teorii relativity) se pojem metrika používá v trochu jiném významu.

Minule jsme si řekli, že většina variet (říkáme jim Riemannovské) umožňuje v tečném prostoru definovat skalární součin a tím pádem také normu - tj. nástroj na měření délky vektorů.

Pokud si tečný prostor k varietě M v bodě p označíme TpM, můžeme se na ten skalární součin dívat jako na funkci definovanou na kartézském součinu (tj. dvojicích vektorů)

g: TpM x TpM --> R

kde g(u,v) je ten skalární součin - tedy reálné číslo, které jsme dříve označovali u.v. Proč tomu teď najednou říkám g uvidíte za chvilku.

My jsme ze střední školy zvyklí, že skalární součin je něco, co funguje všude stejně. A v Eukleidovském prostoru tomu tak skutečně je. Spočítáte si g(u,v)=u.v pro dva vektory, pak je posunete o 20,000 mil na severozápad a jejich skalární součin bude stále stejný.

U variet to tak ale obecně být nemusí. Pokud z bodu p popolezete o 20,000 mil na severozápad do bodu q, tak se může lehce stát, že skalární součin v "novém" tečném prostoru TqM bude fungovat úplně jinak (například bude mít nějaké jiné koeficienty: u.v = 2*u1*v1+3*u2*v2). Jinými slovy to "g" z definice skalárního součinu v tečném prostoru závisí na p - správně bych to tedy měl zapisovat jako g(p) (kdybych ten skalární součin značil pouze tečkou, tak by se mi ta závislost na p těžko vyjadřovala). A této funkci g se také říká metrika (popřípadě metrický tenzor nebo Riemannova metrika - aby se to explicitně odlišilo).

Z kontextu se většinou pozná, zda autor myslí metriku d(x,y), která měří vzdálenosti, a nebo metriku g(p), která skalárně násobí vektory v tečném prostoru TpM.

Ta dvojznačnost má jisté opodstatnění, protože metriku d si z metriky g můžeme nabrnkat sami. Minule jsme viděli jak to zaonačit: Riemannova metrika g(p) nám umožňuje v tečném prostoru TpM definovat normu (velikost vektoru) pomocí skalárního součinu a pokud právě změřený tečný vektor "lehce ohneme" exponenciálním zobrazením, můžeme ho použít jako "měřicí tyčku" pro definici vzdálenosti d(p,q) na varietě. Alespoň tedy lokálně - v okolí bodu p - ale to nám stačí. I vzdálenost mezi Prahou a Hradcem se dá v principu změřit třiceticentimetrovým pravítkem.

V prostoročasu to funguje podobně. Pokud je zakřivený, dá se popsat pomocí zmíněných pseudo-Riemannovských variet. Podle Einsteinovy teorie gravitace (obecná relativita) je ta prostoročasová metrika g určena rozložením hmoty a energie. To znamená, že lokální měření délek závisí na tom, kolik je v okolí "hmotoenergie" (jinými slovy - to třiceticentimetrové pravítko není úplně tak rigidní, jak si obvykle představujeme).

Vlastnosti metrického tenzoru g(p) jsou pak klíčové pro určení zakřivení prostoru a tím pádem i jeho geometrie a dynamiky objektů v něm se pohybujících - ale o tom až někdy jindy.

(každá myš, která dorazila až sem, má nárok na 50 gramů ementálu)

+++++++++

Na vydýchání si opět dáme moderní verzi jedné klasické písničky. Tentokrát to bude ústřední melodie z filmu "Čaroděj ze Země Oz" v podání punk rockove skupiny Me First (tady je koncertní verze; originál s Judy Garland naleznete zde). Me First and the Gimme Gimmes: Over the Rainbow.

Předchozí díly Matykání