Matykání: kdo se bojí, nesmí do nekonečné dimenze
Nejprve stručná rekapitulace, co je v nekonečnu nového.
Při náhodné prohlídce doručené pošty hrabě Nikolič zjistí, že mu zvedli jeho nekonečné daně na dvojnásobek, ale vzápětí se rozesměje huronským smíchem, když si uvědomí, že dvakrát nekonečno je stále jen nekonečno. Transfinitní Indukce je konečně provdaná a žije s Houslovým Klíčem poblíž visacího zámku Konopiště. Statkář Hlavsa si omylem pořídil spočetně mnoho krav a pouští se do stavby průtokového ordinálního chléva. Uprostřed vyzdívání triliontého výklenku však čeledín Josef hněvivě odkládá zednickou lžíci a ve stáří alef nula až alef dva odchází ze statku. Hrabě Nikolič se nečekaně vrací z honu a na divanu nalézá povalující se osmičku. Přivolaná služebná si zakryje oči a vydělí ji nulou. Do sousedního vesmíru téměř souběžně vyhřezne Velký Třesk. V lomu hraběte Nikoliče se pomalu rozptyluje zvířený prach.
Na první pohled by se mohlo zdát, že prostory s konečnou dimenzí nám poskytují vše, co běžný vědec potřebuje ke svému životu. Ale s nástupem kvantové mechaniky a dalších moderních disciplin se ukázalo, že na některé objekty (např. posloupnosti či funkce) je výhodné pohlížet jako na vektory s nekonečnou dimenzí, protože to umožňuje využít a rozšířit bohatý aparát lineární algebry. Tato nadstavba, zvaná funkcionální analýza, se pak rozvíjela ruku v ruce s kvantovou fyzikou.
Tak limitní gumáky na nohy a vzhůru do nekonečna!
+++++++++
Prostory posloupností
Asi nejjednodušší způsob, jak si nabrnkat nekonečnou dimenzi je postupně přidávat souřadnice a když je proces úspěšně nastartován, nechat ho běžet samospádem a odejít do kina.
Vezmeme si nějaký jednoduchý vektor a podíváme se na to:
2D: u=(1,1)
3D: u=(1,1,1)
4D: u=(1,1,1,1)
5D: u=(1,1,1,1,1)
...
no a když se vrátíme z kina, máme na stole nekonečně-rozměrný vektor
?D: u=(1,1,1,1,1,1,1,1,1,...)
(tři tečky naznačují, že pokračujeme stále dál a dál)
Z pohledu běžného smrtelníka jsou takové "vektory" nekonečnými posloupnostmi.
Zopakujme si, že vektorový prostor (ve svém nejhrubším modelu - tedy bez automatické převodovky) je v podstatě množinou objektů, které se dají navzájem sčítat a násobit skaláry.
Tyto operace fungují přesně jak očekáváme. Bude-li
u=(1,1,1,1,1,1,1,1,1,...)
v=(1,2,3,4,5,6,7,8,9,...)
pak si lehce spočteme libovolné lineární kombinace
u+v = (2,3,4,5,6,7,8,9,10,...)
u-v = (0,-1,-2,-3,-4,-5,-6,-7,...)
5u = (5,5,5,5,5,5,5,5,...)
3v-2u = (1,4,7,10,13,16,19,...)
Ta základní struktura vektorového prostoru evidentně hladce funguje i s nekonečně mnoha souřadnicemi - přestože jejich zadání je trochu problém, protože jsme prakticky omezeni na příklady, kde se dá najít určitý vzorec chování - např. lineární růst, exponenciální pokles atd. Nicméně, pokud ten vzorec chování (či trend, chcete-li) vyhmátnete, tak si lehce domyslíte, jak se s takovými objekty manipuluje.
U mnoha aplikací ale význam vektorových prostorů tkví v jejich geometrickém příslušenství. Tedy v tom, že jsme schopni měřit délku vektorů (pomocí normy) a úhly mezi nimi (pomocí skalárního součinu). A tady narazíme na problém. Pokud pro definici normy a skalárního součinu zobecníme tradiční eukleidovský přístup, většina vektorů bude mít nekonečnou délku (například ten "jedničkový" u). Proto je nutno velikost jednotlivých členů (tj. složek nekonečných vektorů) nějakým způsobem omezit.
Norma a skalární součin se rozšíří takto:
|| u || = sqrt(u12 + u22 + u32 + ...)
u . v = u1*v1 + u2*v2 + u3*v3 + ...
(v obou případech je tedy výsledkem součet nekonečné řady)
Pro praktické počítání pak používáme prostor posloupností jejichž norma je konečná (tj. součet čtverců dané posloupnosti je konečný). Tomuto prostoru se říká l2 (EL dva) a je pravděpodobně nejjednodušším nekonečně rozměrným prostorem, se kterým se v praxi setkáte (o něco obecnější jsou tzv. lp prostory). Můžete si sami ověřit, že konečné lineární kombinace takových vektorů budou mít stále konečnou normu (plyne to z trojúhelníkové nerovnosti). O skalární součin se strachovat nemusíme, protože jeho velikost je omezena Cauchy-Schwarzovou nerovností.
Proč je prostor l2 nekonečně rozměrný? Protože dimenze je v podstatě počet nezávislých vektorů, které se daného prostoru dají nacpat. Vektory (posloupnosti), které mají všude 0 a pouze na i-té pozici 1, jsou lineárně nezávislé a je jich nekonečně mnoho.
ui = (...,0,0,1,0,0,0,...)
Vektory ui tedy tvoří bázi prostoru l2, stejně jako jejich konečně rozměrné protějšky tvoří bázi eukleidovskch prostorů R^n (pozor ale na značení - ui někdy znamená i-tý vektor, jindy i-tou složku jednoho konkretního vektoru - z kontextu bude většinou jasné, která bije).
Možností, jak nekonečné posloupnosti zkrotit a přiřadit jim konečnou "délku" (tedy z vektorového pohledu normu) je samozřejmě povícero. Další poměrně populární variantou je supremum přes všechny členy. Supremum je v podstatě maximum, jen s tím rozdílem, že ho ta posloupnost (či obecněji množina) nemusí nutně nabývat - např. posloupnost {1-1/n} má supremum 1, přestože se žádný člen 1 nerovná (supremum je nejmenší možná hodnota, která je "nad" celou posloupností/množinou). Prostory se supremovou normou ale nemají odpovídající skalární součin, takže představují o něco chudší systém.
+++++++++
Na počátku této série jsme si řekli, že matematika preferuje uzavřené struktury, tedy takové kdy při provádění algebraických či geometrických operací z dané množiny nevypadnete.
Nekonečně rozměrné prostory mají v tomto ohledu jednu nepříjemnou vlastnost. Dá se z nich (v principu) vykonvergovat ven. Podívejme se, jak k tomuto politováníhodnému nedopatření může dojít.
Uvažujme vektorový prostor p, skládající se z posloupností, které mají pouze konečný počet nenulových členů, tedy např.
u=(1,3,0,0,0,0,...)
v=(0,0,2,0,1,1,8,0,0,0,...)
Nejprve si ověřte, že takto definovaná nestvůra je skutečně vektorový prostor - tj. součet i skalární násobek takových vektorů bude mít stále jen konečný počet nenulových členů.
A teď se podívejme na následující posloupnost vektorů
(je to vlastně posloupnost posloupností)
u1 = (1,0,0,0,0,0...)
u2 = (1,1/2,0,0,0,0,...)
u3 = (1,1/2,1/3,0,0,0...)
u4 = (1,1/2,1/3,1/4,0,0...)
...
každá taková posloupnost má pouze konečně mnoho nenulových elementů a je tedy pravoplatným příslušníkem našeho prostoru p (číslo členské legitimace ?2). Když se na ni ale podíváte podrobněji, zjistíte, že konverguje k posloupnosti
u = (1,1/2,1/3,1/4,1/5,1/6,...)
Ta limitní posloupnost u má všechny členy nenulové, takže už není součástí prostoru p (byť je součástí nějakého "většího" prostoru) a nám se tedy podařilo z něho vykonvergovat ven.
(konvergencí tady samozřejmě myslíme konvergenci ve smyslu normy - v tomto případě je jedno, zda si vezmete tu tradiční a nebo tu supremovou)
un --> u jestliže platí || un - u || --> 0
(tedy lidově řečeno, posloupnost vektorů un konverguje k vektoru u, jestliže se velikost jejich rozdílu blíží nule)
Když si ten limitní vektor odečteme, dostanete n nul a malý "ocásek"
un - u = (0,0,0,...,0,1/n,1/(n+1),1/(n+2),...)
jehož norma se blíží k nule (se zvyšujícím se n). To je lépe vidět pro tu supremovou normu, která je 1/n (to je nejmenší číslo ležící nad celou posloupností). Pro tu standardní byste se museli opřít o fakt, že součet ?1/n2 je konečný, takže na ten "ocásek" zbývá (s rostoucím n) stále méně a méně.
U konečně rozměrných prostorů nám taková habaďůra neprojde. Pokud máte posloupnost vektorů Vn, které k něčemu konvergují, pak limita V leží nutně v tom samém prostoru (viz ilustrační obrázek).
Tady byste mohli namítnout, že vykonvergovat se dá i v 1D, tedy přímo na reálné přímce. Například z otevřeného intervalu (0,1) lehce vykonvergujete posloupností {1/n} (jejíž členy jsou součástí intervalu, zatímco limita 0 už ne). Ten interval ale sám o sobě není vektorovým prostorem (jako byl prostor p).
Protože limita je poměrně důležitým pojmem, matematika preferuje vektorové prostory, ze kterých se vykonvergovat nedá. Takovým říká "úplné" (angl. complete spaces).
A na závěr sekce malou technickou: Protože operovat nějakou limitou, která je de facto mimo daný prostor není úplně košer, v definici úplných prostorů se používají tzv. cauchyovské posloupnosti, jejichž "sbíhavost" je definována pomocí jejich vlastní vnitřní struktury (bez odkazu na případnou limitu, která si může trůnit bůhví kde). Lidově: cauchyovská posloupnost vypadá, jakože se k něčemu blíží, ale protože její limitu nevidíme, nejsme schopni rozhodnout, zda je konvergentní (definice konvergence totiž tu limitu předpokládá). Demokraticky: posloupnost je cauchyovská, pokud pro danou toleranci ?>0 existuje index n tak, že všechny členy posloupnosti od tohoto indexu dál se od sebe neliší více než o ?. Pokud je každá cauchyovská posloupnost konvergentní, prostor je úplný a nedá se z něho vykonvergovat ven. Opět si představte ten 1D příklad: otevřený interval (0,1) není úplný (coby metrický prostor***), protože posloupnost {1/n} (která je jeho součástí) konverguje k něčemu, co je mimo něj (nula). Z pohledu intervalu (0,1) je posloupnost {1/n} cauchyovská, ale není konvergentní (číslo nula v něm nikdo nezná). Z pohledu uzavřeného intervalu [0,1] by konvergentní byla (z intervalu [0,1] nevykonvergujete ani náhodou - proto je úplným prostorem).
***(metrický prostor je struktura, kde nás zajímá pouze měření vzdáleností a lineární strukturu vzal čert - vektorový prostor je jejím speciálním příkladem, protože vzdálenost d(u,v) můžeme odvodit z normy)
+++++++++
Prostory funkcí
Na funkce se většinou díváme jako na něco, co na vektorovém prostoru operuje (do funkce vhodíte vektor jako argument a na výstupu vám vypadne jiný vektor jako funkční hodnota). Obrazně řečeno: pokud si vektorový prostor představíme jako zemědělské pole, pak funkce je spíš určitý typ nástroje, něco jako pluh či podmítač, než kus hroudy. Ale v průběhu 20. století se ukázalo, že i na celou množinu těch nástrojů (tedy funkcí s určitými vlastnostmi) se můžeme dívat jako na abstraktní vektorový prostor. Koneckonců, i funkce můžeme sčítat mezi sebou či násobit skalárem (měl by to zvládnout každý středoškolák). Například je-li f(x)=sin(x) a g(x)=exp(x), pak f+g je funkce definovaná předpisem
f(x)+g(x) = sin(x)+exp(x)
Obdobně se definuje skalární násobek:
3f(x) = 3 sin(x)
Vektorový prostor je pak tvořen množinou všech funkcí na nějakém intervalu s určitými vlastnostmi (např. pouze funkce spojité, integrovatelné atd), aby nebyl příliš divoký. Při definici vektorového prostoru funkcí pak musíte jen ověřit, že při provádění součtu a skalárního násobku ty vlastnosti neztratíte.
Například množina všech kvadratických funkcí (tvaru ax2+bx+c) je vektorovým prostorem, protože sčítáním kvadratických funkcí dostanete zase funkci kvadratickou a podobně pro násobek. Ale pozor, množina kvadratických funkcí s nenulovým kvadratickým členem (a?0) už vektorovým prostorem není. Uvažujme f(x)=x2 a g(x)=-x2. Jejich součtem f+g je konstantní nula (a ta má ten kvadratický koeficient nulový - respektive je má nulové všechny).
+++++++++
Jakmile máte vektorový prostor funkcí pevně ukotvený, můžete na něm začít operovat pomocí speciálních funkcí, kterým se říká operátory - aby se to nepletlo s funkcemi, které tvoří "bodíky" našeho vektorového prostoru a které vhazujeme na vstup. Pokud má příslušný operátor na výstupu skalár pak mu říkáme funkcionál - odtud i název oboru funkcionální analýza.
Operátory (na vektorových prostorech) hrají centrální úlohu v matematickém formalismu kvantové mechaniky (např. polohový operátor nebo operátor hybnosti). Abychom se ale příliš nezamotali do kvantové provázanosti, podíváme se pro ilustraci na dva jednoduché funkcionály P a Q (můžete si je představit jako definované na prostoru spojitých funkcí na intervalu (0,1)).
Oba představují jakousi pomyslnou skříňku, kam vhodíme příslušnou funkci z našeho prostoru a na výstupu nám vypadne skalár (zde reálné číslo). Ten první funguje tak, že operátor nám prostě vyhodí hodnotu funkce v nějakém pevném bodě - řekněme v nule.
P(f) = f(0)
Ten druhý nám vyhodí plochu pod grafem funkce na zvoleném intervalu (meze integrálu jsou tím intervalem určené)
Q(f) = ?f ... což je zkratka pro ?f(x)dx
Můžete si sami ověřit, že oba operátory jsou lineární, tedy splňují
jednak L(f+g) = L(f) + L(g) a druhak L(af)=aL(f)
(pro každou dvojici funkcí f a g a pro každý skalár a)
Jakmile máte své operátory a funkcionály definované, můžete začít zkoumat jejich vlastnosti (kde nabývají extrému, jak rychle se mění, v kolik hodin večeří atd). Jen musíte mít na paměti, že se pohybujete na prostoru funkcí - což je podstatně zrádnější bažina než Alenčin storozměrný eukleidovský prostor. Na hledání maxima funkcionálů budete například potřebovat speciální kalkulus variací, zatímco u obyčejných funkcí vám (na trojku do indexu) stačilo položit derivaci rovnou nule.
+++++++++
Část té zrádnosti spočívá v tom, že i prostory funkcí jsou obecně nekonečně dimenzionální. Ale zatímco u posloupností to bylo vidět triviálně (vektory měly "už od pohledu" nekonečně mnoho složek), tady si to budeme muset trochu rozmyslet.
Začneme tím, že dvě funkce z nějakého funkčního prostoru (definovaného na intervalu I) se rovnají, jestliže se rovnají jejich funkční hodnoty pro všechna x z intervalu I:
f = g tehdy a jen tehdy, pokud f(x)=g(x) pro všechna x ? I
To znamená, že např. funkce 1+x a x2 jsou dva různé "vektory", přestože rovnice 1+x = x2 má dvě konkrétní řešení. Ale to na rovnost ve smyslu funkcí nestačí. Tam by se to muselo rovnat sakum pikum. Ta řešení kvadratické rovnice nám pouze naznačují, že grafy daných funkcí se protínají (a to není to samé co jejich rovnost).
Vyzbrojeni touto úvahou si rozmyslíme, že množina všech mocnin {1,x,x2,x3,...} je lineárně nezávislá. Zhruba řečeno to funguje takto: každá další mocnina, kterou přidáváte, je nezávislá (coby "vektor") na těch předchozích (nedá se z nich vytvořit kombinací). Představme si třeba (pro spor), že funkce x3 by se dala netriviálně vyjádřit pomocí předchozích mocnin.
x3 = a0 + a1*x + a2*x2 pro všechna x ? I
To ale opět není možné, protože takto vzniklá kubická rovnice může mít maximálně tři kořeny - nemůže tedy platit pro všechna x ? I. A pro vyšší mocniny to platí jakbysmet.
To znamená, že do našeho prostoru se dá umístit libovolný počet nezávislých vektorů (každá mocnina zde reprezentuje jeden vektor) a z toho vyplývá, že jeho dimenze (maximální počet nezávislých vektorů) musí být nekonečno.
+++++++++
Jakmile se nám z množiny všech funkcí podařilo vyseknout část, která se chová jako ctihodný vektorový prostor, můžeme na něm zavést normu (někdy i skalární součin) a začít páchat geometrická kouzla (jak "velikost" funkce, tak "úhel" mezi dvěma funkcemi jsou teď ovšem jen abstraktní analogie - nepředstavujte si ho jako úhel pod kterým se protínají jejich grafy - ty se koneckonců protínat vůbec nemusí).
Abychom se neztratili v džungli Lebesgueových či Sobolevových prostorů, uděláme to čistě intuitivně a budeme předpokládat, že všechny níže popsané integrály existují a dají se vyčíslit (jsou spočítané přes konkrétní interval na kterém je funkční prostor definován).
Norma funkce f se dá definovat takto: || f ||2 = ? f2
a skalární součin pak funguje takto: f.g = ? f.g
Prostoru funkcí s konečnou normou se říká L2.
(v komplexním případě je druhý člen v tom součinu komplexně sdružený)
Když si ten vzoreček pro skalární součin porovnáte s tím posloupnostním (z předchozí sekce), zjistíte, že mají prakticky stejnou strukturu. Oba představují součet součinů přes všechny komponenty daného "vektoru". U posloupností je to diskrétní součet (přes spočetně mnoho komponent), zatímco u funkcí je to spojitý součet (integrál) a těch komponent (bodů intervalu) je nespočetně mnoho.
To, že jsme i v nekonečné dimenzi schopni definovat geometrické nástroje (normu a skalární součin) znamená, že se můžeme opřít o celý aparát lineární algebry a zkoumat jemnější geometrické vlastnosti těchto prostorů. Například speciální projekce na nejrůznější podprostory (jako když z 3D prostoru promítáte do 2D roviny). V sekci Jauvajs se podíváme na jednu z nejznámějších - Fourierovy řady.
+++++++++
Dáte si Hilberta nebo Banacha?
Při četbě matematických textů se zhusta stane, že čtenář narazí na nějaký technický termín a neznaje jeho významu, otráveně článek odloží. Při tom spousta termínů jsou ve své podstatě jednoduché pojmy, pouze zahalené do blyštivého hávu abstrakce. A aby to bylo lautr sychr, že se čtenář lekne, obvykle jsou tito strašáci pojmenovaní po nějakém matematickém géniovi, zamračeně vyhazujícím nevinné studenty od zkoušek. K takovým patří Hilbertův, resp. Banachův prostor.
V první aproximaci si je lze představit docela jednoduše.
Především jsou to oba vektorové prostory (ať s konečnou či nekonečnou dimenzí), s tím, že na Banachově prostoru lze definovat pouze normu vektoru, zatímco na Hilbertově máme k dispozici i skalární součin.
Pokud tedy v textu narazíte na Hilbertův prostor, klidně si představte R2 se skalárním součinem, zatímco v případě Banachova prostoru se v tom modelovém R2 budete muset spoléhat jen na normu (tvařte se, že o skalárním součinu nic nevíte). Samozřejmě tím přijdete o některé fajnovosti funkcionální analýzy, ale troufám si říci, že většinu článků budete moci v klidu dočíst až do konce.
Zatímco normu si ze skalárního součinu odvodíme triviálně (každý Hilbertův prostor je tedy automaticky Banachův), obráceně je to komplikovanější (ne každý Banachův prostor je Hilbertův). Skalární součin se dá z normy odvodit pomocí polarizační identity pouze pokud norma splňuje rovnoběžníkové pravidlo:
(R) || u+v ||2 + || u-v ||2 = 2 || u ||2 + 2 || v ||2
To nám ukazuje, kde leží hraniční čára mezi oběma typy prostorů.
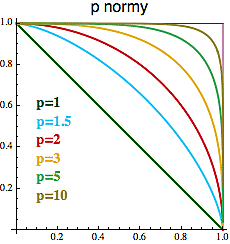
Jako příklad si vezměme tradiční 2D rovinu a na ní si pro každé reálné číslo p>1 definujeme tzv. p-normu vektoru u=(x,y) vztahem
|| u ||^p = |x|^p + |y|^p
(pro p=2 dostanete obvyklou eukleidovskou normu)
Takto definovaná funkce na vektorech splňuje podmínky normy (pro každé p>1), takže rovinu můžeme proměnit v Banachův prostor nekonečně mnoha způsoby. Abychom si tu p-normu mohli nějak lidsky představit, podívejme se na kousek jednotkových kružnic v těchto normách - tj. na množinu vektorů u=(x,y) splňujících x^p + y^p=1 (viz obrázek).
To že pro p?2 tato norma nesplňuje rovnoběžníkové pravidlo se dá nahlédnout tak, že si vezmeme dva vektory: u=(1,0) a v=(0,1) a obě strany rovnice (R) si vyčíslíme. Naopak pro p=2 to rovnoběžníkové pravidlo plyne např. z věty kosínové (example 6).
Zajímavé je, že když si představíte ty "jednotkové kružnice" pro větší a větší hodnoty p, tak zjistíte, že v limitě se blíží tomu hraničnímu čtverci. Ten de facto představuje "jednotkovou kružnici" ve výše zmíněné supremové normě, kterou pro 2D vektor u=(x,y) můžeme zapsat pomocí maxima:
|| u || = max(|x|,|y|)
Ta p-norma se dá samozřejmě zavést i v nekonečné dimenzi: v případě posloupností dostaneme tzv. lp prostory, zatímco pro funkce jim říkáme Lp prostory. Všechno dohromady jsou to Banachovy prostory (mají normu), ale pouze pro p=2 jsou i prostory Hilbertovými. A protože ta supremová (maximová) norma je vlastně limitním případem p-norem (pro p=?), jak jsme viděli na obrázku, vektorovým prostorům opatřeným touto normou se říká l? (pro posloupnosti) a L? (pro funkce).
+++++++++
A ještě malá technická douška.
Protože jak Hilbertův, tak Banachův prostor může být nekonečně rozměrný, musíme ještě zaručit, že se z těchto prostorů nedá vykonvergovat ven (do žitného pole). V obou případech tedy vyžadujeme, aby příslušný vektorový prostor byl úplný.
V první sekci jsme viděli, jak lehce se dá vykonvergovat z prostoru posloupností, tak se teď podíváme, jak se dá vykonvergovat z prostoru funkcí.
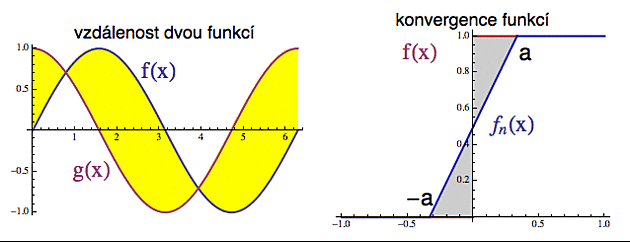
Vezmeme si prostor spojitých funkcí na intervalu (-1,1) a na něm si definujeme posloupnost funkcí fn takto (viz obrázek vpravo). Pro každé n si spojíme přímkou body -a=(-1/n,0) a a=(1/n,1) s tím, že nalevo tu funkci fn dodefinujeme nulou a napravo jedničkou (modrá funkce v pravém obrázku).
Abychom se mohli bavit o konvergenci, definujeme si normu funkce pomocí integrálu z absolutní hodnoty (ta mimochodem odpovídá prostoru L1)
|| f || = ? | f |
a to znamená, že vzdálenost mezi dvěma funkcemi je určena plochou mezi jejich grafy (žlutá partie ma obrázku vlevo).
Teď se přesvědčíme, že funkce fn v této normě konvergují k nespojité funkci f,
kde f(x)=0 pro x?(-1,0) a f(x)=1 pro x?(0,1)
(na obrázku vpravo je f vyznačena červeně - byť je částečně zakryta)
Norma rozdílu || fn - f || je plocha vystínovaných trojúhelníků vpravo a ta se (pro zvětšující se n) "zužuje" k nule. Spojité funkce fn tedy konvergují k funkci f, která spojitá není (podobný příklad zde).
Opět vidíme, že v nekonečné dimenzi musíme být opatrní, aby nám vektory v limitě "nevytekly" z prostoru. Proto mají Banachovy i Hilbertovy prostory v sobě zabudovanou podmínku úplnosti.
+++++++++
Sekce jauvajs: Fourierovy řady
(jen pro mimořádně otrlé povahy)
Jedním z důvodů, proč se vyplatí pohlížet na funkce prizmatem vektorových prostorů je možnost rozkládat funkce na elementární (bázové) komponenty.
Všichni známe ze střední školy klasický obrázek (vpravo), kde se nějaký obecný vektor u rozloží na složky působící ve směru bázových vektorů v a w, ať už jsou to vektory přizpůsobené danému problému (např. vektor působící kolmo na podložku versus vektor působící podélně) anebo ty standardní ve směru souřadných os.
Pokud jsou vektory v a w kolmé, můžeme rozklad zapsat explicitně
u = a v + b w = (u,v) v + (u,w) w
kde koeficienty rozkladu a,b není nutno pracně počítat rovnicemi, ale získají se zadarmo z naznačeného skalárního součinu.
Nabízí se tedy otázka, zda by se i funkce nedaly rozložit podobným způsobem na nějaké základní (bázové) elementy - když už se na ně tedy díváme jako na prvky abstraktního vektorového prostoru.
Asi nejznámějším příkladem takového rozkladu jsou tzv. Fourierovy řady.
Vezměme si funkce definované na intervalu (-?,?) se skalárním součinem definovaným pomocí integrálu přes tento interval (tedy od -? do ?).
(f,g) = ? f.g
Abychom se nerozptylovali detaily, různé technické předpoklady a normalizační konstanty zde potlačím a budeme předpokládat, že funkce jsou dostatečně slušně vychované, aby se ty integrály daly spočítat (podrobnosti i konstanty najdete anglicky here a česky tady). Jenom poznamenám, že na rozkládané funkce se velmi často díváme jako na funkce periodické (mimo ten základní interval je rozšíříme prostým opakováním).
Nejprve budeme potřebovat dostatečně bohatý systém bázových funkcí, které jsou navzájem pravoúhlé ve smyslu skalárního součinu - tedy pro každý pár bude platit (f,g)=0. V průběhu 19. století se ukázalo, že takovým systémem je množina sínů a kosínů s celočíselnými násobky základní frekvence (ke kterým ještě přidáme konstantní funkci f(x)=1):
sin(x), sin(2x), sin(3x), sin(4x), sin(5x), ...
cos(x), cos(2x), cos(3x), cos(4x), cos(5x), ...
Můžete si sami zkusit (integrováním od -? do ?), že tyto bázové funkce jsou skutečně navzájem "kolmé", tj. jejich skalární součiny se vynulují
(1,sin(x)) = ?sin(x)dx = 0
(1,cos(x))= ?cos(x)dx = 0
(sin(x),cos(x))= ?sin(x)*cos(x)dx = 0
(sin(x),sin(2x))= ?sin(x)*sin(2x)dx = 0 ... atd
S trochou práce se pak dá ukázat, že tyto vektory (patřičně normalizované funkce) tvoří ortonormální bázi příslušného vektorového prostoru a každou další funkci tedy můžeme rozložit přesně jako ten 2D vektor u na začátku sekce
f(x) = a0*1 + a1*sin(x) + b1*cos(x) + a2*sin(2x) + b2*cos(2x) +...
kde koeficienty se spočítají úplně stejně jako ve 2D, tedy pomocí skalárního součinu rozkládané funkce f(x) a příslušných bázových vektorů (funkcí)
a0 = (f(x),1) = ?f(x)dx
a1 = (f(x),sin(x)) = ?f(x)*sin(x)dx
a2 = (f(x),sin(2x)) = ?f(x)*sin(2x)dx
...
b1 = (f(x),cos(x)) = ?f(x)*cos(x)dx
b2 = (f(x),cos(2x)) = ?f(x)*cos(2x)dx
...
Tímto způsobem se každá funkce s periodou 2? dá rozložit na nekonečný součet sínů a kosínů, nesoucí hrdé jméno Fourierova řada funkce f.
Pokud si z té Fourierovy řady vezmete jen několik prvních členů (a ruku na srdce, kdo by se chtěl tahat s celým nekonečným ánsámblem), tak získáte poměrně solidní aproximaci funkce f(x) (de facto průmět do podprostoru určeného příslušnými ortogonálními funkcemi - stejně jako byste si z toho úvodního 2D rozvoje vzali pouze jeden člen).
Úspěch Fourierova aparátu nás přivádí k otázce, zda by se nedaly najít ortogonální množiny polynomů, do kterých bychom mohli dané funkce podobným způsobem promítat. To je problém o něco komplikovanější a existuje několik typů vzájemně "kolmých" polynomů, které k tomuto účelu můžete použít (k nejznámějším patří Legendreovy, popř. Čebyševovy polynomy).
+++++++++
Ze školy si možná vzpomínáte na Taylorovy řady, které rozloží danou funkci na nekonečnou lineární kombinaci mocnin. To je sice podobná myšlenka - ale implementace je zcela jiná.
Taylorovy řady jako koeficienty nepoužívají skalární součiny dané funkce s nějakými bázovými vektory, ale vyšší derivace v předem zadaném bodě (časem se k nim vrátím).
To má jeden důležitý praktický důsledek. Pokud funkci mimo bod rozvoje "trochu" pozměníte, Taylorova řada to většinou nepozná (bude stále stejná), protože derivace v tom bodě se nezměnily. Fourierova řada by to poznala - protože skalární součiny jsou definované integrálem přes celý interval a tam se to projeví (pokud je změna uvnitř intervalu). Taylor se tedy snaží aproximovat chování funkce v nejbližším okolí bodu rozvoje, zatímco Fourier na celém intervalu.
Můžete si třeba vzít exponencielu na intervalu (-1,1), promítnout ji do podprostoru generovaného funkcemi (1,x,x2), respektive příslušnými Legendreovými polynomy, a takto vzniklý kvadratický polynom p(x) (jehož koeficienty získáte ze skalárních součinů) porovnat s Taylorovým polynomem druhého řádu t(x). Budou se trochu odlišovat. Ten první vyjde p(x)=0.54x2+1.1x+0.996, zatímco ten druhý t(x)=0.5x2+x+1 (podrobnosti zde a zde).
+++++++++
V roce 1980 natočil britský režisér Peter Collinson komorní drama The Earthling (Pozemšťan), jehož tíhu prakticky beze zbytku nesou dva herci z opačného pólu věkového spektra. Devítiletý Ricky Schroder a oproti němu zkušený William Holden ve své předposlední filmové roli. K jednoznačným kladům tohoto zajímavého snímku patří i povedená a skvěle zazpívaná titulní písnička. Maureen McGovern: Halfway Home.
Předchozí díly Matykání
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
Jan Řeháček
Co rok dal

Začátek nového roku je tradičně příležitostí k ohlédnutí za rokem starým, takže jsem prohrábl archív a vylovil z něho pár fotografií z našeho parku, které si nenalezly cestu do některého z předchozích tématických blogů.
Jan Řeháček
Politické školení mužstva: Pyšná princezna

Roto končit! Pozor! (vejde útvarový politruk) Soudruzi vojáci, kapitál se potácí. Ale sám se nám na smetiště dějin nevypotácí. My mu musíme co, soudruzi? No? Nikdo? No, my mu musíme pomoci, vy hlavy hovězí!
Jan Řeháček
Ten podzim se nám hezky vybarvil

Každý podzim je v našem parku trochu jiný. Stromy, které by loni přešminkovaly i šestnáctku před prvním rande, jsou letos pobledlé jako Rusalka. A ty, které se zprvu barevně upejpaly, se najednou utrhly z řetězu. Jak řezníkův pes.
Jan Řeháček
Paroháčů je letos dost

Srnka je v našem parku jako houska na krámě. Zato setkání s jelenem si člověk musí považovat. Letos jsem ale náhodou objevil, kde se srocují: na záložním travnatém parkovišti, kterému se říká Gil's Hill, těsně před západem slunce.
Jan Řeháček
Chřadnoucí prales - pod vodou i nad ní

O korálovém útesu se říká, že je to "dešťový prales" oceánu. Biodiversita, kterou reprezentuje je ohromující. Totéž platí i o jeho suchozemském ekvivalentu. Bohužel, oba ekologické systémy se dostávají na seznam ohrožených druhů.
Jan Řeháček
Letní kvítí

Primární sezónou květů je sice jaro, ale ani léto není v našem parku z pohledu barev úplná nuda. Tady je malá fotovonička složená z příspěvků místní flory. Aneb kdo nekvete s námi, kvete proti nám.
Jan Řeháček
Plody léta

Léto je časem zrání a ani v našem parku tomu není jinak. Zajímavé plody nabízí říše rostlinná i živočišná. Tady je malý průřez letošní nabídkou: asijské maliny, kuriózní houby a malí mývalové. Ceny jsou mírné: léto létá zdarma.
Jan Řeháček
Kvetoucí fuga (Beethoven)

V Beethovenově Misse Solemnis nalezneme spoustu skrytých drahokamů, které zde leží prakticky nepovšimnuty, protože celková hudební struktura této Mše je na první poslech naprosto neprůstřelná. Jedním z nich je fuga v závěru Creda.
Jan Řeháček
Sovy a supi

V našem parku také poletuje spousta zajímavých ptáků. Tak jsem jich pár vyfotil. Sovy jsou sice nočními živočichy, ale na jaře se občas dají zastihnout i za denního světla. A za pár šupů k nim přihodím ještě pár supů. Ať nežeru.
Jan Řeháček
Vlčí západy

Při procházkách naším parkem občas fotím západy slunce z vyvýšeného travnatého parkoviště zvaného Gil's Hill. Říkám jim Vlčí západy. Jednak proto, že mají zhusta barvu vlčích máků a jednak proto, že náš park se jmenuje Vlčí past.
Jan Řeháček
Za devatero fotkami: Malebné peklo

Já to tušil, že jednou skončím v pekle. Jen jsem si představoval, že vstup bude mít z nějaké islandské sopky. Houbeles! Jeho vchod se nalézá poblíž vesničky Medkovy Kopce nedaleko Hlinska. "Lasciate ogne speranza, voi ch'intrate".
Jan Řeháček
Sedm divů jara

Po dlouhém barevném půstu zimní šedi působí návrat jarní kavalerie jako zjevení. V našem parku v tomto období kvete několik dřevin, s jejichž uměleckými kreacemi bych vás v tomto blogu rád seznámil. Matička příroda dokáže kouzlit.
Jan Řeháček
strž

V dnešním pokračování poetického cyklu "Bez básně a Hany" se nedozvíme jakou krevní skupinu mají nejraději novozélandští upíři a zda je tuna pampeliškového chmýří těžší než sbírka maturitních příkladů z matematiky.
Jan Řeháček
Devět zastavení času

Příroda se mění pomalu, ale jistě. Den ze dne nic nepostřehnete, ale když se na známá místa vrátíte za pár týdnů, naleznete desítky drobných změn. Tak jsem se na třech místech našeho parku devětkrát zastavil, abych je zachytil.
Jan Řeháček
Cesta do hlubin duše (Beethoven)

Lidská duše je odvěkou hádankou, na které si vylámaly zuby celé generace psychologů, teologů a filosofů. Tajuplný komplex uvnitř každého z nás. Pro mne je definicí lidské duše Beethovenův 14. smyčcový kvartet cis moll, op. 131.
| předchozí | 1 2 3 4 5 6 7 ... | další |
- Počet článků 402
- Celková karma 19,53
- Průměrná čtenost 920x