Matykání: kruhová inverze - brána do hyperbolické geometrie

Jedním z klasických geometrických zobrazení je kruhová inverze. Moderní počítačová technika ji sice pomalu vytlačuje ze školních osnov, ale pro studium hyperbolické geometrie má stále zásadní význam. Zejména v komplexní rovině.

Symetrie je báječná věc.

Pokud víte, že Petr je zrcadlovým obrazem Pavla, kterého dobře znáte, pak už nemusíte vynakládat prakticky žádný čas na studium Petrových vlastností, protože si je lehce odvodíte z vlastností Pavlových.

I v matematice hraje zrcadlení (konkretně zrcadlení v přímce) důležitou úlohu. Zrcadlový obraz je (až na prohozenou orientaci) praktický totožný s originálem, talže spoustu geometrických úvah a konstrukcí lze jeho prostřednictvím podstatně zjednodušit.

A protože přímka je v podstatě kružnice s nekonečným poloměrem, nabízí se otázka, jak by se mělo definovat zrcadlení v běžné kružnici (tj. s konečným poloměrem). Výsledkem tohoto snažení se stala kruhová inverze - v 19. století jeden z nejpopulárnějších geometrických nástrojů. Lord Kelvin ji aplikoval již ve věku 21 let na některé problémy v elektrostatice.

V moderní matematice se kruhová inverze stala součástí obecnějších geometrických transformací, kterým říkáme Möbiovy transformace. Ty představují nejen standardní nástroj analytických konstrukcí v komplexní rovině, ale v jistém smyslu jsou i páteří Lorentzových transformací ve speciální teorii relativity.

Jak za chvíli uvidíme, kruhové inverze mají se zrcadlením v přímce mnoho styčných bodů. Liší se od nich především tím, že deformují vzdálenosti a tedy obecně i tvary (krásné ilustrace naleznete tady).

Známé ruské úsloví "Nevrč brachu na zrcadlo, máš-li hubu křivou" bychom tedy v matematice mohli pozměnit na "Nevrč brachu na hubu, máš-li křivé zrcadlo".

+++++++++

Kruhová inverze

Na to, jak je toto zobrazení užitečné, je definováno poměrně jednoduše.

Vezmeme si kružnici K (budeme jí říkat řídící kružnice) se středem v bodě O a s poloměrem r a pro každý bod P v rovině definujeme jeho obraz (kruhovou inverzi I) jako bod P', který leží na stejném středovém paprsku (polopřímce) OP a jeho vzdálenost od středu O splňuje rovnici

(+)  OP*OP' = r2

(rozmyslete si, že takový bod je určen jednoznačně)

Pak říkáme, že inverze I zobrazuje P na P'

I: P --> P'

Aby byl součin dvou čísel roven r2, musí být buď obě čísla OP a OP' rovna r nebo je jedno nich větší než r a to druhé menší anebo naopak.

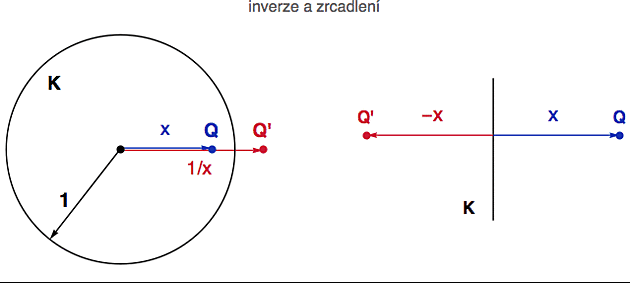
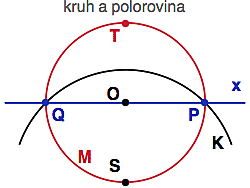
To znamená, že body na řídící kružnici K se zobrazují samy na sebe (říkáme jim samodružné body), body z jejího vnitřku se zobrazují ven a body zvnějšku dovnitř. Abychom mohli s inverzí pracovat v celé rovině, definujeme obraz středu jako nekonečno: O'=? a naopak, nekonečno zobrazíme do středu: ?' = O. Z obrázku vpravo je jasné proč. Jak se s bodem P přibližujeme ke středu O, jeho obraz P' musí nutně odeběhnout do nekonečna, aby stále platila definiční rovnost (+).

Z této rovnice je také patrné, že inverzní zobrazení k I je ta samá kruhová inverze. Provedeme-li ji dvakrát, dostaneme identitu:

I(I(P)) = P pro každý bod P

Kruhová inverze tedy funguje podobně jako reciprocita čísel: 2 a 1/2 jsou dvě navzájem reciproká čísla, stejně jako P a P' jsou dva navzájem inverzní body (vzhledem ke kružnici K).

Abychom si pro inverzi mohli vypěstovat nějakou intuici, představme si pro začátek jednotkovou kružnici. To není problém, délkové jednotky si můžeme vždy zvolit tak, že r=1. Pak je na každém středovém paprsku ta inverze definována přesně jako reciprocita čísel, tj. bod ve vzdálenosti 1/2 se zobrazí na bod ve vzdálenosti 2, bod ve vzdálenosti 3 se zobrazí na bod ve vzdálenosti 1/3, bod ve vzdálenosti 5/7 se zobrazí na bod ve vzdálenosti 7/5 atd.

Podívejme se teď na zajímavou analogii mezi zrcadlením a inverzí. Všimněte si, že zatímco kruhová inverze se opírá o inverzi (reciproké elementy) vzhledem k násobení, přímkové zrcadlení (vpravo) se opírá o inverzi (opačné elementy) vzhledem k operaci sčítání.

Konkretně bod ve vzdálenosti x od řídící přímky se při zrcadlení zobrazí na bod ve vzdálenosti -x, zatímco při inverzi se bod ve vzdálenosti x od středu řídící kružnice zobrazí na bod ve vzdálenosti 1/x. To, co mají obě zobrazení společné je to, že řídící přímka/kružnice se zobrazuje sama na sebe a že dvě oblasti roviny, které ta řídící přímka/kružnice odděluje se zobrazují jedna na druhou.

Na zrcadlení tedy můžeme pohlížet jako na jakýsi limitní případ kruhové inverze, kdy nám poloměr řídící kružnice vzrostl nade všechny meze (stal se nekonečnem). A skutečně si můžete ověřit, že pro velké poloměry r se inverze v blízkosti řídící kružnice chová plus mínus jako zrcadlení. Pokud byste byli plošníci žijící poblíž velké řídící kružnice, tak byste jen stěží rozlišili mezi zrcadlením a inverzí.

Podívejme se na to. Místo abychom zvětšovali poloměr k nekonečnu, zafixujeme si ho jako r=1 a bod P budeme přibližovat ke kružnici K. Jeho vzdálenost od K si označíme x, takže jeho vzdálenost od středu O bude 1-x. Obraz P' bude ležet na stejném paprsku ve vzdálenosti 1/(1-x) což je pro malá x přibližně rovno 1+x (to plyne ze součtu geometrické řady zanedbáním členů vyšších řádů). To znamená, že z pohledu plošníků je bod P' na druhé straně hraniční kružnice (která lokálně vypadá jako kousek přímky) a to zhruba ve stejné vzdálenosti od poloměru r=1.

Úhly ovšem obě zobrazení zachovávají přesně (až na orientaci). Tedy dvě křivky protínající se pod úhlem ? se zobrazí na křivky protínající se pod tím samým úhlem (v absolutní hodnotě).

To je u zrcadlení zřejmé a u inverze se to musí dokázat. Díky této vlastnosti (konformita) se při zobrazování objektů zachovávají jejich geometrické vlastnosti (z deformací délek nemusíme být smutní, protože ty se vždy dají zakamuflovat vhodnou změnou metriky).

+++++++++

Teď když víme, jak se chovají jednotlivé body, podívejme se, jak se při zobrazení chovají kružnice - a v to počítám i přímky, tj. kružnice s nekonečným poloměrem (angličtina, aby to nemusela stále připomínat, na to má bezvadnou vychytávku: cline tedy něco jako křímka).

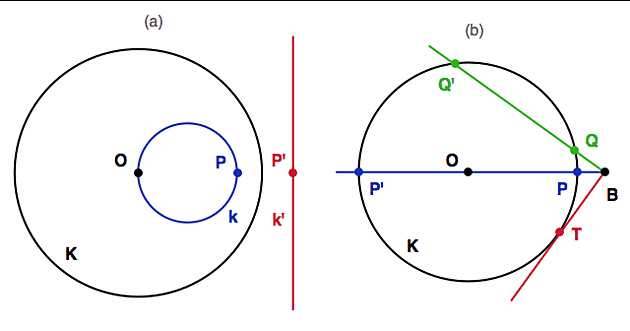
Je fundamentální vlastností inverze, že kružnice se zobrazují na kružnice (i když dokázat to také není úplně triviální). Popřípadě na přímky, pokud zobrazovaná kružnice prochází středem inverze (ten se totiž vždy zobrazí na nekonečno a jediná kružnice, která má šanci se do nekonečna podívat je přímka). Na dalším obrázku vlevo je ilustrační příklad. Řídící kružnice je v černém, zatímco kružnice k a její obraz, přímka k', jsou v červenomodrém.

Abyste to dostali "do ruky", doporučuji pohrát si s touto interaktivní aplikací, kde si pomocí modrých bodů můžete hýbat jak s řídící kružnicí, tak s kružnicí k a v rámečku pak vidíte, jak se chová obraz k'.

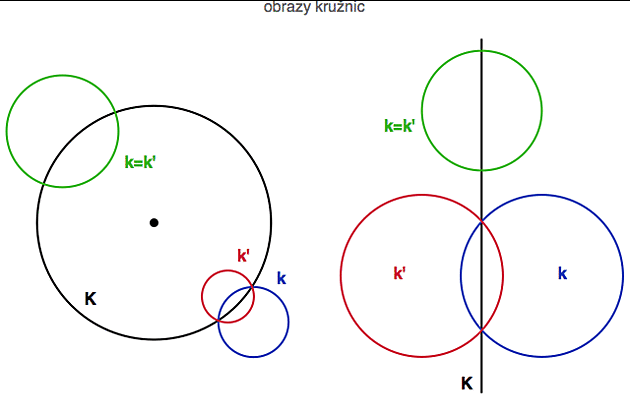
Když budete na levém obrázku tu modrou kružnici posunovat opatrně doprava, v jistém okamžiku se ta kružnice zobrazí sama na sebe. V tom případě říkáme, že kružnice k je vůči inverzi invariantní. Dalším fundamentálním faktem inverzní geometrie je, že kružnice jsou invariantní (vůči inverzi) právě tehdy jsou-li kolmé k řídící přímce (tj. příslušné tečny se protínají v pravém úhlu).

To vyplývá z klasické sečno-tečnové věty, která říká (předchozí obrázek vpravo), že pro každou sečnu kružnice K je součin BP*BP' či BQ*BQ' roven čtverci BT2. Pak už jen stačí si uvědomit, že pokud jsou dvě kružnice pravoúhlé, pak je poloměr jedné z nich tečnou ke druhé v bodě průsečíku T. Zmíněný součin BP*BP'  se zove mocnost bodu ke kružnici a v klasické geometrii patřil k důležitým nástrojům (angl. power of a point). Např. radikální osa dvou kružnic byla množina všech bodů, které měly stejnou mocnost vzhledem ke dvěma kružnicím. Množině všech kružnic se stejnou radikální osou se pak říkalo koaxiální systém (v příští sekci se s jedním seznámíme).

Tady je pro ilustraci té kolmosti ještě jeden obrázek.

Soustřeďme se opět na analogii zrcadlení a inverze. Pokud není kružnice kolmá na řídící kružnici či přímku, má svůj vlastní obraz. Pokud kolmá je (v zeleném), zobrazí se sama na sebe (je tedy invariantní). Přesněji, její vnitřní oblouk se zobrazí na vnější a naopak.

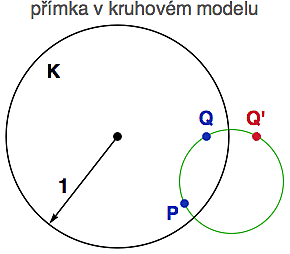
To, že invariantní kružnice jsou kolmé na tu řídící nám umožní hledat přímky v Poincarého kruhovém modelu hyperbolické geometrie. Vezměme si jednotkovou kružnici K a dva body P a Q uvnitř. Jak najít hyperbolickou přímku tyto dva body spojující, tj. jak najít kružnici k (v zeleném), která bude kolmá na K a prochází body P a Q? Ze dvou bodů kružnici nesestrojíme (musíme tu podmínku kolmosti přetavit v třetí bod).

Protože hledaná kolmá kružnice musí být invariantní vůči inverzi, musí s bodem Q také nutně obsahovat jeho inverzní protějšek Q' (stejně bychom to mohli udělat i s bodem P). No a se třemi body (P, Q a Q') v kapse už hledanou zelenou kružnici (hyperbolickou přímku) hravě sestrojíme: stačí najít osu úsečky QQ', osu úsečky PQ a jejich průsečík bude středem hledané kružnice k.

+++++++++

A ještě jednu souvislost s hyperbolickou geometrií vám ukážu.

Poincarého kruhový model jsme kdysi získali projekcí hyperboloidu do komplexní roviny. Poincarého model poloroviny jsem si ale takříkajíc vytáhl z klobouku. Nebylo vůbec jasné, jak s tím kruhovým modelem souvisí. Teď už vám to mohu prozradit: ten model poloroviny je prostě obrazem kruhového modelu při vhodně zvolené inverzi.

Pojďme tedy najít řídící kružnici K, která zobrazí vnitřek jednotkového kruhu na horní polorovinu (a taky hranici na hranici: tj. červenou jednotkovou kružnici na modrou osu x).

Protože inverze zobrazuje na přímky pouze kružnice procházející středem řídící kružnice, tento střed musí ležet někde na hranici jednotkového kruhu (jinak z něho přímku neuděláme).

Současně ale platí, že body na řídící kružnici se zobrazují samy na sebe. Proto by měla řídící kružnice procházet body P a Q (viz obrázek vpravo), které ponecháme na místě. Střed řídící kružnice tedy musí ležet buď na horním či na spodním "okraji" červené jednotkové kružnice (tj. buď v bodě T=(0,1) anebo S=(0,-1)). Protože ale chceme, aby se vnitřek červeného Poincarého modelu M zobrazil na horní polorovinu (a ne na dolní), nezbyde nám, než si vybrat bod S. Rozmyslete si, že tato (černá) kružnice K skutečně převádí jednotkový kruh na horní polorovinu (a díky vlastnostem inverze zachovává úhly i kružnice). Tedy zachová charakter geometrie. Jen ty zpropadené metriky se musí při přechodu z jednoho modelu do druhého příslušně upravit.

Jako nášup si v této sekci můžete dát Ptolemaiovu větu, která tvrdí, že v čtyřúhelníku ABCD vepsaného do nějaké kružnice je součin délek úhlopříček AB a CD roven

|AC| * |BD| = |AB| * |CD| + |AD| * |BC|

Elegantní důkaz pomocí inverze najdete zde.

+++++++++

Apolloniovy kružnice

Apollonius z Pergy byl starořecký geometr a astronom, který se proslavil zejména svým bádáním na poli kuželoseček. Byl to prostě takový kuželosekáč. A specielně mu učarovaly kružnice.

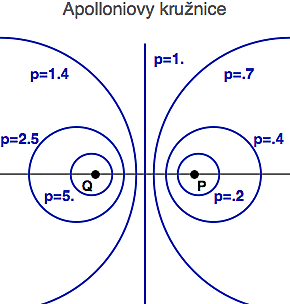
Jedním z problémů, kterými se - v přestávkách mezi sekáním kuželů - zabýval, byl tento: jaké je geometrické místo bodů B, které mají konstantní poměr vzdáleností ke dvěma daným bodům P a Q?

Pozor, neplést s podobnou úlohou, ve které hledáme body s konstantním součtem vzdáleností k daným bodům (ta nás dovede k definici elipsy), popřípadě s konstantním rozdílem vzdáleností (která naopak vede k definici hyperboly). A abychom tuto mezihru měli komplet, tak hledání bodů s konstantním součinem vzdáleností vede k tzv. Cassiniho oválům.

Ke svému překvapení Apollonius zjistil, že řešením zmíněné úlohy jsou kružnice, což se dá ukázat mnoha různými způsoby. Na jeho počest jim říkáme Apolloniovy kružnice. Pro každý poměr dostaneme jednu. Na dalším obrázku je několik takových kružnic vykresleno (modře), včetně konkretní hodnoty poměru p. Jedna z nich (ta uprostřed) je samozřejmě přímka (osa úsečky PQ), jejíž body B mají poměr vzdáleností p = |BP|/|BQ| = 1.

Pomocí dvou zadaných bodů P a Q je ale možné sestrojit ještě jednu zajímavou soustavu kružnic: těch, které těmi body P a Q přímo prochází. Tato soustava je o něco jednodušší, protože se dá celkem lehce zkonstruovat: na ose úsečky PQ si zvolíme libovolný střed O a z něho pak vedeme kružnici s poloměrem OP (která pak nutně protne i bod Q).

Těmto dvěma soustavám kružnic se říká "protínající se" (červená) a "neprotínající se" (modrá) koaxiální soustava (v obou případech se totiž dá ukázat, že mají stejnou tzv. radikální osu). To, co je na nich zajímavé je, že všechny kružnice jedné soustavy protínají všechny kružnice druhé soustavy ortogonálně. Tj. všechny modré Apolloniovy kružnice jsou kolmé na všechny červené kružnice procházející body P a Q (další obrázek vlevo). To se dá ukázat buď algebraicky (např. pomocí komplexních čísel) a nebo geometricky (např. inverzí). Ale trochu se u toho zapotíme.

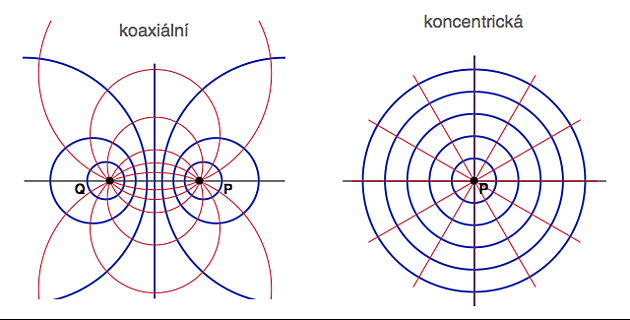
Na dalším obrázku vidíme dvě důležité soustavy kružnic.

Zkusme si levou část obrázku invertovat prostřednictvím řídící kružnice K se středem v bodě Q (a pro určitost třeba s poloměrem r = QP). Tu kružnici K jsem do obrázku nenakreslil, aby nebyl přeplácaný.

Bod P, který na té kružnici K leží se pochopitelně zobrazí sám na sebe (pravá část obrázku). Bod Q se zobrazí do nekonečna a to znamená, že ze všech červených kružnic, které jím procházejí nadělá přímky. A to konkretně přímky procházející bodem P=P' (červené kružnice vlevo prochází bodem P, takže jejich obrazy vpravo musí procházet bodem P'). Otázka je, kam se zobrazí všechny modré kružnice z obrázku vlevo. Na kružnice - já vím. Ale na jaké? Odhadem by člověk řekl, že na koncentrické (obrázek vpravo).

Ukázat to bude ale tak trochu sekce Jauvajs (dnes výjimečně vložená do textu)

Za body P a Q si pro jednoduchost zvolíme body -1 a 1 na ose x. Vezměme si jednu z těch Apolloniových modrých kružnic, označme si její průsečíky s osou x A a B a spočítejme si poměr p = AP/AQ = BP/BQ. S trochou výpočetní námahy získáme x-ové souřadnice bodů A a B: a = (1-p)/(1+p) a b = (1+p)/(1-p). To jsou mimochodem dvě reciproké hodnoty, což už samo o sobě indikuje, že všechny modré kružnice budou nejspíš kolmé na jednotkovou kružnici (což je jedna z těch červených). Ale to jen tak pro zasmání. Pokračujme v jízdě.

Naše řídící kružnice má poloměr r=QP=2 (a střed P v bodě x=-1), takže si lehce spočítáme z rovnice (+), že obrazy A' a B' budou ležet ve vzdálenosti 2+2p a 2-2p od středu Q. Abychom z těchto čísel dostali x-ové součadnice bodů A' a B', musíme od nich odečíst 1, takže dostaneme 1+2p a 1-2p.

To ale znamená, že ať byl poměr p jakýkoliv, obraz příslušné modré kružnice bude procházet body A' a B', které jsou symetricky rozloženy po obou stranách bodu P (x=1). Jinými slovy, všechny modré kružnice se zobrazí na koncentrické kružnice se středem v bodě P (tady si to na další aplikaci můžete vyzkoušet - kromě Apolloniova kruhu určeného dvojicí bodů A a B a poměrem r na ní také najdete jeho inverzi - kružnici kolem bodu B').

Takže si to shrňme.

Červené kružnice vlevo se zobrazují na červené přímky vpravo (procházející bodem P). Modré Apolloniovy kružnice vlevo se zobrazují na modré koncentrické kružnice kolem bodu P. Tyto jsou ale evidentně kolmé na všechny červené kružnice (přímka procházející středem je vždy kolmá na příslušnou kružnici). A protože kruhová inverze zachovává úhly, musí být i všechny červené kružnice vlevo kolmé na všechny modré.

QED

Takže vidíme, že Apolloniovy kružnice jsou de facto inverzním obrazem koncentrických kružnic - a to je jeden z možných způsobů, jak se s nimi nějak vnitřně popasovat.

Není bez zajímavosti, že oba systémy kružnic vedou ke dvěma samostatným souřadným systémům. Z koncentrických kružnic je odvozen systém polárních souřadnic (kde červené a modré kružnice ukazují množiny, na kterých je každá z obou souřadnic konstantní), zatímco z Apolloniových kružnic se dají odvodit bipolární souřadnice. Ty jsou ovšem o něco exotičtější a musím se přiznat, že v praxi jsem se s nimi zatím nesetkal.

+++++++++

A jak to souvisí s hyperbolickou geometrií?

Důležitou charakteristikou každé geometrie jsou koncentrické kruhy (kolem nějakého středu P). Ty de facto vymezují, kam jsme schopni se z daného bodu P za určitý časový úsek dostat.

Zkusme se zamyslet, jaké jsou koncentrické kružnice v Poincarého modelu poloroviny.

Zvolme si někde bod P a k němu pak symetrický bod Q (na druhé straně osy x - kde ho plošníci nevidí neb je "za horizontem). Osa x tak bude součástí koaxiálního systému Apolloniových kružnic určených body P a Q (je to ta přímka na níž je poměr p roven 1).

Vtip je v tom, že když si k ní domalujeme ty ostatní kružnice, tak to, co se nám jeví jako soustava koaxiálních kružnic se plošníkům bude jevit jako koncentrická soustava.

Toto se dá nahlédnout buď algebraicky a nebo geometricky.

Aby se nám to algebraicky lépe počítalo, zvolíme si bod P = (0,1). Bod Q pak má souřadnice (0,-1). Každá z těch modrých koaxiálních kružnic je kolmá na kružnici K (to je jedna z těch protínajících body P a Q), takže body S a J jsou navzájem inverzní a mají proto reciproké souřadnice y. Řekněme S = (0,y) a J=(0,1/y).

Minule jsme viděli, že pro hyperbolické vzdálenosti podél vertikál stačí spočítat logaritmus poměru y-ových souřadnic.

A protože poměr y:1 (pro cestu z bodu S do bodu P) je stejný jako poměr 1:1/y (pro cestu z P do J), vidíme, že z pohledu plošníků je bod P skutečně na půli cesty z S do J. Obdobně se to dá spočítat i pro ostatní "přímky" (tj. geodetiky) procházející bodem P - jen musíte použít pro vdálenosti komplikovanější formulku.

Geometricky se to dá nahlédnout přímo.

Přímky (geodetiky) procházející bodem P jsou "baj definišn" kružnice kolmé na osu x a to znamená, že musí automaticky procházet také bodem Q (ten co je "schovaný" pod osou x). Jsou to tedy ty červené kružnice. Z pohledu plošníků musí být jejich "koncentrické kružnice" na ty červené "přímky" kolmé. Budou to tedy ty (z našeho pohledu) modré Apolloniovy kružnice.

Jejich nalezení není v modelu poloroviny žádný problém, protože s každým bodem P se ten bod Q nalezne lehce ze symetrie (bod Q je de facto zrcadlovým obrazem P') a jakmile máte dva body, můžete začít vesele konstruovat Apolloniovy kružnice (tj. z pohledu plošníků koncentrické kruhy).

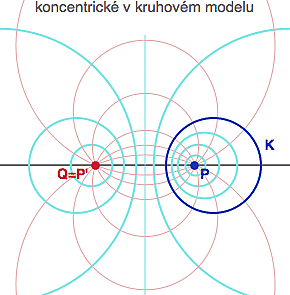
Pro kruhový model je to trochu komplikovanější, protože máte zadanou pouze jednotkovou kružnici K a vnitřní bod P a chtěli byste opět vědět, jak vypadají koncentrické kruhy (z pohledu plošníků) kolem tohoto bodu.

Tady není na první pohled jasné, kde by ten bod Q měl vlastně být, abychom si z něho mohli Apolloniovy kružnice nabrnkat. Ale vzpomeneme si, že kružnice procházející dvojicí inverzních bodů jsou kolmé na řídící kružnici, takže si nejprve spočítáme inverzi bodu P vzhledem k modré jednotkové kružnici K (ta byla pro tyto účely povýšena do hodnosti řídící kružnice) a z něho nakonec dostaneme bod Q=P', který nám umožní vybudovat zbytek koaxiálního systému.

I zde se dá ověřit, že ze středu P je to k obvodu každé bledě modré kružnice skutečně stejně daleko (v hyperbolickém smyslu), ale výpočet je podstatně zapařenější (kruhový model má komplikovanější metriku).

Komu to takhle nestačilo, může si dát nášup v podobě křížového poměru, což je velice zajímavá veličina (v podstatě poměr poměrů), která k tomu výpočtu vzdáleností v kruhovém modelu slouží.

+++++++++

Möbiovy transformace

S rozvojem komplexní analýzy v 19. století se celá řada klasických geometrických technik v rovině začala výpočetně realizovat pomocí komplexních čísel (namísto klasických souřadnic x-y).

Jedním z nejrozšířenějších nástrojů této analýzy se staly Möbiovy transformace, které v sobě přirozeně zahrnují většinu klasických geometrických transformací (včetně inverze).

Z algebraického pohledu se jedná o lineární lomené funkce v komplexní proměnné z.

(++) M(z) = (az+b) / (cz + d), kde a,b,c a d jsou komplexní čísla

(je to tedy v podstatě podíl dvou lineárních polynomů)

Již dříve jsme si ukázali, že taková zobrazení se dají nahlédnout jako projektivizace určitých matic. A skládání takových transformací pak odpovídá maticovému násobení. Dnes nás ale bude zajímat jejich geometrický aspekt. 

Pro konkretně zadané hodnoty koeficientů a,b,c,d samozřejmě není problém spočítat obraz jakéhokoliv komplexního čísla z (je to jen několikanásobná aplikace běžných algebraických operací). Jenže to, že si spočítáme pár hodnot této transformace nám neposkytně dostatečně plastický obraz toho, jak vlastně funguje (tedy co s celou komplexní rovinou provádí).

Proto si ji pojďme rozložit na několik elementárních případů, jejichž globální akce bude pro naši geometrickou intuici stravitelnější.

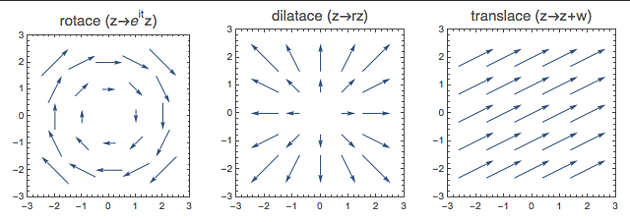
1. M(z) = z + a

je prostě translace (pravá část obrázku)

Komplexní násobení M(z) = az se dá geometricky uchopit pokud si koeficient a napíšeme v polárním (goniometrickém) tvaru a = r cos(t) + i r sin(t) = r exp(it). Pak můžeme zapřáhnout další dvě známé geometrické transformace a zašifrovat je do speciálních případů Möbiových transformací:

2. M(z) = r z

bude (pro reálné číslo r) dilatace - tedy "nafouknutí" roviny z počátku

3. M(z) = exp(it) z

je komplexní zápis rotace kolem počátku (t je úhel rotace).

Pro pozdější diskusi připomenu, že jak dilatace, tak rotace fixuje bod 0 a v jistém smyslu také nekonečno (komplexní nekonečno se rotací ani dilatací nikterak nepřiblíží - tj. zůstane stále nekonečnem).

+++++++++

Zatím je to všechno krásné, ale skládáním těchto tří transformací (translace, rotace a dilatace) se budeme stále plácat jen v říši lineárních polynomů. Abychom mohli Möbiovy transformace skutečně prokouknout, musíme zjistit, co se s komplexní rovinou děje pokud aplikujeme reciprokou hodnotu komplexního čísla (jen ta nám umožní šachovat i se jmenovatelem):

M(z) = 1/z

Číslo z si opět zapíšeme v polárním tvaru z= r exp(it) a dostaneme 1/z = (1/r) exp(-it). Polární souřadnice r se tedy změnila na svou reciprokou hodnotu (inverze vzhledem k násobení), zatímco souřadnice t (úhel) se změnila na svou opačnou hodnotu (inverze vzhledem ke sčítání). Aby toho nebylo moc najednou, podívejme se nejprve na komplexní číslo 1/zŻ = (1/r) exp(it). Toto číslo je kruhovou inverzí čísla z vzhledem k jednotkové kružnici K se středem v 0: leží na stejném paprsku a součin jejich vzdáleností od středu je čtverec poloměru: r(1/r)=12, což je rovnice (+) z úvodu. Hledané číslo 1/z je pak evidentně číslem komplexně sdruženým k 1/zŻ (de facto zrcadlení v ose x).

To znamená, že reciproká hodnota 1/z není z geometrického pohledu nic jiného než kruhová inverze složená se zrcadlením. A máme poslední ingredienci potřebnou k úplnému pochopení Möbiových transformací. Kromě běžných (a ze školy dobře známých) transformací obsahují také kruhovou inverzi. A ta jim propůjčuje jejich kouzelné vlastnosti.

Jakmile víme jak se chová funkce M(z)=1/z, můžeme ji začít skládat s výše uvedenými lineárními funkcemi na komplikovanější výrazy, např. M(z) = 1/(az+b). Vhodnou algebraickou manipulací všech 4 elementárních transformací si tedy nabrnkáme libovolnou Möbiovu transformaci (podrobněji třeba zde). Jejich vizualizaci si můžete procvičit v tomto videu.

Z vlastností těch elementárních komponent dostaneme, že Möbiovy transformace zachovávají kružnice i úhly (jsou tedy konformní). Tady byste sice mohli namítnout, že kruhová inverze obrací orientaci úhlů, jenže to následné zrcadlení ji zase hezky vrátí nazpátek.

+++++++++

Jinou možností rozkladu Möbiových transformací (a jejich následné klasifikace) je pak převedení jejich algebraické formy (++) do tzv. normálního tvaru (který nám umožní na ně pohlížet jako na speciální příklady lineární transformace M(z) = mz). Je to proces, který trochu připomíná diagonalizaci matice A, kdy hledáme nějakou přechodovou matici P, která ji převede na diagonální tvar: PAP?1=D.

V prvním kroku musíme najít pevné body Möbiovy transformace (++), tedy komplexní čísla, která se zobrazují sama na sebe

M(z) = (az+b)/(cz+d) = z

Výše uvedená kvadratická rovnice (vynásobte si obě strany jmenovatelem) bude mít v komplexní rovině dvě řešení, která si označíme r a s. Myšlenka je celkem jednoduchá: jedno z těch čísel pošleme do 0, druhé do nekonečna a zjistíme, že ty pevné body hrají v jistém smyslu roli pivotních bodů P a Q z předchozí sekce.  Za tímto účelem si zavedeme pomocnou přechodovou transformaci (de facto změnu souřadnic) F rovnicí

F(z) = (z-r)/(z-s)

I toto je Möbiova transformace (protože pevné body r a s jsou komplexní čísla), která evidentně převádí r na 0 a s na nekonečno (a inverzní transformace naopak):

F(r) = 0 a F(s) = ?   a pro inverzi platí: F?1(0) = r  a F?1(?) = s

Uvažujme teď složení těchto tří Möbiových transformací

M'(z) = F(M(F?1(z)))

Tato transformace fixuje 0 a ?.

Proč?

Když tu pravou stranu rozpleteme, zjistíme, že z=0 se nejprve zobrazí na r pomocí F?1, následné M nechá r beze změny (r je pevný bod M) a to "vnější" F pak vrátí bod r do 0. Takže M'(0) = 0 a obdobně se ukáže, že M'(?) = ?.

Rozmyslete si, že zobrazení, které fixuje 0 a ?, musí mít tvar

M'(z) = m z, kde komplexní číslo m je tzv. multiplikátor

(nápověda: Möbiova transformace (az+b)/(cz+d) která fixuje 0, musí splňovat b/d=0 a tedy b=0. Obdobně transformace, která fixuje nekonečno musí splňovat c=0 - jinak by limita pro z blížící se nekonečnu byla konečná)

Chování M' ale známe. Rozložíme si m opět na polární činitele a dostaneme složení rotace a dilatace. Specielně, pokud je m reálné, dostaneme čistou dilataci, pokud je m komplexní jednotka (m = exp(it)), bude M' čistá rotace. Teď ale navíc víme, mezi kterými body (r a s) tyto transformace fungují.

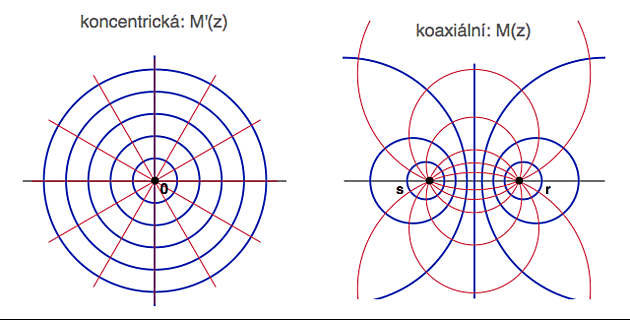
Připomeňme si předchozí obrázek koncentrických a koaxiálních kružnic (ve kterých se akce M a M' dají přirozeně studovat).

Nejprve levá část, kde řádí jednodušší M'. Rotace nechává ty modré kružnice invariantní a ty červené kružnice (zde přímky) otáčí jednu na druhou. Dilatace naopak ponechává ty červené přímky invariantní, zatímco modré kružnice "nafukuje" jednu na druhou. Hezky bod po bodu.

A protože přechodové zobrazení F je též Möbiova transformace (tj. v podstatě inverze plus nějaké to posunutí či pootočení), převádí červené přímky vlevo (což jsou přesně "kružnice" procházející 0 a ?) na červené kružnice vpravo (procházející body r a s). Tím pádem modré kružnice vlevo (které jsou kolmé na červené přímky) musí nutně převést na kružnice kolmé k těm červeným a to jsou jsou naše staré dobré známé Apolloniovy kružnice (pouze s body r a s v rolích P a Q).

Jinými slovy, to co zobrazení M' provádí v levé části obrázku, M provádí v pravé.

To, co to konkretně je, se pozná podle multiplikátoru m.

Möbiovy transformace s reálným multiplikátorem se chovají podobně jako dilatace (posunují nás podél červených kružnic vpravo -  pěkně z jednoho pevného bodu do druhého - stejně jako nás klasická dilatace posunuje z 0 do nekonečna), zatímco komplexní jednotkový multiplikátor implikuje zobrazení, která se podobají naším rotacím (posunují nás podél modrých kružnic vpravo). Těm prvním říkáme hyperbolické transformace a těm druhým eliptické. A protože hodnoty těch multiplikátorů m se obvykle dostanou řešením výše uvedené rovnice pro pevné body, dají se odvodit explicitní podmínky pro typy transformací přímo z definičních koeficientů (podrobnější výklad a klasifikace je na anglické wiki).

Pokud vás zaráží, že v tom normálním tvaru je Möbiova transformace určena třemi komplexními čísly (m,r,s), zatímco v tom algebraickém čtyřmi (a,b,c,d), považte, že ten algebraický tvar je podíl a proto v něm můžeme bez obav jeden z těch (nenulových) koeficientů zkrátit - tím na jeho místě dostaneme jedničku a zbylé tři koeficienty jsou pak parametry té transformace.

Proto má také většina praktických úloh tvar: najděte Möbiovu transformaci, která převádí tyto tři body (komplexní čísla) na nějaké jiné. K určení těch tří parametrů totiž potřebujeme tři rovnice (příklad zde).

Podobně postupujeme, pokud chceme najít Möbiovu transformaci, která převádí Poincarého kruhový model na model poloroviny (to je často výpočetně výhodnější než hledat příslušnou inverzi geometricky). Stačí si zvolit tři body na jednotkové kružnici, tři body na ose x (hranice poloroviny) a hledat pak Möbiovu transformaci, která příslušná komplexní čísla na sebe převádí (to nám dá obecnější řešení než ta výše uvedená inverze).

Nejjednodušším příkladem takového zobrazení je

M(z) = i(1+z)/(1-z)

které evidentně převádí tři body jednotkové kružnice (konkretně z=-1,1,i) na tři body na ose x (z=0,?,-1). Podrobnosti zde.

+++++++++

A jakou to má souvislost s hyperbolickou geometrií?

Möbiova transformace s reálnými koeficienty, zobrazuje reálnou osu na sebe a z pohledu plošníků, žijících v modelu poloroviny, se pak pravá část předchozího obrázku dá interpretovat takto. Pokud jsou body r a s komplexně sdružené, tak ty hyperbolické transformace (posunující podél červených kružnic) se plošníkům budou jevit jako dilatace (červené kružnice jsou z jejich pohledu přímky procházející bodem r), zatímco ty eliptické se jim budou jevit jako rotace (modré kružnice jsou z jejich pohledu koncentrické vzhledem k bodu r). Plošníci ten druhý bod s samozřejmě nevidí, což ale jejich iluzi dilatace a rotace jen podporuje.

(Ale pozor, jako rotace se toto zobrazení jeví plošníkům proto, že ty červené kružnice převádí jednu na druhou podél těch modrých. Z našeho pohledu to ale rotace nejsou - to je vidět například z toho, že jedna z těch červených kružnic vpravo je ve skutečnosti přímka - osa x. Eukleidovská rotace nikdy z kružnice přímku neudělá).

Jakousi obdobou translace je pro plošníky Möbiova transformace jejíž pevné body leží na hraniční přímce (jsou to tedy - jak naznačeno na předchozím obrázku - reálná čísla r a s). Pokud bude příslušný multiplikátor m reálný, bude zobrazení posouvat body podél červených kružnic spojujících body r a s. Ty už ale nejsou komplexně sdružené (jsou reálné), takže pouze jedna z těch červených kružnic, říkejme jí p, bude hyperbolická přímka (tj. kružnice kolmá na hraniční kružnici). Ty ostatní už přímkami nejsou - mají ale zajímavou vlastnost, že jsou od té hyperbolické přímky p konstantně vzdálené (v hyperbolickém smyslu). To kontrastuje s Eukleidovským případem, kde posunujeme vesměs podél přímek.

Hyperbolická rovina (ať už ten či onen model) je ovšem velmi bohatý útvar a má některá geometrická zobrazení, kterými eukleidovská rovina neoplývá vůbec.

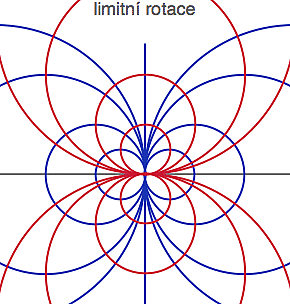
Pokud například ty dva pevné body r a s splynou (a to se může lehce stát - kvadratické rovnice mohou mít dvojici identických kořenů), pak ty modré a červené koaxiální systémy kružnic zdegenerují jak je naznačeno na obrázku vpravo, byť jsou na sebe oba systémy stále kolmé. Příslušná transformace (tzv. limitní rotace) pak opět posunuje body podél těch či oněch kružnic.

Něco takového už v běžné rovině nenajdete. Kružnice, které se dotýkají té hraniční se mimochodem jmenují horocykly a mají spoustu zajímavých vlastností (např. nekonečnou délku anebo to, že všechny kolmé přímky vedou z horocyklu do ideálního bodu, kde se dotýká hraniční kružnice). Ale to už by nás zavedlo příliš hluboko do hyperbolického pralesa.

Kdo by se jím chtěl prosekat, může si místo mačety sehnat výbornou knížku Tristana Needhama Visual Complex Analysis, která se tématem dnešního Matykání zaobírá detailně a hlavně fundovaně.

+++++++++

A abych Vás v půjčovně čtenářů nevracel v takto zničeném stavu, vylovím vám z westernového muzikálu Paint Your Wagon píseň "I'm on My Way". Složila ji stejná autorská dvojice jako známý muzikál My Fair Lady: tedy skladatel Frederick Loewe a textař Alan Jay Lerner. Mimochodem, to doprovodné video není ukázka z filmu, ale montáž dobových zlatokopeckých dokumentů plus ukázky pracovního procesu. A pokud náhodou neznáte význam slova 'zlatokop' - tak to je někdo, kdo kope do mičudy tak obratně, že si vyslouží zlatou medaili a postup do 1. ligy - včera např. fotbalisté FC Hradec Králové. Ale teď už vážně. Frederick Loewe: I'm on My Way (rozuměj: "on my way to the first league")

Předchozí díly Matykání.