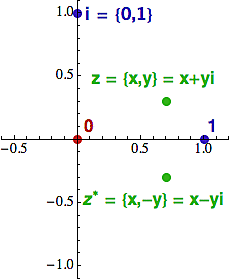Matykání: komplexní čísla
Komplexní čísla mají u široké veřenosti pověst excentrického strýce, kterému je lepší se při rodinné slezině vyhnout velkým obloukem. V této minisérii se pokusím vás přesvědčit, že tito číselní exoti nejsou zase až tak bizarní, v mnoha ohledech jsou funkčnější než reálná čísla a jejich analýza patří k esteticky nejkrásnějším partiím matematiky (mimochodem, první fraktály vzešly právě z iterací komplexní kvadratické funkce).
Pokud se díváte na kvantitativní svět prizmatem reálných čísel, je to jako byste se dívali na taneční číslo přes osvětlenou zástěnu a viděli de facto pouze stínové obrysy všech figur. Na tom samozřejmě není nic špatného. I z dobré siluety se toho o povaze tance a umění tanečníků můžete hodně dozvědět. Pokud si ale chcete užít představení ve vší jeho mnohotvárnosti, plasticitě a barvitosti, bude lépe, když zástěnu sundáte a podíváte se na tu taneční kreaci přímo. A takový pohled vám skýtají komplexní čísla.
Během své matematické kariéry jsem si všiml, že matematici se v zásadě dělí na dvě kategorie, podle toho jak přistupují k důkazům tvrzení, kterými se pokouší zmapovat kvantitativní svět.
Jedni si k danému problému dokáží nakreslit správný obrázek a z něho ty vztahy mezi veličinami prostě "vykoukají". Těm říkám "pozorovatelé". Ti druzí si do notýsku napíšou nějakou změť symbolů a rovnic a pak s ní cloumají tak dlouho, až z ní vyleze, co potřebují. Takovým říkám "manipulátoři". Přirozenou doménou "pozorovatelů" je geometrie, zatímco "manipulátory" najdete spíše ve vodách algebraických. A protože nevím, do které skupiny patříte, podíváme se na komplexní čísla z pohledu algebraického i geometrického.
(jako obvykle 2*3 a občas také 2.3 bude dva krát tři a 2^3 bude dvě na třetí)
+++++++++
Komplexní čísla - pohled algebraický
(prebambule)
Číselné systémy vznikly jako odpověď na odvěkou lidskou potřebu zkrotit kvantitu. Jejich vývoj byl v mnoha směrech spoluurčen naší schopností, respektive neschopností, řešit některé typy rovnic. Na počátku dlouhé cesty stála celá čísla, která odpovídala těm nejjednodušším kvantitám - jeden král, dva písaři, tři sestry, čtyři z tanku a pes. A v celých číslech se dala vyřešit celá spousta užitečných rovnic - například úloha "kolik máme jablek, pokud ztrojnásobením jejich počtu dostaneme 18?" se dá přepsat do úhledné rovnice 3x = 18 a snadno vyřešit: x=6.
Malý problém vznikne, pokud se pokusíme řešit rovnici 3x = 17. Žádné celé číslo nesplňuje podmínky naší rovnice a proto žádné celočíselné řešení neexistuje, přestože koeficienty jsou celá čísla. Všimněte si, že naše neschopnost najít řešení není chybou té rovnice. Na té není nic závadného. Problém je v tom, že jsme si vybrali příliš omezený číselný systém. Pokud celá čísla trochu rozšíříme a začneme počítat i se zlomky (tedy s racionálními čísly), řešení se objeví v cukuletu: x= 17/3.
Podrobnější analýzou se ukázalo, že každá lineární rovnice s racionálními koeficienty má v racionálních číslech skutečně řešení. A nad královstvím matematiky se rozklenula široká duha harmonie a pohody. Až do okamžiku, kdy nějaký koumák pocítl nutkavou potřebu udělat si doktorát a vynalezl kvadratickou rovnici.
I relativně jednoduchou kvadratickou rovnici x2 = 2 se zlomky nevyřešíte ani kdybyste se rozkrájeli na malé kousky a pokapali citronem. A tak matematikům nezbylo než vyhrnout si pouzdra logaritmických pravítek a číselný systém opět o pár jízdních pruhů rozšířit. Tentokrát k racionálním číslům přidali čísla iracionální a dostali tak systém reálných čísel, ve kterém se řešení opravdu nalezlo. Jmenuje se odmocnina ze dvou, alias sqrt(2). Alelůja!
Jásot to byl ovšem předčasný. Ve staré věži sídlila jedna zapomenutá kvadratická rovnice x2 = -1 a ta se řešení v reálných číslech úspěšně vzepřela. Žádné reálné číslo na druhou nemůže být záporné a basta fidli. A tak matematikům nezbylo než rozšířit číselný systém ještě jednou a doufat, že se vzpurná rovnice poddá.
(bambule)
Jak rozšířit reálná čísla není na první pohled patrné. Číselná osa se rozkládá od mínus nekonečna do plus nekonečna a desetinná čísla ji vyplňují tak hustě, že na ní nezaparkujete motorku, natož pak nové číslo. Ale matematici nejsou žádná béčka. Když se něco nevyskytuje přirozeně ve volné přírodě, tak si to vysoustruží ve svých vyšinutých myslích.
Jedné tmavé noci se rada starších počtářů sešla v rozeklané rokli na okraji městečka a za rituálního hučení si z večerního oparu utkala pozoruhodné číslo i, které má tu vlastnost, že když ho umocníte na druhou, dostanete -1. To je jeho základní charakteristikou a nic jiného o něm zatím předpokládat nebudeme. Nevíme, zda je větší než 3 nebo menší, nevíme zda je sudé nebo liché a netušíme jaký je jeho desetinný rozvoj - pokud tedy vůbec nějaký má. A protože na reálnou osu se toto číslo upíchnout nedalo, jediná kopie tajemného íčka, odlitá ze slitiny platiny a iridia, byla uložena do sklepa u pana Marečka v Náchodě (všechny regály v Sevres u Paříže už byly naplněné až ke stropu).
Prvním úkolem íčkových spiklenců bylo zjistit, zda se nové číslo chová rozumně. Pokud chcete v matematice něco rozšířit, musíte v první řadě zaručit, že to nezbortí stávající konstrukci a bude to respektovat vžité konvence a zákonitosti (to je jako když vypustíte novou verzi softvéru - ta musí být také zpětně kompatibilní - jinak vám ji uživatelé omlátí o hlavu).
Nejprve se podíváme, co se stane, když nové číslo i vynásobíme nějakým reálným číslem, třeba 5. Protože (a*b)2 = a2 * b2, musí platit: (5i)2 = 52 * i2 = 25 * (-1) = -25. Číslo 5i je tedy odmocninou z -25 a jako takové splňuje kvadratickou rovnici x2 = -25. Podobné je to i s ostatními násobky íčka, kterým souhrnně říkáme imaginární čísla. Jejich čtverce pokryjí celou číselnou osu nalevo od nuly. Odmocnit libovolné záporné číslo je teď hračka, srovnatelná s výměnou žárovky. Např. sqrt(-8) = sqrt(-1)*sqrt(8) = 2,82843 i. Pomocí imaginárních čísel se dostaneme na kobylku mnoha kvadratickým rovnicím.
Zatím jsme ovšem náš číselný systém nijak nerozšířili. Pouze jsme si vytvořili jakousi paralelní verzi reálných čísel, která nám umožňuje odmocnit to, co se doposud odmocnit nedalo. V reálném hájemství jsou čtverce všech čísel kladné, zatímco v tom imaginárním jsou záporné. Matematika ale nemůže mít dva nezávislé světy, které spolu - jako Shakespearovi Montekové a Kapuleti - vůbec nekomunikují. To by z ní pak vznikla banánová republika, rozdělená do několika ghett s nerovnými podmínkami.
Abychom z reálných a imaginárních čísel uvařili nějakou smysluplnou soustavu, obrátíme se k odbornici na slovo vzaté: Magdaleně Dobromile Rettigové.
Představte si, že máte k disposici dvě misky. Do jedné vyklopíte pár vajec a do druhé vysypete pytlík mouky. A teď si vezmete řekněme dva váhové dílky vajec, přidáte tři dílky mouky a hned máte těsto ke kuchtění. Symbolicky bychom ho mohli zapsat jako T = 3M + 2V, kde M a V jsou nějaké váhové jednotky vajec a mouky - třeba 100 gramů. Pokud bychom chtěli něco trochu hustšího, vezmeme si jeden díl vajec, přidáme 5 dílů mouky a máme vystaráno: T = 5M + 1V. Hustota ucházející. A ta množství mohou být samozřejmě jakákoliv (kladná) reálná čísla. Vezmete-li 3.3 dílů vajec a 2.9 dílků mouky dostanete těsto zrovna tak: T = 2.9M + 3.3V.
Komplexní čísla jsou de facto takovým matematickým těstem. Vezmete si třeba 3 dílky reálných čísel, přidáte dva dílky imaginárních a dostanete něco, čemu říkáme komplexní číslo (a obvykle ho značíme písmenkem z):
z = 3r + 2i
kde r je jednotka reálných čísel (prachobyčejná reálná jednička r=1) a i je ono tajuplné číslo zamknuté ve sklepě pana Marečka (jednotka čísel imaginárních). A protože nemá cenu psát 3r tam kde můžeme jednoduše napsat 3*1 = 3, zapisujeme výsledné číslo ve tvaru:
z = 3 + 2i
(2i samozřejmě znamená 2*i)
Na rozdíl od těsta paní Rettigové, kde můžete používat jen kladné kombinace vajec a mouky, si můžete u komplexních čísel tu reálnou a imaginární složku nakombinovat v jakémkoliv poměru:
z=3,3 - 2,7i
(a pokud tu reálnou jednotku chcete vidět explicitně, tak: z=3,3r - 2,7i)
Samozřejmě jak reálná, tak imaginární čísla jsou v tomto systému obsažena. Reálná 5 není nic jiného než 5+0i a imaginární číslo 6i se dá napsat jako 0+6i. Takže jak Montekové, tak Kapuleti teď žijí v jednom komplexním domečku a musí chtě nechtě tahat za jeden provaz.
Úplně hotovi ale ještě nejsme. Abychom ukázali, že naše "těsto" je skutečně číselným systémem, musíme v něm jednak zavést aritmetické operace a jednak ukázat, že při provádění těchto operací z našeho systému nevypadneme - tedy že výsledkem každé takové operace bude opět číslo z našeho systému. Například z imaginárních čísel jako takových při provádění násobení vypadneme. Součin dvou imaginárních čísel není číslo imaginární, ale reálné: (2i)*(3i) = -6. Proto musíme ukázat, že pro komplexní čísla k tomuto politováníhodnému nedopatření nedojde. A to ani jednou za deset let. Představte si tu hrůzu ve tváři Magdaleny Dobromily, kdyby vzala dva druhy moukovaječného těsta, chvilku je v díži hnětla a po chvíli zjistila, že má v díži rizoto - tedy objekt z úplně jiného nutričního systému.
+++
Sčítání komplexních čísel je jednoduché a probíhá podle pravidla "hrušky s hruškama a jabka s jabkama". Takže íčka na jednu hromadu a všechno bez íček na druhou. Lehce si ověříte, že výsledkem bude opět komplexní číslo.
(2+3i) + (3+4i) + 10 = 15 + 7i
(jak bylo řečeno výše, tu desítku si představujeme jako 10 + 0i)
Násobení je trochu komplikovanější a je založené na násobení mnohočlenů. Abychom do toho nespadli po hlavě, ukážu vám nejdřív příklad pro dvě reálná čísla obsahující konstantu ? (3,14). Často je výhodné ji nazapisovat desetinně, ale počítat s ní symbolicky, abychom dostali lepší náhled do struktury výsledného čísla. Tady je malý příklad takového násobení:
(4+3?) * (1+2?) = 4 + 8? + 3? + 6?2 = 4 + 11? + 6?2
Součin komplexních čísel funguje úplně stejně, jenom s tím rozdílem, že na rozdíl od píčka nenajdete íčko na číselné ose (co by tam taky dělalo, když je zamčené ve sklepě pana Marečka). Na druhé straně ale můžete využít skutečnosti, že jeho čtverec je i2=-1 a to vám umožní zjednodušit výsledek (poslední rovnost níže):
(4+3i) * (1+2i) = 4 + 8i + 3i + 6i2 = 4 + 11i - 6 = -2 + 11i
Všimnete si, že právě díky tomu, že i2=-1 je součin dvou komplexních čísel opět komplexní číslo. Jinak by nám ve výsledku pořád plavalo i2 a v podstatě bychom se ho nemohli zbavit - museli bychom ho zase nějak přifařit k číselnému systému (a posléze i vyšší mocniny i a to už by zavánělo akutní bolestí hlavy).
Takto jsme získali číselný systém, ve kterém můžeme nejen provádět běžné aritmetické operace (odečítání a dělení vám ukážu v závěru), ale navíc v něm můžeme odmocňovat záporná čísla, takže žádná kvadratická rovnice už nebude bez řešení. Např. x2=-9 nás dovede k výsledku x = sqrt(-9) = sqrt(-1)*sqrt(9) = 3i (a druhé řešení je x = -3i).
Jako cvičení si můžete zkusit vyřešit kvadratickou rovnici x2-4x+29 = 0. Standardní středoškolská formulka by vám měla vydat dvě řešení: x = 2+5i a x = 2-5i. V reálných číslech ta rovnice řešení nemá.
(postbambule)
Násobení dvojčlenů je v podstatě dvojitá aplikace distributivního zákona. Nejprve předstíráte, že výraz vpravo je jedno číslo a roznásobíte závorku vlevo a pak ho použijete ještě dvakrát na oba nově vzniklé výrazy. Symbolicky (a zatím bez íček):
(a+b)*(c+d) = a*(c+d) + b*(c+d) = a*c +a*d + b*c + b*d
Američtí studenti mají na tento typ výpočtu takovou celkem šikovnou mnemotechnickou pomůcku, která jim umožní ten mezikrok vynechat a spočítat to rovnou z jedné vody načisto. Říkají tomu "metoda FOIL" (což je zkratka pro First - Outer - Inner - Last). Česky to znamená, že vynásobíte První pak Vnější pak Vnitřní a nakonec Poslední členy v obou úvodních závorkách a máte výsledek hned. Můžete si to zkusit na následujícím komplexním součinu (a nezapomeňte, že i2=-1):
(2 + 5i)*(3 + 8i) = 6 + 16i + 15i - 40 = -34 + 31i
+++++++++
Komplexní čísla - pohled geometrický
(prebambule)
Jedna věc, která mne na našem vesmíru nepřestává fascinovat je jednorozměrnost jeho kvantitativního ústrojí. Ať se podíváte na hmotnost hvězd, vzdálenost mezi Brnem a Prahou či obsah Máchova jezera, každé množství se dá reprezentovat jako reálné číslo na jednorozměrné číselné ose.
Ta jednorozměrnost odpovídá intuitivní představě, že něčeho může být trochu více (a reprezentovaná kvantita se pak posouvá na číselné ose doprava) a nebo trochu méně (příslušné číslo se posouvá doleva), ale neexistuje situace, kdy by se daná kvantita posunovala jaksi "šejdrem".
Hezky tuto představu odráží stará stolní váha, jejíž jazýček se vychyluje vpravo, pokud přidáváte váženou hmotu a vlevo pokud ji ubíráte, ale nikdy se nedostanete do situace, kdy by jazýček trčel kolmo ven z přístroje. Kvantita je zkrátka jako tramvaj - zná pouze jeden směr (dopředu - dozadu) a nikam jinam se ubírat nedokáže.
Z praktického pohledu inženýra je tím věc uzavřená.
Matematik obecný je ovšem tvor z čeledi šťouravých (rod neodbytní) a jedné vlahé červnové noci nějakého obzvlášť agilního jedince napadlo, co by se asi tak stalo, kdyby naše kvantity měly volant a dokázaly jet nejen dopředu a dozadu, ale taky třeba mírně doprava (tedy že by něčeho bylo více a současně trochu "stranou"). A znáte to. Jakmile vám někdo nasadí brouka do hlavy, je konec. A tak si slovutní mistři, páni magistři začali lámat hlavu, zda by se číselná osa nedala nahradit číselnou rovinou (a kolik by taková výměna asi stála).
(bambule)
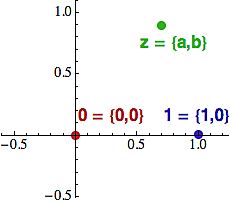
Protože na číselné ose je každé číslo reprezentováno bodem, první krok k vytvoření dvourozměrného číselného systému je celkem jasný. Každý bod roviny bude reprezentovat nějaké "číslo", s tím, že body na ose x budou hrát tradiční roli reálných čísel, tak jak je známe. Na obrázku je vyznačená 0 a 1. Pro souřadnice těchto bodů budu používat kroucené závorky - viz např. zelený bod z = {a,b}, který má v tomto konkretním případě hodnotu {0.7,0.9}.
Jedinou otázkou, kterou musíme dořešit, je jak pro tyto body definovat aritmetické operace, tak aby splňovaly všechny zákony, které od nich očekáváme, a aby se na reálné ose chovaly přesně jako stará dobrá reálná čísla.
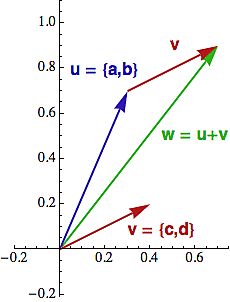
Sčítání je nejjednodušší - definujeme ho po složkách (jako bychom sčítali vektory).
{a,b} + {c,d} = {a+c,b+d}
Na obrázku vpravo je "číslo" w součtem u + v. Lehce si ověříte, že takto definovaná operace je asociativní i komutativní a pokud se omezíte na reálná čísla (tj. druhá souřadnice bude rovna 0), dostanete klasické sčítání
{a,0} + {c,0} = {a+c,0}
Jak jsme viděli nahoře, roli nuly převzal bod {0,0}, takže pokud ho přičteme k libovolnému bodu, nic by se nemělo změnit - což je přesně chování, které od nuly očekáváme.
{a,b} + {0,0} = {a,b}
Povzbuzeni tímto úspěchem, zkusíme definovat násobení bodů taktéž "po složkách"
{a,b} * {c,d} = {a*c,b*d}
To nám ale bohužel neprojde, protože chceme, aby naše stará dobrá reálná jednička (tedy bod {1,0}) měla stále tu vlastnost, že když s ní pronásobíme libovolné číslo, jeho hodnota se nesmí změnit. A to už nefunguje.
{a,b} * {1,0} = {a,0}
Mohli bychom to samozřejmě zařídit jinak a rolí jedničky pověřit bod {1,1}:
{a,b} * {1,1} = {a,b}
Tady už by to fungovalo, jenže kromě toho, že jsme drze posunuli jedničku mimo reálnou osu (takže už to nebude rozšíření starého systému) máme na krku další průšvih. S takto definovaným násobením můžeme vzít dvě nenulová čísla (body) a součinem z nich dostat nulu (a to je pro číselný systém, který budujeme, nepřípustné - v reálných číslech něco takového taky není možné).
{a,0} * {0,b} = {0,0}
Takže tudy cesta nevede. Musíme zpátky k rýsovacímu prknu.
+++
Tímto malým nezdarem chci jenom říci, že cesty matematiky nejsou vždy přímočaré a někdy není jasné jak danou operaci zobecnit. V tomto případě je nutno ty složky trochu namíchat. Nebudu vás dlouho trápit a prozradím vám, že cesta ke kompatibilnímu součinu bodů vede přes následující koktejl:
{a,b} * {c,d} = {a*c-b*d,a*d+b*c}
Ten sice vypadá trochu jako trest za rozbité okno v tělocvičně, ale teď už se reálná jednička - bod {1,0} - bude chovat tak, jak má (tj. něco krát jedna bude to samé). Dosaďme si c=1 a d=0 a počítejme:
{a,b} * {1,0} = {a,b}
Můžete si také sami ověřit, že součin dvou reálných čísel (tedy dvou bodů na ose x) bude podle tohoto pravidla opět reálné číslo (bod na ose x) a jeho hodnota bude součinem, který očekáváme.
{a,0} * {c,0} = {a*c,0}
Při pohledu na tu zapařenou definici součinu si možná říkáte, že ta reálná jednička by se možná dala zachránit nějak jinak. A v jistém smyslu máte pravdu. Smysluplný součin se v "číselné rovině" dá definovat i jinými způsoby (viz např. dvojná čísla). Výše uvedená definice ale odpovídá definici uvedené v algebraické části a tím nás dovede k jedné z nejpozoruhodnějších struktur celé matematiky - ke komplexním číslům.
Na tomto příkladu hezky vidíte, jak vlastně matematika funguje. Jejím posláním je nejen zkoumat stávající struktury a jejich výpočetní možnosti, ale také ty struktury rozšiřovat a zjišťovat za jakých podmínek poskytují výhody původního systému. Kdyby se matematika spokojila s tím, co fungovalo včera, dostala by se do pozice malých kluků, kteří se každou neděli cachtají v malé zátoce a vůbec netuší, že vůkol se rozkládá krásné velké jezero, skýtající nepoměrně více sportovních možností než původní zátoka.
(postbambule)
Když se na to teď podíváme z trochu vyšší perspektivy, dvojici čísel {a,b} si můžeme představovat buď jako bod v rovině, nebo jako dvourozměrný vektor a nebo jako komplexní číslo. Každý pohled má své pro i proti a záleží na tom, který aspekt zrovna upřednostňujeme.
Z praktického hlediska se bod od vektoru příliš neliší. Vektor není nic jiného než bod, který si svůj počátek nosí s sebou (jako šnek, který si s sebou vozí svůj domeček) a používá se hlavně tam, kde je potřeba mít pohyblivý souřadný systém (např. ve fyzice) a nebo kde budete dvojice čísel často sčítat (v lineární algebře). Všimněte si na obrázku nahoře, jak je pro potřeby součtu pohodlné, že si ten červený bod v nese svůj počátek s sebou, takže ho můžete "přiložit" k jinému bodu (tomu modrému) a vizuálně sečíst. Ta šipka nám vlastně umožňuje vidět daný bod vzhledem k jeho "přenosnému" počátku.
Pokud vás zajímá pouze geometrie, vystačíte si pravděpodobně s body a vektory můžete nechat plavat. Naopak, budete-li chtít kromě sčítání používat i ostatní aritmetické operace, komplexní čísla budou tím pravým ořechovým nástrojem. Dívejte se na ně jako na "chytré body" v rovině, které umí to samé co váš telefon. Počítat.
+++++++++
A teď to splácáme dohromady
Spojením obou přístupů si vytvoříme úplný obraz komplexních čísel.
Aby bylo jasné, jak spolu ty dva předložené pohledy souvisí, podívejme se, jak se bod {0,1} (což je jednička na ose y) chová při součinu. Vynásobíme ho se sebou samým a podle výše uvedeného pravidla pro násobení bodů dostaneme:
{0,1}2 = {0,1} * {0,1} = {-1,0}
Tak vida, tento bodík na druhou se rovná -1. Ta jednička na ose y tedy není nic jiného než ono mystické íčko zavřené ve sklepě pana Marečka! A jsme doma.
Zatímco osa x reprezentuje reálná čísla (de facto násobky jedničky), osa y reprezentuje čísla imaginární (násobky íčka). A to je ten chybějící článek, který spojuje algebraický a geometrický náhled. Komplexní číslo x+yi je jen jiné označení pro bod {x,y}, ke kterému se dostaneme tak, že popojdeme x dílků podél osy x a pak y dílků podél osy y. V praxi si komplexní čísla představujeme jako body {x,y} v rovině, ale pokud s nimi počítáme, zapisujeme je obvykle v algebraickém tvaru x+yi. Pak si nemusíme pamatovat tu zapařenou násobící formulku, ale součin provedeme přes dvojčleny (metodou FOIL).
Na tom obrázku vpravo jsem naznačil ještě jeden důležitý pojem. Komplexnímu číslu, které je k danému číslu z symetrické podle osy x se říká komplexně sdružené a značí se buď vodorovnou čárkou nad z a nebo hvězdičkou, tedy z*. Z geometrie je jasné, že číslo z* má stejnou souřadnici x a opačnou souřadnici y. Algebraicky to znamená, že pokud si označíme z = x+yi, tak dostaneme z* = x-yi. Význam čísel komplexně sdružených (tedy symetrických podle osy x) spočívá v tom, že jejich součet i součin je reálné číslo (a teď budu pro krát používat tečku).
z+z* = (x+yi) + (x-yi) = 2x
z . z* = (x+yi) . (x-yi) = x2 - xyi + xyi - y2 i2 = x2 + y2
Tuto vlastnost využíváme při dělení komplexních čísel (které vám stále dlužím).
(a+bi) / (c+di)
Vydělit dvě komplexní čísla znamená převést výše naznačený zlomek na základní algebraický tvar a od toho cíle nás dělí jen jedna maličkost: to íčko ve jmenovateli. Ze základní školy si ale vzpomeneme, že čitatel i jmenovatel zlomku můžeme vynásobit libovolným nenulovým číslem aniž by se změnila hodnota zlomku. A tak se toho íčka dole zbavíme tak, že zlomek pronásobíme číslem komplexně sdruženým ke jmenovateli (tím ze jmenovatele uděláme reálné číslo!) a se zbytkem si pak hravě poradíme. Tady je příklad:
(2+3i)/(1+2i) = (2+3i).(1-2i) / (1+2i).(1-2i) = (8-i) / 5 = (8/5) - (1/5)i
Všimněte si, že ten poslední výraz už je regulární algebraický tvar komplexního čísla (tj. reálné číslo plus jiné reálné číslo krát i). To že obě složky jsou zde zlomky by nás nemělo překvapit. Dostali jsme je přece jako výsledek určitého podílu.
A pro úplnost ještě komplexní odčítání - to se stejně jako sčítání provádí po složkách, takže to nic těžkého není (jen musíte dávat bacha na mínusy a závorky).
(-2+3i) - (1+5i) = - 3 - 2i
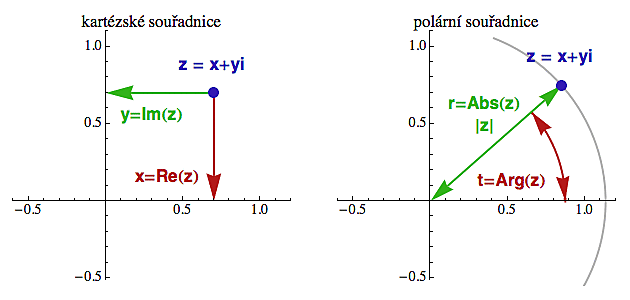
A závěrem ještě trocha terminologie. Protože komplexní čísla jsou v podstatě body v rovině, můžeme je popsat nejen standardními kartézskými souřadnicemi, ale také souřadnicemi polárními.
Ty kartézské souřadnice jsou přímo zakódované v algebraickém tvaru komplexního čísla (viz obrázek níže vlevo). Souřadnici x říkáme reálná část komplexního čísla z a značíme ji Re(z). Souřadnici y říkáme imaginární část komplexního čísla z a značíme ji Im(z). Bod na obrázku je 0.7 + 0.7i, takže jeho reálná i imaginární část je 0.7 (všimněte si, že íčko samo o sobě se do té imaginární části nezapočítává!).
Na obrázku vpravo si přikreslíme kružnici se středem v počátku, která naším komplexním číslem prochází (je naznačena šedě). Polární souřadnice čísla z jsou také dvě: jednak zelený poloměr této kružnice a jednak červený úhel sevřený bodem z v počátku (měřeno od kladné osy x). Tomu poloměru r se říká absolutní hodnota komplexního čísla z a značí se buď Abs(z) a nebo stejně jako pro reálná čísla |z|. Úhlu t říkáme argument komplexního čísla z a značíme ho Arg(z).
Pokud známe polární souřadnice (r,t) dostaneme ty kartézské z geometrie trojúhelníku:
x = r cos(t)
y = r sin(t)
Opačným směrem je to trochu komplikovanější. Pokud známe kartézské souřadnice {x,y}, dostaneme ty polární z Pythagorovy věty a z inverzní funkce tangens:
r = sqrt(x2+y2)
t = arctg(y/x), pro kladná x (pro záporná si s tím musíte trochu pohrát)
Bod na obrázku vpravo je z = 0.85 + 0.75i, takže jeho polární souřadnice jsou
Abs(z) = r = sqrt(0.852+0.752) = 1.13358
Arg(z) = t = arctg(0.75/0.85) = 0.722979 (radiánů - tj. cca 41.4 stupňů)
+++++++++
Možná si teď říkáte, kdy tahle rozšiřovací šílenost skončí. Co když narazíme na nějakou jinou rovnici, která nebude mít řešení ani v komplexních číslech a pak budeme muset náš systém opět horko těžko nastavovat.
Naštěstí se obáváte zbytečně. Základní věta algebry nám říká, že každá polynomiální rovnice (tedy taková, která obsahuje pouze přirozené mocniny x) s komplexními koeficienty se v komplexních číslech dá úplně vyřešit. Lineární, kvadratická, kubická a nebo jakákoliv vyšší. Matematici sice z dlouhé chvíle ještě pár exotických číselných systémů splichtili, ale to jsou už spíše jen kuriozitky. Matematika jako taková zůstává vystavěna na podloží komplexních čísel a hned tak se to asi nezmění.
Protože nejlepší způsob jak pochopit jakýkoliv komplexní problém je přečíst si o něm něco ze dvou různých zdrojů, můžete si jako rychlé opáčko přelouskat začátek wikipedie (až po oddíl "komplexní funkce")
+++++++++
Historická poznámka: Jedním z prvních vědců, kteří pro komplexní čísla našli použití v praktickém životě - a to celé dvě dekády před jejich vítězným tažením kvantovou mechanikou - byl český polyhistor a zanícený odmocňovatel záporných čísel, Jára Cimrman.
Při placení zlatavého moku v liptákovském hostinci se zhusta stávalo, že se Sirotkův závěrečný počet kousků dramaticky rozcházel s tím, co si pamatovali páni konzumenti. Proto se osazenstvo Cimrmanova stolu dohodlo s hospodským na kompromisním řešení. Ta piva, na kterých se obě strany shodly, se jmenovala reálná a platila pro ně plná cena. Naopak poloviční cena se platila za piva imaginární, která existovala pouze v Sirotkově hlavě a hosté se na ně za žádných okolností nemohli rozpomenout.
Můžeme být pyšní na to, že v době, "kdy komplexní čísla byla v západní Evropě postrachem horních deseti tisíc, u nás matematickým aparátem podivínů a v carském Rusku pouze předmětem vášnivých debat v anarchistických kroužcích" (abych parafrázoval samotného Mistra), hostinský Sirotek čmáral na pivní tácky tak složité komplexní výrazy, že se na ně jezdili dívat věhlasní učenci až z Drážďan.
+++++++++
Jako hudební doprovod pro minisérii o komplexních čísel jsem se rozhodl sáhnout po písničkách v jazyce, který považuji za mimořádně komplexní. A to je čeština. Takže si rozložte lehátko v zahradě a poslouchejte. Věra Špinarová: V zahradě rostě kmín.
Předchozí díly Matykání.
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
| Další články autora |
Tři roky vězení. Soud Ferimu potvrdil trest za znásilnění, odvolání zamítl
Městský soud v Praze potvrdil tříletý trest bývalému poslanci Dominiku Ferimu. Za znásilnění a...
Studentky rozrušila přednáška psycholožky, tři dívky skončily v nemocnici
Na kutnohorské střední škole zasahovali záchranáři kvůli skupině rozrušených studentek. Dívky...
Takhle se mě dotýkal jen gynekolog. Fanynky PSG si stěžují na obtěžování
Mnoho žen si po úterním fotbalovém utkání mezi PSG a Barcelonou postěžovalo na obtěžování ze strany...
Školu neznaly, myly se v potoce. Živořící děti v Hluboké vysvobodili až strážníci
Otřesný případ odhalili strážníci z Hluboké nad Vltavou na Českobudějovicku. Při jedné z kontrol...
Prezident Petr Pavel se zranil v obličeji při střelbě ve zbrojovce
Prezident Petr Pavel se při střelbě na střelnici v uherskobrodské České zbrojovce, kam zavítal...
USA a Čína musí být partnery, řekl Si. Blinken mu vyčetl podporu Ruska
Ve vztazích mezi Čínou a Spojenými státy zůstává mnoho problémů. Musí ale být spíše partnery než...
KOMENTÁŘ: Byrokracie s vízy? Přitvrdíme. Jak Česko zařízlo studenty z ciziny
Premium Nenápadná úřední klička zásadně zkomplikovala život zahraničních studentů v Česku. Stát ještě...
Podvodník prodával falešné vstupenky na koncerty i sport, naletělo mu 500 lidí
Falešné vstupenky na kulturní a sportovní akce nabízel na internetu muž z Uherskohradišťska, který...
V kontejneru vzplála stará elektrobaterie, patrně kvůli technické závadě
Zřejmě závada na staré elektrobaterii způsobila páteční požár kontejneru na skladování...

Specialista na controlling - HO, dovolená navíc #x4FEf
INDEX NOSLUŠ s.r.o.
Plzeňský kraj
nabízený plat:
40 000 - 50 000 Kč
- Počet článků 402
- Celková karma 19,54
- Průměrná čtenost 920x