Fraktály jsou živoucím dokladem, že komplexní čísla nejsou jen mechanickým rozšířením čísel reálných, ale že díky své dvojrozměrnosti přináší aspekty, které se na reálné přímce nasimulovat nedají. Striktně vzato k pochopení fraktálů nemusíte znát komplexní funkce - on se ten jejich výrobní postup dá obejít pomocí reálného zobrazení z roviny do roviny (což jsem v podstatě udělal v prvním díle tohoto cyklu). Nicméně když už jsem se v Matykání ponořil do základů komplexní analýzy, můžeme konečně pohlédnout pravdě do tváře: divé tvary fraktálů mají svůj základ v komplikované algebraické struktuře komplexních čísel. Stejně jako v reálném systému jsou jejich kostrou zlomky (když se podíváte třeba na Fordovy kružnice, tak v nich určitou příbuznost s fraktály naleznete). Jejich vzájemné vztahy jsou však podstatně bohatší a vytváří nekonečně komplikované útvary do jejichž hlubin se můžete - v rámci rozlišovacích schopností vašeho softvéru - nořit téměř bez omezení.
Dnes se nejprve podíváme na komplexní definici Mandelbrotovy množiny a potom vám ukážu několik ukázek pro funkce, které jsou trochu složitější než jednoduché mocniny z předcházejících dílů (většina obrázků Mandelbrotovy množiny na internetu je odvozena z kvadratické funkce).
Mandelbrotova množina (komplexně)
Kdykoliv vidíte obrázek Mandelbrotovy množiny, vidíte vlastně kousek komplexní roviny, jejíž body jsou obarveny podle chování jisté komplexní funkce F(z), která je každému bodu (a tedy pixelu) přiřazena.
To přiřazení je celkem jednoduché: nejprve si vezmeme libovolnou základní funkci f(z) - ta bude stejná pro všechny body budoucího obrázku - a pro každý komplexní bod s pak budeme zkoumat chování "posunuté" funkce F(z) = f(z)+s. Ta funkce F(z) už je samozřejmě jiná pro každý konkretní bod komplexní roviny. Pokud je tou základní funkcí kvadratická parabola f(z) = z², a tím "posunutím" třeba číslo s = 0,8+1,1i, pak jsme pixelu odpovídajícímu tomuto komplexnímu bodu přiřadili funkci F(z) = z²+0,8+1,1i.
Teď už se jenom musíme podívat, jak z chování té funkce F(z) vydundáme barvu příslušného pixelu.
+++++++++
Jak jsem naznačil v minulém Matykání, komplexní funkce F není nic jiného než skříňka s trpaslíkem, do které vhodíme vstupní komplexní číslo z a trpaslík nám z něj pak udělá nějaký komplexní výstup w = F(z). Fraktály jsou vytvořeny procesem, kterému se říká iterace funkce. Není to nic těžkého: do dané funkce (skříňky) vhodíme určité číslo a to, co nám trpaslík vyhodí na výstupu, vhodíme opět dovnitř a takhle to neustále opakujeme. Cokoliv z funkce na výstupu vypadne vhodíme okamžitě zpátky (vstupním otvorem).
To úplně první vhazované číslo si můžeme vybrat celkem libovolně (o tom více příště), ale typicky se za něj vybírá 0. Pokud tu posloupnost bodů, které postupně vhazujeme do trpaslíkovy skříňky chcete vidět explicitně, můžete si ji představit následující formulkou:
0, F(0), F(F(0)), F(F(F(0))), F(F(F(F(0)))), ....
(ten třetí bod není nic jiného než předchozí výstup znovuvhozený do funkce atd.)
Barvu daného pixelu teď odvodíme z chování této posloupnosti. Zhruba řečeno, pokud ta posloupnost odkráčí do nekonečna, pixel obarvíme barvou (z nějaké předem připravené tabulky barev), která odpovídá počtu kroků, které jsme k tomu potřebovali. Pokud ta posloupnost do nekonečna neodkráčí, to znamená, že se neustále "šmrdlá" poblíž počátku, pak daný pixel obarvíme černě.
A teď trochu přesněji. Protože počítač nezná pojem "odkráčet do nekonečna" a protože výraz "šmrdlat se poblíž počátku" nemá přesný matematický význam, vytyčíme si kolem počátku nějaký pevný a dostatečně velký kruh (obvykle stačí poloměr r=10, ale můžete zkusit i větší) a co bude vně kruhu, bude "v nekonečnu" a co bude uvnitř, bude "blízko počátku".
No a teď už je to barevné přiřazení jasné. Pokud naše posloupnost iterací vyběhne z kruhu během n-tého kroku, obarvíme pixel n-tou barvou z tabulky barev. Pokud z kruhu nikdy nevyběhne, pixel zůstane černý. V ilustracích níže používám tzv. barevné gradienty (aby se barvičky měnily hezky spojitě) - konkretně "TemperatureMap" ze softvéru Mathematica.
V úvodu této fraktální série jsem v souladu s konvencemi vzal za tu základní funkci f(z) = z², pak jsem ji rozšířil i na vyšší mocniny a dnes se podíváme, jak by Mandelbrotova množina vypadala pro komplikovanější komplexní funkce.
V ilustracích níže vám nejprve představím danou "základní" funkci, pak vám ukážu příslušnou Mandelbrotovu množinu vcelku a nakonec z ní udělám několik výřezů, aby bylo vidět, že jak zvětšujeme rozlišení, objevují se nové a nové detaily, často daleko krásnější než to, co bylo vidět ze začátku. Je to tak trochu jako když strčíte nohu mouchy pod mikroskop. Z toho co vypadalo jako nudná končetina je najednou hustý prales chloupků a výstupků. Fraktály jsou to samé. Abyste skutečně odhalili jejich krásu, musíte si udělat výřez a potom výřezy z výřezu a to tak dlouho, dokud vám to váš softvér umožní. Čím hlouběji proniknete, tím větší je šance, že narazíte na něco, co zatím žádné jiné oko nespatřilo.
+++++++++
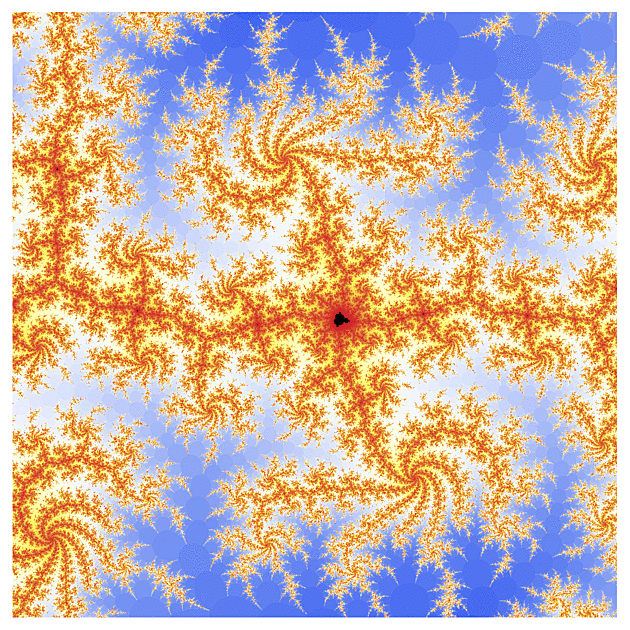
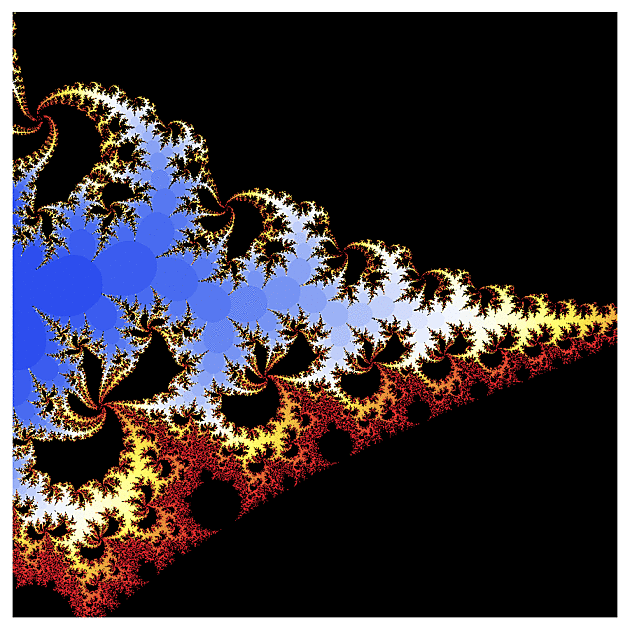
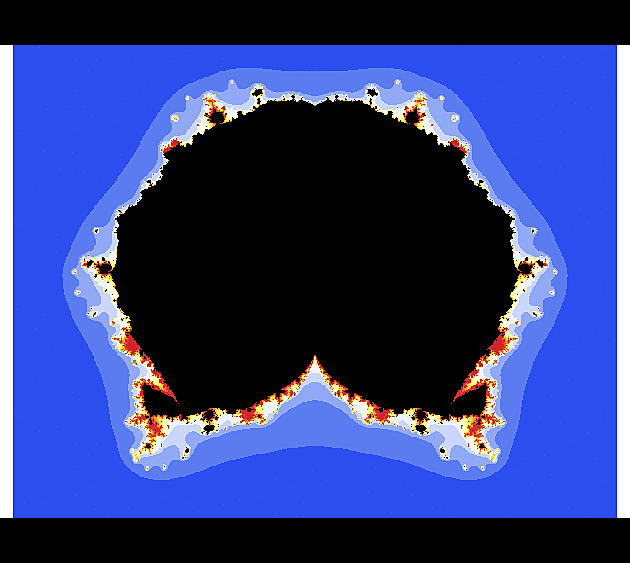
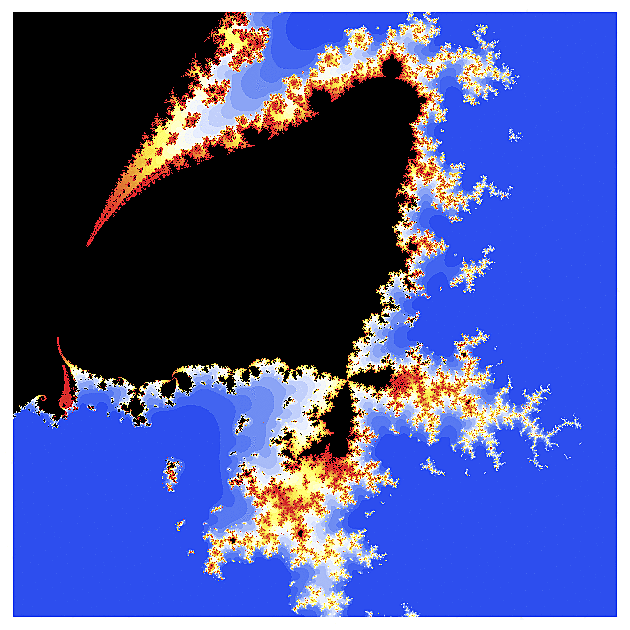
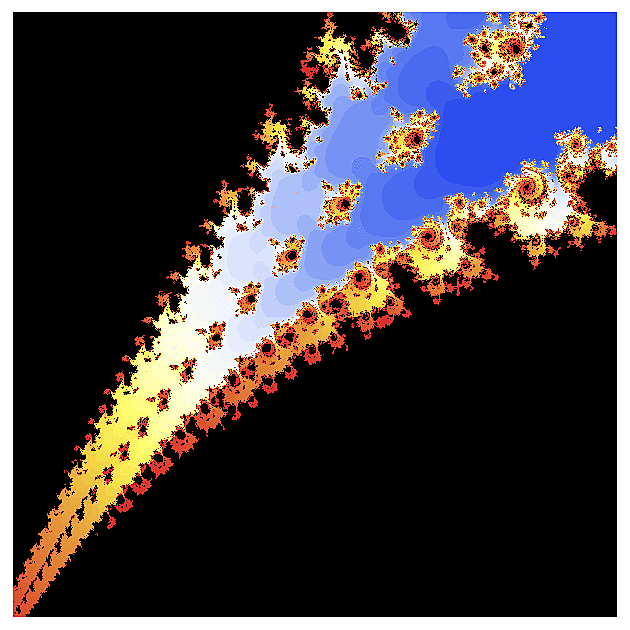
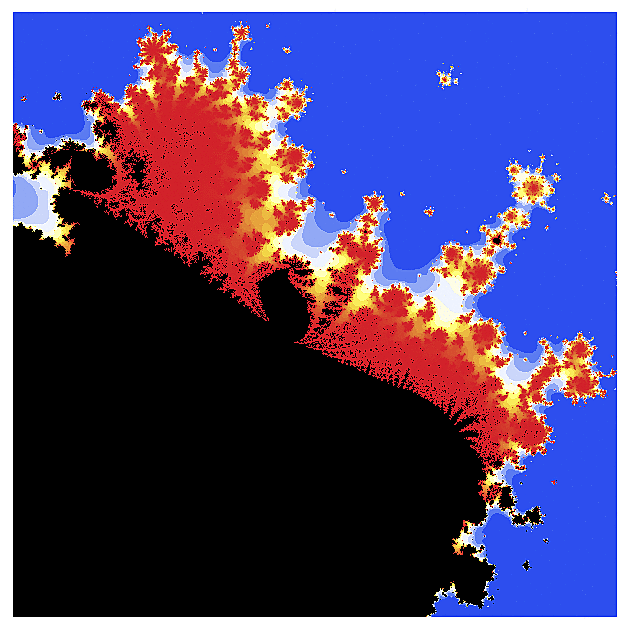
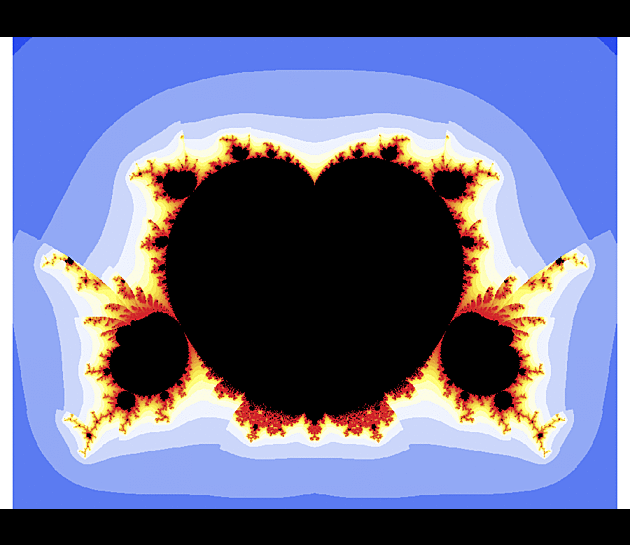
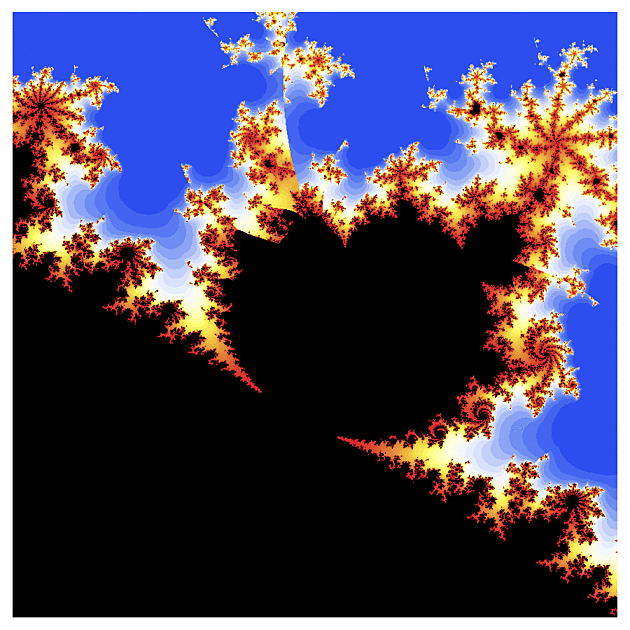
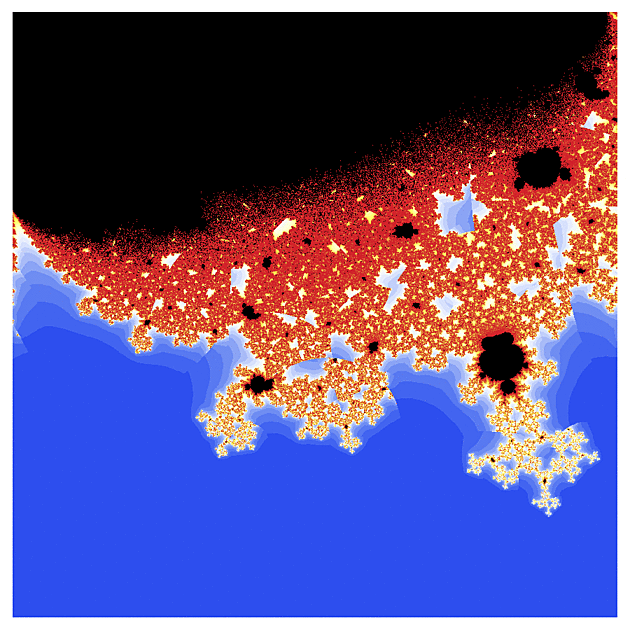
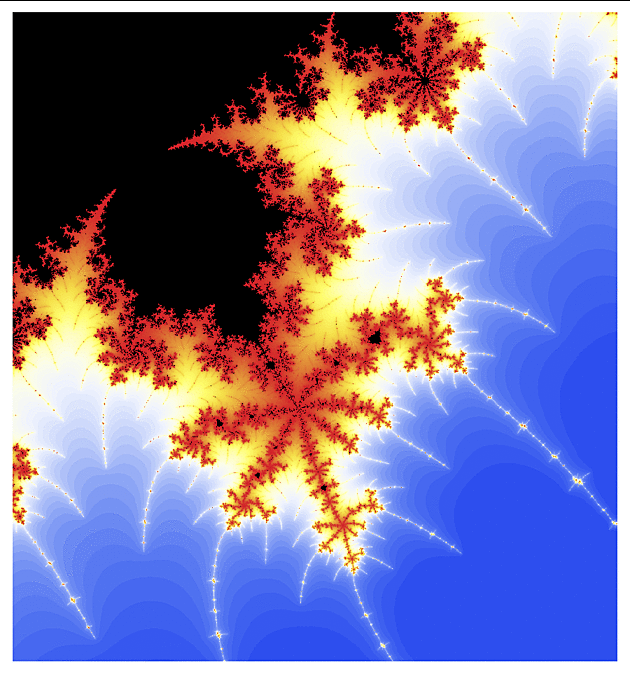
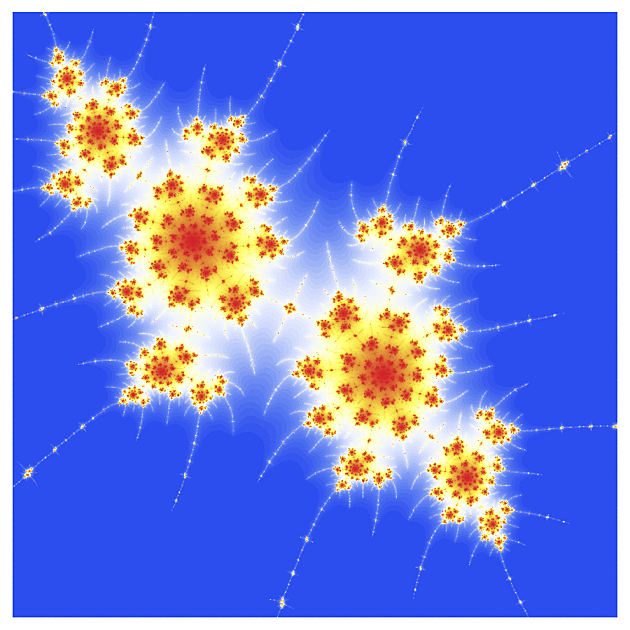
f(z) = exp(z)
Ten první obrázek vypadá pro znalce Mandelbrotovy množiny možná trochu nezvykle (přece jen exponenciela je podstatně komplikovanější než kvadratická funkce), ale jen co se začneme zaměřovat na detaily, nalezneme velmi podobné konfigurace jako u "kvadratické" Mandelbrotovy množiny. To rybí oko v úvodním obrázku je dáno volbou poloměru r a strmostí barevného gradientu a vhodným přenastavením se dá do jisté míry potlačit.
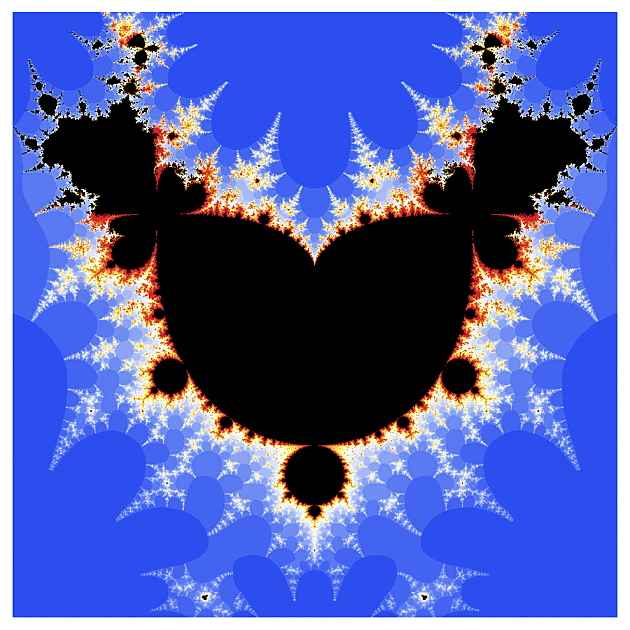
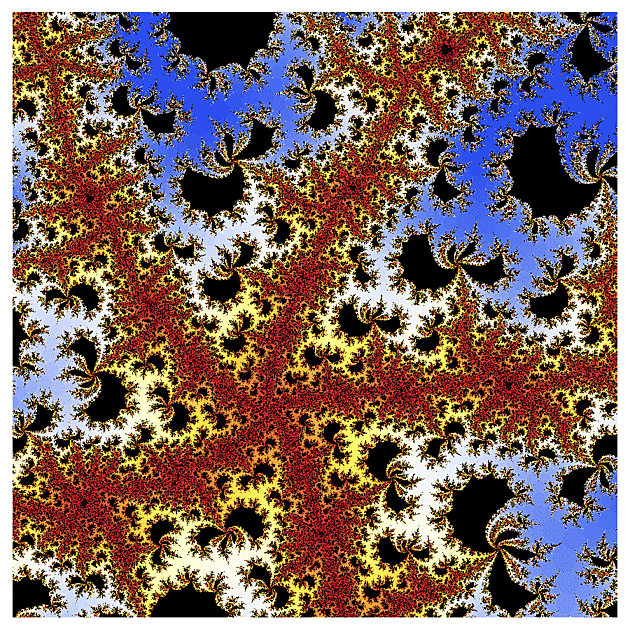
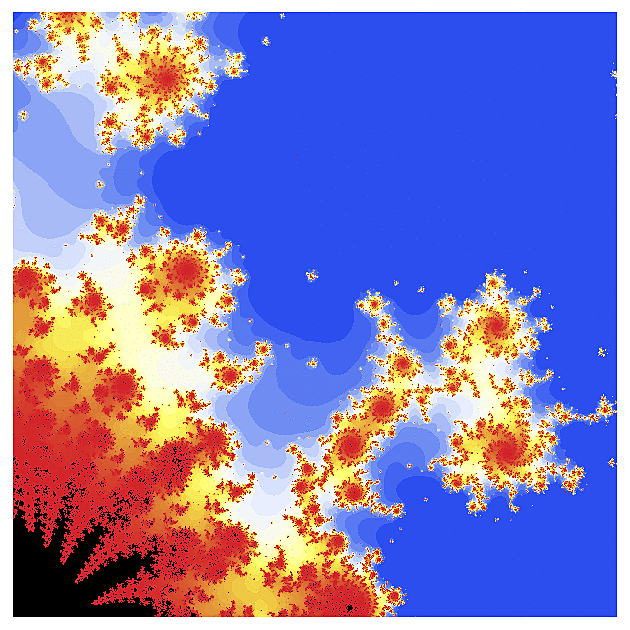
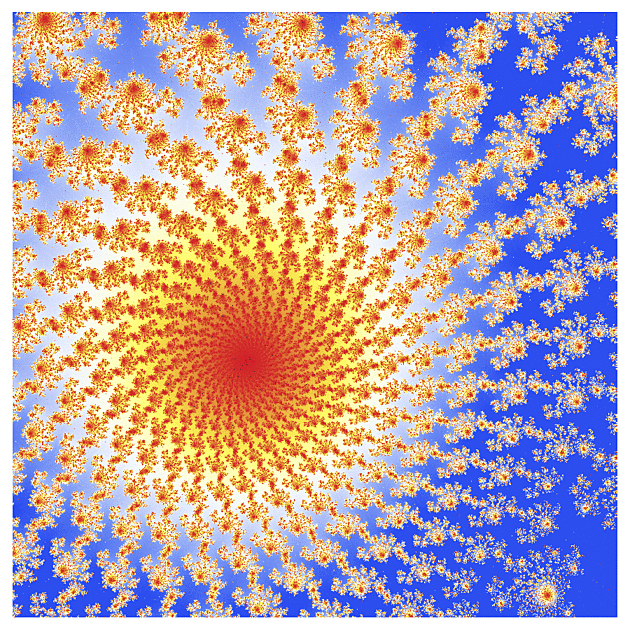
f(z) = arcsin(z)
Další funkcí na holení bude inverzní komplexní sínus (upravený tak, aby jeho Taylorův polynom začínal kvadratickým členem)
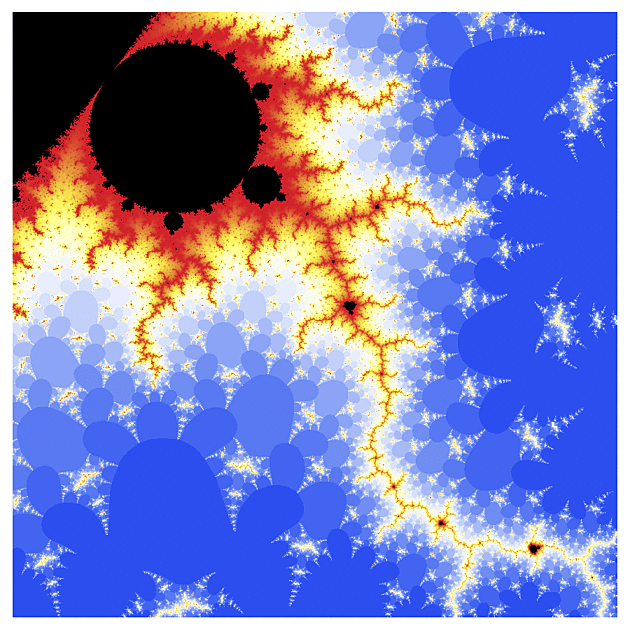
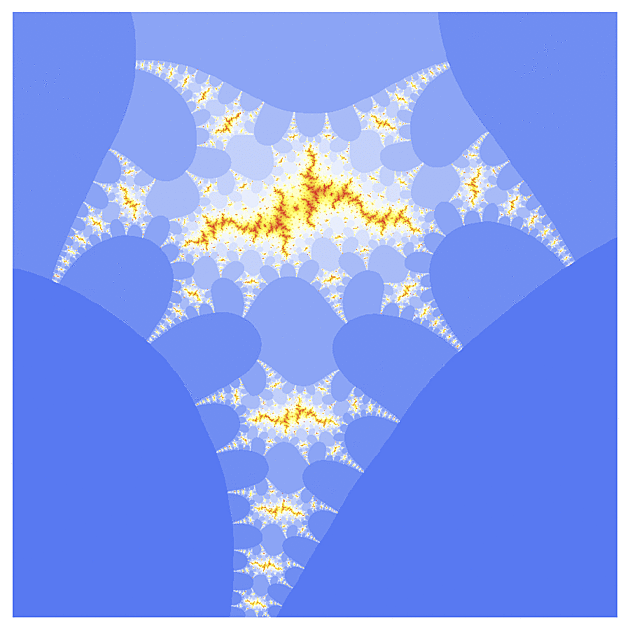
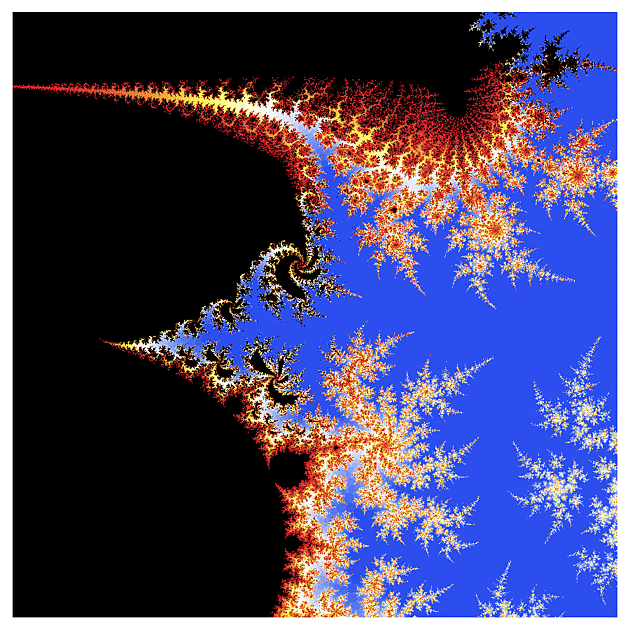
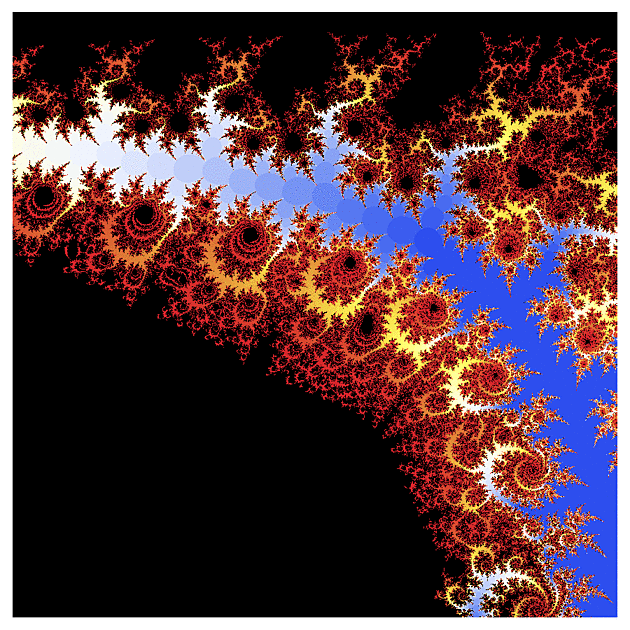
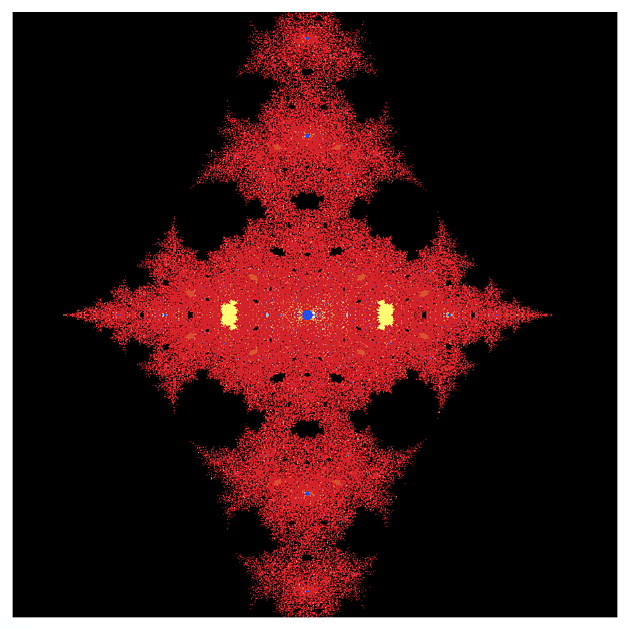
f(z) = cosh(z)
A teď něco z hyperbolického soudku: kosínus.
Ten vypadá už na první pohled trochu jinak, takže jsem postupně udělal několik výřezů z různých částí toho úvodního obrázku. U komplikovanějších funkcí ale musíte počítat s tím, že jejich výpočet není tak přesný jako u kvadratické funkce (obzvlášť u výřezů, kde se parametr s mění v řádu 0.00001), takže ty obrázky nejsou tak ostré jako u klasické Mandelbrotovy množiny.
a teď se mrkneme trochu jinam
a na závěr hyperbolického kosínu ještě nahlédneme semhle:
f(z) = gamma(z)
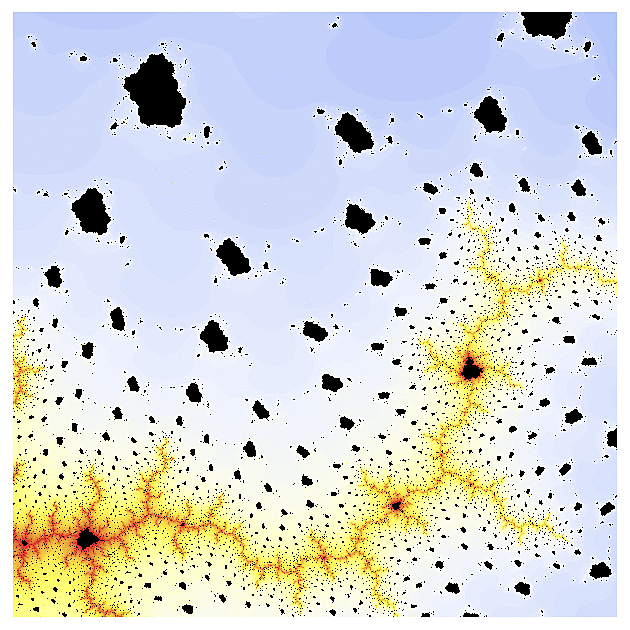
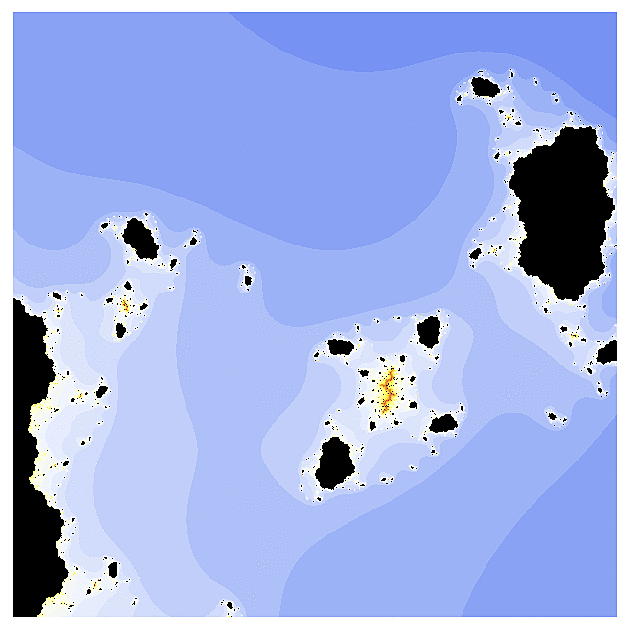
Poté, co se fraktály úspěšně popasovaly se síny a kosíny, vzal jsem si na paškál jednu z nejkomplikovanějších funkcí - tzv. gamma funkci. V jižní části příslušného fraktálu jsem nalezl kopie kvadratické Mandelbrotovy množiny, ovšem obklopené rojem asteroidů, které nezmizely ani když jsem přešel k výřezům (odkud se ty asteroidy berou netuším).
Poté jsem se přesunul do jihovýchodního výběžku, kde ty asteroidy zmizely, ale protože gamma funkce už je opravdu na výpočet docela komplikovaná, obrázky "vyřezané" z této oblasti postrádají propracovanost, jelikož počítač nedokáže chování pro jednotlivé hodnoty parametru s přesně odlišit.
a ani na severu úvodního obrázku jsem příliš krásy nenalezl
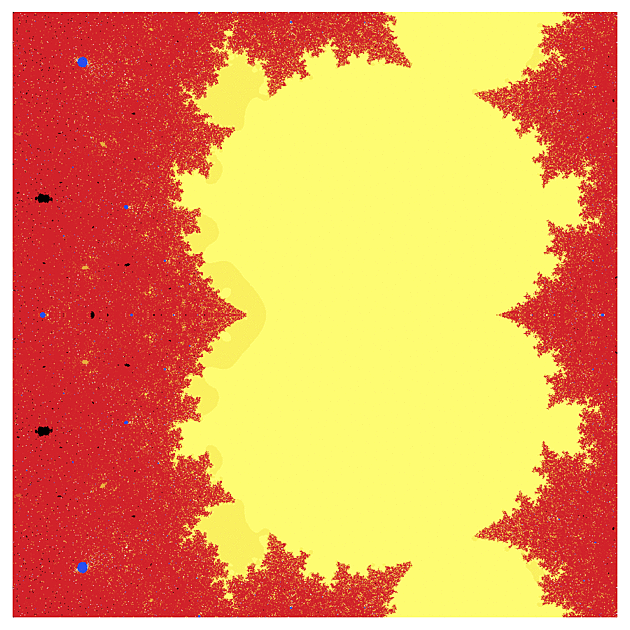
f(z) = tanh(z)
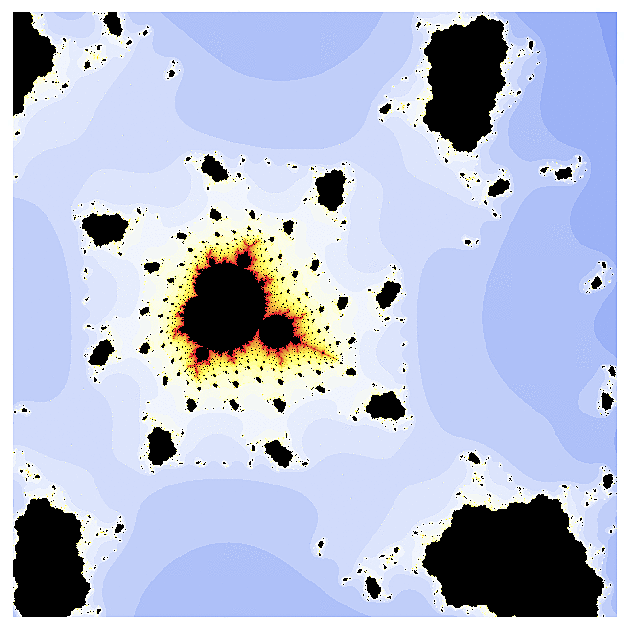
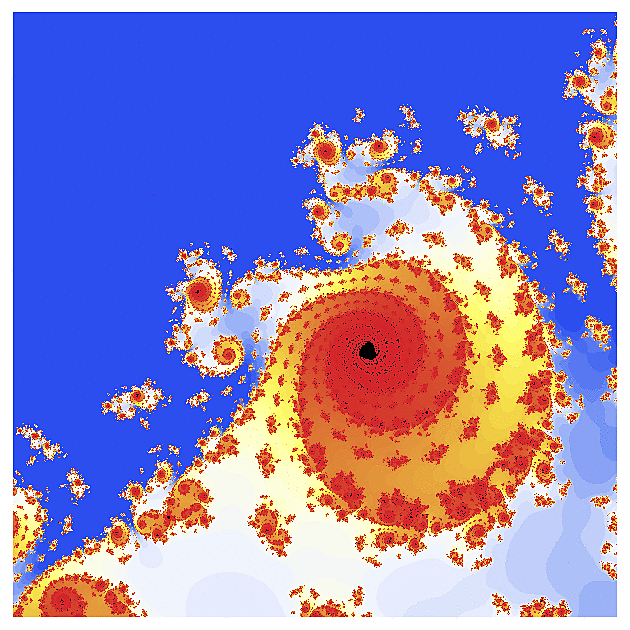
Ještě větší průšvih nastal, když jsem si vzal hyperbolický tangens. Tato funkce má v komplexní rovině spoustu pólů a její fraktál je v jistém smyslu inverzní. Zatímco klasická Mandelbrotova množina vypadá jako černé moře obklopené pevninou barev, zde jsem nalezl barevné moře v černé pevnině. Na druhém obrázku uvidíte detail té žluté skvrny.
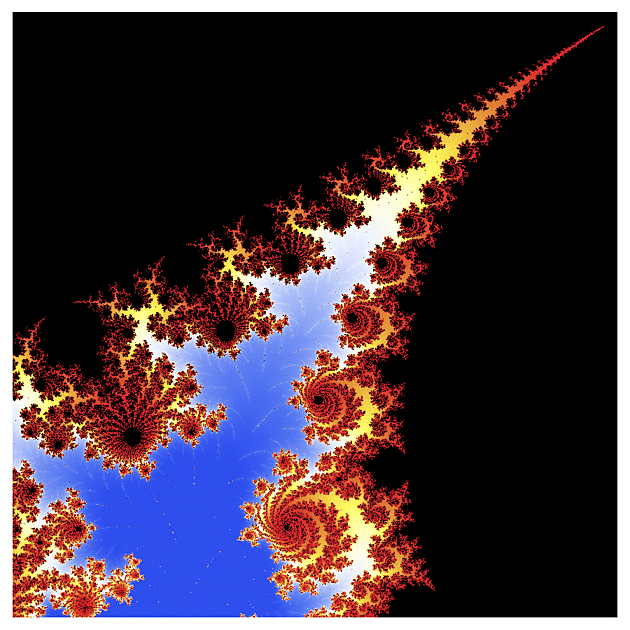
f(z) = sqrt(z)
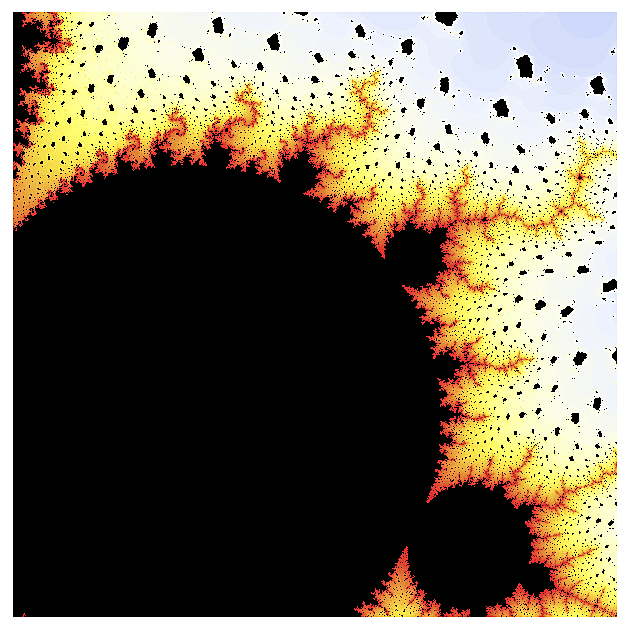
V minulém Matykání jsem se zmínil, že komplexní logaritmus má problém se spojitostí, který pak zdědí všechny funkce z něho odvozené - například druhá odmocnina. Při pohledu na fraktál z ní odvozený si můžete všimnout, že některé jeho oblasti jsou zalomené - asi tak jako když pozorujete tužku ve sklenici vody. To je právě způsobené tou nespojitostí v definici komplexního úhlu (a tedy i logaritmu a jeho odvozenin). V jižní části prvního obrázku vidíte, že ten fraktál je tam celý takový "rozsypaný" (detail této oblasti je na obrázku třetím).
f(z) = z²
A abychom se nerozloučili takovými ošklivými obrázky, dáme si na závěr pár výřezů z klasické (kvadratické) Mandelbrotovy množiny.
+++++++++
Předchozí díly série "Cesta do hlubin fraktálovy duše"
