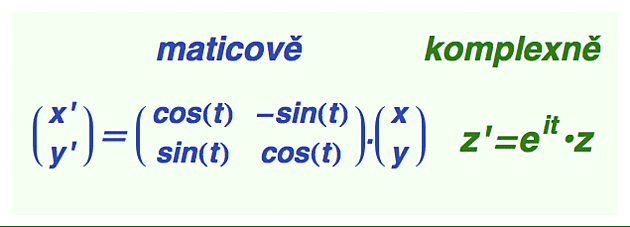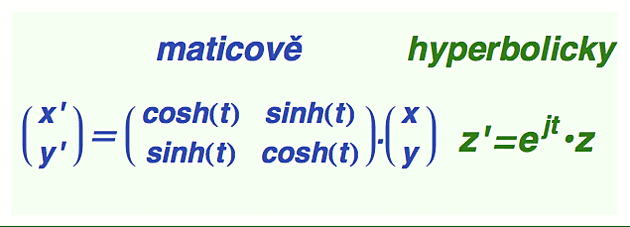Matykání: jak zatočit s virtuálním světem
V jedné staré čínské bajce se praví zhruba toto:
Moudrého muže navštíví chudý rolník a stěžuje si: "Mám malý domek a sotva se do něho s ženou a s 3 dětmi vejdeme. Co mám dělat?". Moudrý muž se zamyslí a posléze odvětí: "Přiber si do domku ještě kravku, osla, dvě kozy a čuníka a za měsíc mi přijď oznámit, jak se věci mají". Rolník se tedy vrátí domů, provede co mu moudrý muž poradil a za měsíc se hlásí s raportem: "Moudrý muži, tvá rada byla úplně bezcenná. Doma se prakticky nemůžeme hnout". Moudrý muž se usměje pod vousy a vece: "No a teď kravku, osla, dvě kozy i čuníka pošli zase do chlívku a uvidíš, jak se vám v domku bude krásně bydlet".
Pro ty z vás, kterým komplexní čísla stále připadají příliš komplikovaná mám dobrou zprávu. Dnes se seznámíme s kvaterniony - což jsou v jistém smyslu komplexní čísla složená ne z reálných, ale z komplexních čísel - a jsem přesvědčen, že po přečtení tohoto článku (a ne abyste ho spořádali na jedno posezení!) se ke komplexním číslům vrátíte se slzičkou v oku a budete je blahořečit pro jejich jednoduchost.
A protože kvaterniony se zhusta používají pro matematický popis a provedení rotací v 3D, podíváme se na problematiku otáčení trochu podrobněji. Zjistíme, že rotace v jistém smyslu odpovídají násobení komplikovanějších algebraických objektů. U rotací kolem souřadných os si celkem lehce vystačíme s maticemi. Pro obecné rotace jsou ale kvaterniony vítanou pomůckou a ta se nám ve virtuálním světě plném nečekaných nástrah může sakra hodit.
Pokud na nás ve vystříleném skladišti mírně radioaktivní břečky vyběhne zpoza zříceného nosníku dvouhlavá krvežíznivá nestvůra, těžko na ni můžeme s omluvným úsměvem volat: "Jé, prosimvás, nemohla byste se na mě vyřítit trochu víc zleva - já totiž umím otáčet zorným polem pouze kolem souřadnicových os."
To by se obluda mohla naštvat a ukousnout nám nezanedbatelný kus hlavy.
+++++++++
2D rotace
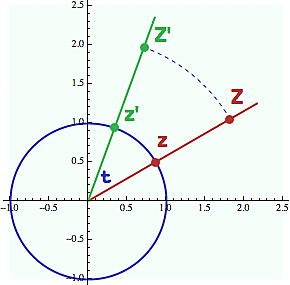
Rotace je operace důvěrně známá všem dobrodruhům, kteří se v mládí odvážili vyškrábat se na kolotoč. Z matematického pohledu je rotace určitým typem funkce, pouze s tím rozdílem, že vstup a výstup není číslo, ale bod v rovině (popřípadě v prostoru). Často je dobré si takové body představit jako vektory (tedy šipčičky posazené v počátku a směřující k danému bodu). Na vstupu zadáme vybraný bod (vektor) a rotace jej pootočí (obvykle kolem počátku) o předem stanovenou hodnotu úhlu t.
Takovým funkcím říkáme transformace, protože v jistém smyslu transformují rovinu (popřípadě prostor) pokud je aplikujeme na všechny body současně. Rotace má navíc tu vlastnost, že nemění vzdálenosti mezi body. Pokud si vezmeme dva body, např. z a Z, a pomocí rotace je otočíme řekněme o 40 stupňů, tak po provedené transformaci bude vzdálenost jejich obrazů z' a Z' stejná. Takovým transformacím říkáme isometrie (shodná zobrazení). K nejznámějším příkladům kromě rotace patří posunutí (translace) a zrcadlení (osová souměrnost neboli symetrie podle přímky).
Než se posuneme dále, je dobré si uvědomit následující triviální skutečnost: rotace kolem počátku je beze zbytku určena svým chováním na jednotkové kružnici (to se nám bude hodit při zobecňování). Jakmile víte, co dělá rotace s body na jednotkové kružnici, víte co dělá se všemi ostatními (ty v podstatě rotují podle svých "vzorů" na kružnici). Představme si rotaci naznačenou na obrázku vpravo. Její akce na kružnici odpovídá otočení o 40°. Všechny ostatní body roviny se dají na kružnici promítnout tak, že je vydělíte délkou příslušného vektoru (vzdálenost bodu od počátku). Jakmile stáhnete bod Z do bodu z na kružnici, můžete ho pootočit do bodu z' a pak ho vynásobit stejným číslem a uvést do konečné polohy Z'.
Komplexní čísla jsou mimořádně vhodným nástrojem pro popis 2D rotace, protože jejich polární forma z = r*exp(is) obsahuje úhel s (měřený v počátku) přímo ve své definici. Pokud chceme otočit nějaké takové číslo z o úhel t, vynásobíme ho prostě komplexní jednotkou exp(it), která ponechá polární rádius r beze změny a k polárnímu úhlu s přičte t. Kartézské souřadnice pootočeného bodu pak dostaneme obvyklým způsobem z polárního vyjádření r*exp(i(s+t)).
Pokud jste si na komplexní čísla vypěstovali alergii, nemusíte propadat beznaději. Pro popis 2D rotace můžete stejně dobře použít tzv. rotační matice (viz levá část dalšího obrázku). Namísto komplexního čísla z=x+iy si daný bod napíšete v souřadnicích {x,y} jako vektor a zleva jej vynásobíte uvedenou maticí. Můžete si sami zkusit, že výsledný bod bude - pro daný úhel t - stejný jako pootočené komplexní číslo.
Ta komplexní forma je o trochu kompaktnější a jakmile si zvyknete na formalismus komplexních čísel, lépe se pamatuje. Nicméně pokud vás zajímají pouze 2D rotace, můžete používat maticový pohled a netrápit se s tím zpropadeným íčkem. Komplexní čísla jsou důležitá hlavně pro své analytické vlastnosti a používat je pouze pro občasnou rotaci je jako kupovat si auto jen proto, že si tu a tam chcete poslechnout rádio.
A než se rozloučíme s komplexními čísly, ještě malou poznámku o skalárech a vektorech. V první aproximaci platí, že skaláry jsou čísla a vektory jsou n-tice čísel. To je z pohledu komplexních čísel trochu zavádějící, protože jsou to čísla, která mají sama o sobě vnitřní strukturu (jsou to de facto dvojice reálných čísel). Přesto bych vám doporučil se na komplexní čísla dívat jako na skaláry, protože ve fyzice se občas vyskutují i komplexní vektory (tedy n-tice komplexních čísel). Jen je třeba dávat pozor na dimenzi - ta závisí na tom, zda jsou vaše vektory reálné nebo komplexní (a tato informace by měla být součástí zadání problému, pokud se nedá vyvodit z kontextu). Trojice komplexních čísel mají (komplexní) dimenzi tři, přestože odpovídají šesticím reálných čísel (a mají tedy reálnou dimensi 6). Naštěstí se běžný smrtelník s komplexními vektory jen tak nesetká, takže si s tímto paradoxem nemusíte moc lámat hlavu.
+++++++++
Sekce jauvajs: Hyperbolická rotace
(tuto sekci možno přeskočit, obzvlášť pokud nefandíte teorii relativity)
Matematici trpí neodolatelným nutkáním věci zevšeobecnovat - jakmile objeví řekněme recept na borůvkový koláč a skutečně se jim podaří ho upéci, první co udělají je, že do dalšího těsta začnou cpát maliny, třešně, rozinky, křupky, kaštany, skleněnky nebo dokonce kousky cihel a při tom budou pozorovat, z čeho vznikají užitečné struktury a z čeho ne.
A tak se i stalo, že jednou takhle v neděli odpoledne nějakého vyšinutého algebraika napadlo, co by se asi tak stalo, kdybychom si vzali komplexní čísla - tak jak je známe - a tu imaginární jednotku, splňující i2=-1, nahradili číslem j, splňujícím j2=+1 (to jéčko sice posadíme na osu y, ale nebude to ani tak imaginární jednotka jako spíš druhá kopie jedničky, dvojná jednotka). Všechno ostatní zůstane stejné.
Dostaneme opět rovinu čísel, v níž bude každý bod {a,b} odpovídat algebraickému výrazu
z = a + bj
Takto vzniklým číslům se říká dvojná čísla (někdy též hyperbolická čísla) a počítá se s nimi úplně stejně jako s komplexními čísly, jen musíte mít na paměti, že j2=+1. To je důležité zejména pro (hyperbolické) násobení.
(3+7j) . (4-j) = 12 - 7j2 +28j -3j = 5 + 25j
I jednička 1+0j se chová, jak se sluší a patří
(3+5j) (1+0j) = 3+5j
Sčítání je po složkách a nepředstavuje žádnou obtíž:
(3 + 8j) + (-1-j) = 2 + 7j
Jakmile zvládneme základní aritmetické operace - sčítání a násobení - můžeme přikročit k definici svatého grálu matematické analýzy, tedy exponenciální funkce. Stejně jako pro komplexní čísla zde platí exp(s+tj) = exp(s)*exp(jt), takže nám stačí stačí definovat exponencielu pro násobek dvojné jednotky j. To se opět provede pomocí mocninných řad a výsledkem je formulka
exp(jt) = cosh(t) + j*sinh(t)
která nápadně připomíná Eulerovu slavnou identitu
exp(it) = cos(t) + i*sin(t)
To samozřejmě není náhoda. To, co je pro komplexní čísla kružnice, je pro dvojná čísla hyperbola. Pokud zvětšujete hodnotu parametru t, tak výraz exp(it) reprezentuje bod obíhající po jednotkové kružnici, zatímco bod exp(jt) probíhá jednotkovou hyperbolu a odpovídá její standardní parametrizaci (viz obrázek vpravo).
Parametr t odpovídá v obou případech dvojnásobku vystínované plochy (což u kružnice sice odpovídá naznačenému úhlu - ale pozor, u hyperboly už úhlu nedpovídá). Pro zadané t si souřadnice toho oranžového bodu spočítáte lehce. Naopak je to trochu těžší - musíte použít inverzní gonometrické či hyperbolické funkce. Například bod {5/3,4/3} leží na jednotkové hyperbole, protože splňuje její rovnici. Abychom zjistili jaké hodnotě parametru odpovídá, musíme vyřešit rovnici cosh(t)=5/3 a to znamená, že t bude inverzní hyperbolický kosínus: t = ArcCosh(5/3)=1.09861.
V kostce by se dalo říci, že zatímco běžná rotace posune ten oranžový bod (vlevo) podél kružnice o nějakou konstantní hodnotu parametru t, hyperbolická rotace posouvá oranžový bod (vpravo) podél hyperboly, na které leží, a taktéž o konstantní hodnotu t. To znamená, že všechny body se posunou podél svých hyperbol tak, že ta vystínovaná plocha vzroste o konstantní hodnotu. Ve zbytku této sekce se v tom trochu algebraicky porejpám a pokud to není váš šálek čaje, můžete to vypustit.
+++++++++
Tu analogii s komplexními čísly můžeme dále rozvinout. Pro dané číslo z = a + bj definujeme číslo dvojně sdružené (nebo též hyperbolicky konjugované) takto:
z* = a - bj
Absolutní hodnotu duálního čísla z (neboli jeho "velikost") teď můžeme definovat stejně jako v komplexním případě odmocninou ze součinu daného čísla z s jeho sdruženým protějškem z* (abych se s tou odmocninou nemusel tahat, napíšu ten vzoreček pro čtverec)
|z|2 = z.z* = (a+bj) . (a-bj) = a2 - b2
To znamená, že hyperbolická "velikost" čísla 3+2j bude
| 3+2j | = sqrt(5)
Na tuto veličinu se můžete dívat buď jako na "hyperbolickou" vzdálenost bodu x+yj od počátku a nebo jako na "hyperbolickou" délku odpovídajícího vektoru (na obrázku výše fialově). Ovšem není to žádná legrace - budete se muset vzdát své eukleidovské intuice o tom, co je to vlastně "délka" vektoru resp. "vzdálenost" bodu od počátku.
V komplexní analýze se ničeho vzdávat nemusíte - tam je absolutní hodnota totožná s eukleidovskou vzdáleností (odmocnina ze součtu čtverců), takže ten oranžový bod obíhající podél kružnice (vlevo) má skutečně stále stejnou "optickou vzdálenost" od počátku. Na hyperbolickou absolutní hodnotu je třeba si zvyknout. V pravé části obrázku se zdá, že oranžový bod se od počátku vzdaluje (pokud zvětšujeme parametr t). To je ale proto, že se na jeho vzdálenost podvědomě díváme eukleidovsky. Pokud přijmeme jako definici délky výše popsanou absolutní hodnotu, pak musíme konstatovat, že duální vzdálenost od počátku je stále stejná. Technicky to vyplývá z toho, že hyperbolické funkce splňují rovnici hyperboly (na obrázku v černém), zatímco goniometrické funkce splňují rovnici kružnice.
Kdo ví, jak se měří délky v prostoročasu už tuší o jakou čertovinu se jedná. Pokud si představíme jednorozměrný model prostoročasu se souřadnicemi {t,x}, pak je hyperbolická absolutní hodnota to, čemu se v teorii relativity říká interval. Jen je tam místo x trojice čísel {x,y,z}. Princip je ale stejný - prostoročas je hyperbolická struktura (tzv. Minkowského prostor).
Zda pohlížíte na rovinu jako na komplexní čísla a nebo na dvojná (hyperbolická) čísla záleží na vás a na tom, co se snažíte spočítat. Oba systémy představují platné rozšíření reálných čísel (s trochu jinými algebraickými vlastnostmi). Na každý bod {a,b} se tedy můžete dívat buď jako na komplexní číslo a+bi a nebo na dvojné číslo a+bj.
+++++++++
V každém případě je zajímavé, že i hyperbolická absolutní hodnota je kompatibilní s hyperbolickým součinem v tom smyslu, že absolutní hodnota součinu je součin absolutních hodnot - to vyplývá z hyperbolické verze Fibonacciho rovnice (formálně připomínající originální verzi)
(a2-b2) . (c2-d2) = (ac+bd)2 - (ad+bc)2
která reprezentuje čtverce absolutních hodnot součinu
(a+bj) . (c+dj) = (ac+bd) + (ad+bc) j
Můžeme si to zkusit pro konkretní čísla
(3+2j) . (4-j) = 10 + 5j
absolutní hodnota napravo je sqrt(75), zatímco pro členy nalevo se rovná sqrt(5) a sqrt(15). Součin posledně jmenovaných nám dá skutečně hodnotu sqrt(75).
+++++++++
Další užitečnou vychytávkou je polární forma. Každé číslo v komplexní rovině je charakterizované svou absolutní hodnotou r a velikostí parametru t a stejně to funguje i pro hyperbolická čísla.
Například číslo 3+2j má absolutní hodnotu sqrt(5) a hyperbolický parametr t = ArcCosh(3)=1.76275. Číslům, která mají (hyperbolickou) absolutní hodnotu 1 říkáme hyperbolické jednotky (např. o a c na obrázku) a protože leží na jednotkové hyperbole musí mít tvar exp(jt), pro nějakou hodnotu t.
To nás přivádí k myšlence hyperbolické rotace (vynásobíme dané číslo hyperbolickou jednotkou, která nechá absolutní hodnotu nezměněnou a parametr posune o nějakou konstantní hodnotu):
z' = exp(jt).z
(zde "krát" je hyperbolický součin)
Tato transformace tedy zvolený bod "posune" podél hyperboly, na které leží (tak jako normální rotace posunuje bod podél kružnice na které leží).
Pokud duální číslo z = r.exp(js) vynásobíme jednotkovým číslem c = exp(jt), dostaneme číslo
z' = r.exp(j(t+s))
Bod z' tedy vznikne z bodu z posunutím podél příslušné hyperboly (červené) o hodnotu parametru t - ta definuje intenzitu hyperbolické rotace stejně jako daný úhel t definuje intenzitu rotace klasické (a nezapomeňte, že pro hyperbolickou rotaci je parametr t ta vystínovaná plocha, nikoliv úhel).
To, že hyperbolická rotace navýší hodnotu parametru o konstantní hodnotu t je z té exponenciely vidět přímo (plyne to také ze součtových vzorců pro hyperbolické funkce). Opravdoví masochisté se ovšem mohou pokusit vytlouct to výpočtem z kartézských souřadnic (které jsou běžnému smrtelníkovi bližší).
Ale bude to bolet.
Vezměme si hyperbolickou rotaci na obrázku, která odpovídá jednotkovému bodu c = (5/3) + j (4/3). Odpovídající hodnotu parametru t jsme si spočítali výše: t=1.09861, takže c = exp(1.09861j). Ověřte si, že bod c skutečně splňuje rovnici jednotkové hyperboly. Bod, který hyperbolicky "otočíme", bude mít kartézské souřadnice z = (5/2)+(3/2)j. Tento bod leží na "dvojkové" hyperbole: x2-y2=22 (červená), jejíž parametrizace je {2*cosh(s),2*sinh(s)}. Hodnota jeho parametru je s=ArcCosh(5/4) = 0.693147. Těch 5/4 je polovina x-ové souřadnice 5/2 (protože v parametrizaci je 2 navíc).
Hyperbolické otočení provedeme tak, že bod z vynásobíme jednotkovým hyperbolickým číslem c:
z' = c.z = ((5/3)+j(4/3)).((5/2)+(3/2)j) = (1/6).(5+4j).(5+3j) = ...
... = (1/6).(25+20j+15j+12j) = (1/6).(37+35j)
(tu šestinu jsem dostal tak, že z prvního členu jsem vytknul třetinu a z druhého polovinu, abych se nemusel furt tahat s "těma zlomkama")
takže výsledek hyperbolického otočení je z' = 37/6 + 35/6 j
Lehce si ověříte, že z' leží na té samé červené hyperbole (rozdíl čtverců jeho souřadnic je také 22), a když si spočítáte jeho parametr (a x-ovou souřadnici musíme opět vydělit dvojkou, protože stále sedíme na té "dvojkové" hyperbole), dostaneme s' = ArcCosh(37/12) = 1.79176. A teď přijde kouzlo nejkouzlovatější. Ten parametr s' nového bodu není nic jiného než parametr starého bodu s plus rotační parametr t. Takže jsme si ověřili, že vše funguje tak, jak očekáváme: hyperbolická rotace vezme rotovaný bod a a posune ho podél dané hyperboly tak, že k jeho hyperbolickému parametru s přičte určitou konstantní hodnotu t - přesně jako je tomu u běžné rotace s úhly.
+++++++++
Pokud vám tento typ výpočtu není po chuti, nemusíte zoufat. Opět platí, že kdo potřebuje pouze tu a tam hyperbolicky zarotovat, nemusí se s algebraickou strukturou dvojných (hyperbolických) čísel vůbec obtěžovat, protože ta hyperbolická rotace se dá udělat i maticově.
Já vím, teď si asi říkáte, že tahle transformace je taková šílenost, že je vyloučeno, aby se něco takového vyskytovalo ve volné přírodě. Ale pámbů je jiného mínění. Lorentzova transformace ze speciální teorie relativity, která nám ukazuje jak se prostoročasové souřadnice mění při přechodu z jedné inerciální soustavy do druhé, není ničím jiným než hyperbolickou rotací - s tím, že intenzita rotace, tedy velikost toho rotačního parametru t, je dána vzájemnou rychlostí obou soustav (viz zde).
Jiný způsob visualizace normální a hyperbolické rotace je graf, který nám ukáže, co tyto dvě transformace provádí s jednotkovými vektory podél souřadných os. Označíme si je písmenky u a v a provedeme s nimi rotaci (vlevo) a hyperbolickou rotaci (vpravo).
Vidíte, že ta normální rotace prostě oba vektory otočí (a při tom samozřejmě zachovává jejich "standardní" délku definovanou komplexní absolutní hodnotou). Hyperbolická rotace ty vektory jen jakoby "stlačí" a opticky je prodlouží. Ve skutečnosti jsou ale ty zelené vektory napravo stejně dlouhé jako ty červené - ovšem za předpokladu, že je poměřujete hyperbolickou absolutní hodnotou. Také si všimněte, že při běžné rotaci od u k u' se špička vektoru posunuje po kružnici. U hyperbolické rotace se ta špička pohybuje po hyperbole.
Závěrem této sekce ještě malou poznámku.
To že jsme na "imaginární" osu umístili kopii jedničky j vlastně znamená, že na dvojné číslo 2+3j se můžeme dívat jako na obyčejnou pětku (2+3), s tím, že to číslo si pamatuje, jak bylo "rozštípnuto". Proto se v angličtině těmto číslům říká split-complex numbers (doslova "rozštípnutá").
A funguje to i pro hyperbolickou exponencielu
exp(jt) = cosh(t) + j*sinh(t)
pokud si "drze" dosadíte j=1, dostanete klasickou identitu
exp(t) = cosh(t) + sinh(t)
která je vidět ihned z definice hyperbolických funkcí.
Důvod, proč jste o duálních číslech asi ještě neslyšeli spočívá v některých jejich "nevhodných" vlastnostech. Inu, ne každá abstraktní konstrukce se setká s takovým spektakulárním úspěchem jako komplexní čísla.
Podívejte se například na tuto rovnici:
(1+j) . (1-j) = 1 - j2 + j - j = 0
Součin dvou nenulových čísel je roven nule (to se v reálných ani komplexních číslech stát nemůže). Takovýmto patologickým exemplářům říkáme dělitelé nuly a moc rádi je v matematice nevidíme (podrývají například tento klasický argument: pokud je součin dvou čísel nula, je alespoň jeden z faktorů roven nule)
A také z pohledu topologie jsou dvojná čísla "nežádoucí". Velká část analýzy je postavená na pojmu blízkosti dvou bodů. V komplexních číslech jsou body s jednotkovou vzdáleností od počátku na jednotkové kružnici a to vcelku odpovídá našemu intuitivnímu chápání blízkosti. U dvojných čísel ovšem body s jednotkovou "vzdáleností" od počátku leží na jednotkové hyperbole a to znamená, že i ty, které se nám jeví "šíleně daleko" (na konci každé větve) se stále nalézají "v okolí" počátku. A taková představa už vyžaduje opravdu silný žaludek.
Přesto se tu a tam naleznou nadšenci, kteří se pokouší z dvojných (hyperbolických) čísel vybudovat analýzu podobnou té komplexní (viz zde nebo zde).
+++++++++
Kvaterniony
Zhruba v polovině 19. století se ukázalo, že komplexní čísla nemusí být jen "předmětem vášnivých debat v anarchistických kroužcích", jak by řekl Jára Cimrman, ale že mohou poskytnout i dosud netušené nástroje pro matematickou analýzu. To samozřejmě ponouklo různé podnikavce k tomu, aby začali hledat rozšíření reálných čísel do 3D prostoru. Tedy pokusit se najít obdobu komplexních čísel ve tvaru:
{a,b,c} = a+bi+cj
(zda si takové číslo představujete jako abstraktní trojici, nebo na to půjdete přes algebraický zápis pomocí "imaginárních jednotek" i a j je vcelku na vás)
Součet po složkách nepředstavuje ani tady žádný problém a tak se celá záležitost brzy zredukovala na nalezení vhodné definice součinu. Takováto čísla jsou defacto 3D vektory (tedy body z 3D prostoru) a vhodný kandidát se zde nabízí v podobě vektorového součinu. Ale takový součin bohužel nebude splňovat základní vlastnost jedničky (tedy, že cokoliv krát jedna je to samé). Podívejme se na to:
{a,b,c} x {1,0,0}
Na jedné straně bychom chtěli, aby toto byl opět vektor {a,b,c}, ale na druhé straně je vektorový součin kolmý na oba součinitele a kýžený výsledek {a,b,c} bude těžko kolmý sám na sebe. Takže tudy cesta nevede.
(později se ukázalo, že problémy s 3D jsou nepřekonatelné a žádná matematická struktura, která by mohla reprezentovat třírozměrné "skaláry" neexistuje)
Nicméně tehdejší matematici věřili, že nějak se ten součin definovat dá a nadále do trojrozměrných "hyperkomplexních čísel" bušili horem dolem. Mezi nimi zaujímal čestné postavení irský fyzik a matematik William Rowan Hamilton.
Ten si jednoho dne uvědomil, že nemá smysl v 3D prostoru hledat reálnou jedničku (tedy vektor splňující "jedna krát cokoliv je to samé"). Celý 3D prostor je nutno udělat imaginární a jednička bude žít v další dimenzi mimo něj. Takže zlomil hůl nad hledáním komplexních čísel v 3D a začal experimentovat s 4D, kde se mu posléze podařilo definovat kýžené rozšíření v podobě kvaternionů, které se na jeho počest značí písmenkem H (kvéčko je v matematice rezervováno pro racionální čísla). Kvaternion q tedy můžeme zapsat buď jako 4D bod (tedy čtveřici reálných čísel) a nebo pomocí nezávislých "imaginárních jednotek" i, j a k:
q = {a,b,c,d} = a+bi+cj+dk
Nejlepší je si ty "imaginární jednotky" představit jako jednotkové vektory ve směru souřadných os x, y a z, s tím, že b, c,a d udávají souřadnice obecného 3D vektoru vzhledem k těmto osám (skalár a reprezentuje reálnou složku kvaternionu). Jednou z možných reprezentací kvaternionu, se kterou se navíc dobře počítá, je proto dvojice skalár-vektor: (a,A) = (a,{b,c,d}).
Sčítání kvaternionů je jednoduché a probíhá - jak jinak - po složkách. Tedy podle osvědčeného principu "svůj k svému":
(3+2i-j-2k) + (1+0i+2j+k) = 4+2i+j-k
Potíže nastávají se součinem. Abychom mohli takové příšerky násobit, musíme si v první řadě říci, jak spolu násobit ty 3 imaginární jednotky i, j a k, které okupují 3 různé souřadné osy. Klíčem k úspěchu je zde rovnice:
i * j = k
Z ní (a z rovnic popisujících imaginární jednotky: i2 = j2 = k2 = -1) se dá odvodit vše ostatní. Musíme to ovšem udělat opatrně, protože se nedá apriori očekávat, že tyto podivné jednotky budou komutovat. Nejprve tu rovnici vynásobíme zleva íčkem a dostaneme (s využitím i2 = -1)
i*i*j = -j = i*k
tuto druhou rovnici vynásobíme zprava káčkem (a opět použijeme k2 = -1)
-j*k = i*k*k = -i a tedy i = j*k
no a tu poslední rovnici vynásobíme zleva jéčkem (j2 = -1) a dostaneme
j*i = j*j*k = -k
A malý průšvih je na světě. To j*i je skutečně něco jiného než i*j a v důsledku toho musíme při počítání dbát velmi pečlivě na pořadí součinitelů. Kvaterniony (na rozdíl od komplexních čísel) nejsou komutativní!
Když to shrnu, tak pro ty tři jednotky platí následující vztahy:
i*j = k = -j*i
j*k = i = -k*j
k*i = j = -i*k
(nejlepší způsob jak si je pamatovat je představit si vektorový součin souřadnicových jednotkových vektorů i,j,k)
Jakmile spolu umíme násobit tyto "imaginární jednotky", máme vyhráno. Obecné kvaterniony se roznásobí jako mnohočleny (a připravte se na to, že uvidíte hafo členů) a všechny součiny jednotek se upraví podle výše uvedených vztahů.
Kdo se nebojí, může si to zkusit:
(3+2i-j+2k) * (-1+2i+0j+k) = ... uff ... = -9 + 3i + 3j + 3k
Kdo nerad přemýšlí a raději má explicitní vzorečky do kterých se dá dosadit, může si spočítat součin dvou obecných kvaternionů takto (a aby se mi íčka, jéčka a káčka nepletla pod nohy, rozepíšu to ve formě bodů s indexovanými proměnnými)
{x0,x1,x2,x3} . {y0,y1,y2,y3} = {x0*y0-x1*y1-x2*y2-x3*y3,x0*y1+x1*y0+x2*y3-x3*y2, x0*y2-x1*y3+x2*y0+x3*y1, x0*y3+x1*y2-x2*y1+x3*y0}
(pochopitelně nedoporučuji takovou ohavnost počítat v ruce - nejlepší je si podle toho vzorečku naprogramovat počítač)
Můžete si ale zkusit, že když si vezmete kvaternion, který reprezentuje jedničku, tedy {1,0,0,0}, a pronásobíte s ním libovolný obecný kvaternion {a,b,c,d}, tak výsledkem bude opět ten samý kvaternion (to se pane nasmějete!)
+++++++++
Další možností jak si kvaterniony představit jsou komplexní čísla složená z komplexních čísel - tedy něco co má tvar a+bj, kde a a b jsou komplexní čísla a j je "další" imaginární jednotka (kterou jsem si označil j, aby se nepletla s imaginární jednotkou i, schovanou v těch komplexních číslech). To potom kvaternion vypadá například takto (a opět si ho můžeme představit jako pár a nebo v algebraickém zápisu):
q = {2+3i,1+2i} = (2+3i) + (1+2i)j
Po roznásobení si to závěrečné ij pro jednoduchost označíme jako k (abychom to ij nemuseli pořád tahat s sebou) a máme v podstatě zpět originální vyjádření kvaternionu. Výhodou tohoto zápisu je, že kvaternionové násobení dostane v podobě komplexních dvojic jakž takž snesitelnou podobu (* značí číslo komplexně sdružené):
{w1 , w2} . {z1 , z2} = {z1.w1 - z2.w2* , z1.w2+z2.w1*}
(všimněte si, že kdybych vám neřekl, že ta čísla napravo jsou komplexní - a tedy kdyby tam nebyla ta sdružovací hvězdička - tak by to vypadalo jako úplně normální definice komplexního součinu - a to je podstatně jednodušší záležitost než ta 4D součinová hrůza citovaná nahoře).
A dáme si komplexní příklad (nezapomeňte na ta sdružená čísla na konci formulky):
{2+3i,1+2i} . {1+5i,-3-4i} = {-2+15i,17-20i}
No a kdo si troufá, může si totéž spočítat přes klasický kvaternion:
(2+3i+j+2k).(1+5i-3j-4k) = (-2+15i+17j-20k)
Další výhodou tohoto zápisu je, že se nemusíte trápit s 4D prostorem. Pokud umíte dobře počítat s komplexními čísly, tak je vymalováno. Mimochodem, kdo umí dobře kvantovou fyziku, může si kvaterniony představit také jako Pauliho matice - tyto dvě struktury jsou algebraicky ekvivalentní).
+++++++++
Jak jsem se zmínil na začátku, kvaternion se dá reprezentovat jako pár skalár-vektor. Symbolicky zapsáno: (v,V), kde v je reálné číslo a V je reálný 3D vektor, tedy trojice čísel V = {v1, v2, v3}. Místo žonglování s íčky, jéčky a káčky pak žonglujete jenom s běžnými skaláry a 3D vektory.
Takže místo kvaternionu q = 2+4i+3j+k dostanete vyjádření q = (2,{4,3,1})
Sčítání je zase jednoduché - prostě sečtete skaláry a vektory zvlášť. Důležité je, že i pro násobení dostanete poměrně snesitelnou formulku:
(v,V) * (w,W) = (vw - V.W, vW + wV + VxW)
kde V.W je skalární součin vektorů a VxW jejich vektorový součin.
Zda si kvaterniony představujete jako čtveřice reálných čísel, dvojice komplexních čísel, páry skalár-vektor a nebo Pauliho matice je jen a jen na vás.
++++
Většina učebnic ale používá první způsob, takže se vrátíme k algebraickému zápisu.
q = a + bi + cj + dk
Podobně jako u komplexních čísel definujeme sdružený kvaternion formulkou
q* = a - bi - ci - dk
(reálnou složku necháme jak je a u všech imaginárních prohodíme znaménko)
a délku neboli absolutní hodnotu kvaternionu pak spočítáme - stejně jako u komplexních či hyperbolických čísel - podle vzorečku
|q|2 = q . q*
což po vyčíslení vede k definici
|q|2 = a2+b2+c2+d2
Kvaterniony, které mají jednotkovou délku se jmenují jednotkové (to jste nečekali, co?) a tvoří teoretickou základnu pro počítání s trojrozměrnými rotacemi. Ekvivalentem čistě imaginárních komplexních čísel (tedy takových jejichž reálná část je nula - např. 5i) je tzv. "ryzí kvaternion" (pure quaternion), který má nulovou reálnou složku. Odpovídá tedy zápisu bi+cj+dk a nebo páru skalár-vektor (0,V), takže se na něj můžeme de facto dívat jako na 3D vektor.
+++++++++
Z pohledu fyzika vypadá kvaternion tak trochu jako časoprostorový vektor. Má 3 prostorové souřadnice a pak jednu, která je "trochu jiná". Takže si tu reálnou složku klidně můžete představit jako čas a dostanete "čtyřvektor" {t,x,y,z}. Ovšem hlubším aplikacím kvaternionů ve speciální relativitě brání to, že jejich délka je součet čtverců všech souřadnic (t2+x2+y2+z2), což neodpovídá tomu, jak měříme délku v Minkowského prostoročasu (-t2+x2+y2+z2). Pokud jste ale četli sekci Jauvajs, tak si možná řeknete, že tato nevýhoda by se dala odstranit tím, že bychom některou z těch imaginárních jednotek nahradili hyperbolickou jednotkou. Koneckonců, Lorentzova transormace je v zásadě hyperbolická rotace.
Jenže jakmile vypustíme hyperbolického džina z lahve, tedy umožníme některým jednotkám chovat se hyperbolicky, dostaneme spoustu dalších algebraických struktur. Zde se zmíním pouze o dvou.
Hyperbolické kvaterniony dostaneme pokud ty tři imaginární jednotky nahradíme jejich hyperbolickými ekvivalenty ze sekce Jauvajs: i2 = j2 = k2 = +1. Tady už pro délku (absolutní hodnotu) kvaternionu q = a + bi + cj + dk dostaneme poměrně nadějný výraz q.q*=a2-b2-c2-d2, ale tyto kvaterniony nejen, že nejsou komutativní, ale na rozdíl od těch Hamiltonových nejsou ani asociativní. Není mi známo, zda se někomu s jejich pomocí podařilo sestrojit funkční model prostoročasu, který by dokázal něčím podstatným přispět ke stávající teorii.
Nakonec Vám představím své nejmilejší kvaterniony, které kombinují ty Hamiltonovy s těmi hyperbolickými. V angličtině se jim říká split quaternions a čtverce jejich jednotek splňují: i2 = -1, j2 = 1, k2 = 1. Jejich absolutní hodnota se dá odvodit z výrazu q.q*=a2+b2-c2-d2 a tak jako Hamiltonovy kvaterniony popisují 3D rotace (viz další sekce), tyto kvaterniony popisují isometrie na rotačním hyperboloidu. No nekupte to!
Literární shrnutí této sekce: Za sedmero horami a sedmero řekami žil čaroděj Algebrus a ten si jednou z dlouhé chvíle uplácal z opotřebovaných komplexních jednotek synka Kvaternionka. Synek rostl jako z vody a zanedlouho začal lumpačit - tu svému tatínkovi schoval obor integrity za kredenc, tu mu snědl Dedekindovy řezy a jednou mu dokonce utáhl inverzní matici tak silně, že nešla povolit ani francouzským klíčem. A to už se Algebrus vytočil, popadl čarodějnou hůlku a milého Kvaternionka proměnil v bůžka otáčení.
+++++++++
3D rotace
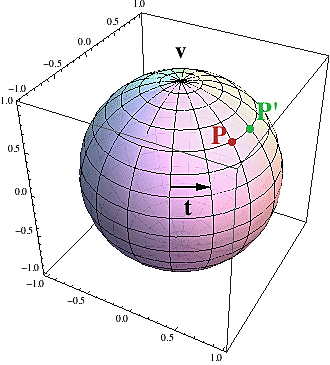
Na začátku jsme si řekli, že abychom pochopili 2D rotaci, stačí pochopit co se děje na jednotkové kružnici. S 3D rotací je to podobné. K tomu, abychom ji dokázali popsat bohatě stačí, když ji zadefinujeme na jednotkové sféře (tedy kouli). Jakmile umíme zarotovat se sférou, všechny ostatní body v prostoru se otočí pomocí triku popsaného v úvodu.
Sféru si představte jako zeměpisný globus. Jsou dva způsoby, jak s ním otočit. Pokud je osa otáčení shodná se zemskou osou (tj. severní pól - jižní pól), zatočíme s ním jednoduše tak, že do globusu lehce ťukneme prstem a ejhle - už se točí. Daleko těžší je otočit globusem kolem nějaké obecné osy, např. kolem osy procházející Prahou (a jejím protilehlým bodem). V tomto případě musíme nejprve sundat globus ze staré osy, vyvrtat v něm dírky a pak jimi provléknout novou osu, kolem které se globus bude moci otáčet.
S matematickým popisem 3D rotace je to obdobné. Pokud budete chtít sférou otočit o daný úhel kolem jedné ze souřadných os, dá se to poměrně lehce popsat rotačními maticemi, které nejsou v tomto případě o moc komplikovanější než jejich 2D protějšky. Každý bod na sféře odpovídá 3D vektoru P a jeho obraz po otočení o úhel t se spočítá jako součin příslušné rotační matice R(t) a tohoto vektoru:
P' = R(t).P
Větší problém nastane, pokud si na sféře vybereme nějaký obecný bod, a zase si ho představíme jako jednotkový vektor, řekněme V = {1/9, 4/9, 8/9}, a budeme se snažit otočit celou sféru o daný úhel t kolem této osy.
I v tomto případě se ta rotační matice dá najít, ovšem je to po všech čertech komplikovaný výpočet. Navíc ve finálním tvaru té matice není osa otáčení vidět explicitně (ta se z ní musí vyždímat pomocí tzv. vlastních vektorů).
+++++++++
Kvaterniony jsou pro 3D rotace mimořádně dobře uzpůsobeny, protože v sobě obsahují jeden skalár (ten použijeme k určení úhlu) a jeden 3D vektor (osa otáčení). Budeme ovšem používat pouze jednotkové kvaterniony (tak jako 2D rotace používá pouze jednotková komplexní čísla).
Dá se ukázat, že každý jednotkový kvaternion se dá zapsat ve speciálním tvaru (trochu připomínajícím formát skalár-vektor):
r(t,V) = cos(t/2) + sin(t/2) V
kde první člen za rovnítkem je reálná část kvaternionu a ten zbytek je jednotkový 3D vektor V = xi+yj+zk pronásobený číslem sin(t/2). Takovému kvaternionu říkáme rotační, protože bude reprezentovat rotaci sféry o úhel t (nikoliv t/2 jak by se mohlo zdát!) kolem osy určené jednotkovým vektorem V.
Pro daný jednotkový kvaternion není těžké ten úhel t i osu otáčení V spočítat. Tady jeden jednotkový máte:
q = {0.140028, 0.70014, -0.420084, -0.560112}
První složka se musí rovnat cos(t/2), takže z toho dostaneme t = 2.86061 (radiánů). Toto bude úhel otočení. Sínus poloviny tohoto úhlu je sin(t/2)=0.990148. Tímto číslem vydělíme poslední tři souřadnice kvaternionu q a dostaneme jednotkový 3D vektor V = {0.707107, -0.424264, -0.565685}. Ten definuje osu otáčení. Takže pro q dostaneme zhruba rotační zápis:
q = cos(2.86/2) + sin(2.86/2) {0.707,0.424, 0.565}.
Všimněte, že definice rotačního kvaternionu r(t,V) je formálně příbuzná zápisu jednotkového komplexního (či hyperbolického) čísla pomocí výše zmíněné Eulerovy formulky (jen je v něm místo íčka vektor V - tedy kombinace i, j, a k). Proto se rotační kvaterniony poměrně dobře pamatují. Jedinou podivností je, že se v nich vyskytuje jen poloviční úhel, což často způsobuje bouři zmatení v hlavách studentů (viz zde a nebo zde).
Tato záhada je v podstatě způsobena nekomutativností kvaternionů. Zatímco u komplexních čísel je jedno, zda na ně připlácneme exponencielu zprava nebo zleva, u kvaternionů to jedno není, a proto ten rotační kvaternion uvidíme ve výsledné formulce dvakrát - jednou aplikovaný zprava a jednou zleva. Je to jako když řemeslníkovi řeknete "půlku vám dám teď a půlku po provedení práce" :-)
+++++++++
Kvaterniony ale neumí násobit body na sféře, takže my ten bod P, se kterým se chystáme nesmlouvavě zatočit, budeme muset nejprve proměnit v kvaternion. A jelikož bod P na sféře je jednotkový vektor, proměníme ho v ryzí kvaternion (jednotkové délky):
p = (0,P)
No a teď už je to brnkačka. Obraz bodu P po rotaci o úhel t si označíme jako P' (viz obrázek nahoře) a pro jeho reprezentaci ryzím kvaternionem p' platí celkem jednoduchá rotační formulka:
p' = r(t,V) * p * r(-t,V)
kde * je násobení příslušných kvaternionů (a ano, napravo je mínus t).
Tato formulka připomíná komplexní 2D rotaci. Tam jsme komplexní číslo z vynásobili komplexní jednotkou. Zde vynásobíme ryzí kvaternion p z každé strany rotačním jednotkovým kvaternionem (který v sobě obsahuje polovinu žádaného úhlu) a dostaneme ryzí kvaternion p', který v sobě nese souřadnice pootočeného bodu P'. Navíc má tento zápis prostřednictvím rotačních kvaternionů tu báječnou vlastnost, že osa otáčení i úhel se z nich dají poměrně jednoduše vydundat (jak jsem ukázal v příkladu nahoře).
Mimochodem, 3D rotace kolem počátku jsou - na rozdíl od těch 2D - nekomutativní (záleží u nich na pořadí!). Takže nás nepřekvapí, že jejich popis musí na svá bedra vzít nekomutativní kvaterniony, zatímco v 2D si vystačíme s komutativními komplexními čísly. Vše o čem se bavíme je vlastně jen násobení, ale tak jak popisujeme komplikovanější a komplikovanější procesy, musíme násobit komplikovanější a komplikovanější algebraické objekty (uvědomte si třeba, že v 3D rotují body na rovníku úplně jinak než body poblíž pólu - to se musí v té struktuře nějak odrazit).
+++++++++
Příklad A: jednoduchý
Otočíme bod P = {3/5,4/5,0} podél osy z o 60°.
Osa otáčení tedy bude V = {0,0,1}. Toto je tím páem v podstatě 2D rotace uvnitř roviny x-y a můžete si ji spočítat i bez kvaternionů. Stačí si vyčíslit tento komplexní výraz (60° je v radiánech 1.0472):
exp(1.0472 i)*(.6 + .8i) = -0.39282 + 0.919615 i
S nimi to proběhne takto. Rotační kvaterniony budou
r = r(60°,V) = cos(30°) + sin(30°) V = .8666 + 0.5 {0,0,1} = 0.866+0i+0j+0.5k
rr = r(-60°,V) = cos(30°) - sin(30°) V = .8666 - 0.5 {0,0,1} = 0.866-0i-0j-0.5k
(když si sečtete čtverce těch 4 komponent, tak skutečně dostanete jedničku, takže je to pravý ořechový jednotkový kvaternion)
Náš bodík P se promění v ryzí kvaternion p = 0 + 0.6i + 0.8j + 0k
No a teď už je to jen otázka provedení dvou kvaternionových násobení:
p' = r * p * rr
Uděláme to ve dvou krocích (a bacha na pořadí!):
q = r * p = 0.+ 0.119615i+ 0.99282j+ 0k
p' = q * rr = 0-0.39282i+0.919615j+0k
Ten závěrečný p' je opět čistý kvaternion a odpovídá bodu na sféře P'={-0.39282,0.919615,0} a to je prakticky ten samý bod, který nám na začátku příkladu vyšel z komplexní rotace (mimochodem, pokud vám p' nevyjde jako ryzí kvaternion, máte někde chybku).
+++++++++
Příklad B: složitější
Teď si za osu otáčení zvolíme obecný bod na sféře V = {1/9, 4/9, 8/9} - tedy přesněji přímku procházející počátkem a tímto bodem - a naším úkolem bude otočit sférický bod P = {18/35,1/35,30/35} kolem osy V o úhel 50°.
Takže hlavní aktéři naší kvaternionické orgie budou následující:
(a zde ty kvaterniony napíšu jako 4D body)
p = {0.,0.514286,0.0285714,0.857143}
r = r(50°,V) = cos(25°) + sin(25°) V = {0.906308, 0.0469576, 0.18783, 0.375661}
rr = r(-50°,V) = cos(25°) - sin(25°) V = {0.906308, -0.0469576, -0.18783, -0.375661}
no a zbytek proběhne opět ve 2 krocích
q = r * p = {-0.351511, 0.616365, 0.178842, 0.681578}
p' = q * rr = {0., 0.63596, 0.427649, 0.642395}
p' je opět ryzí kvaternion a odpovídá otočenému bodu P' = {0.63596, 0.427649, 0.642395}
+++++++++
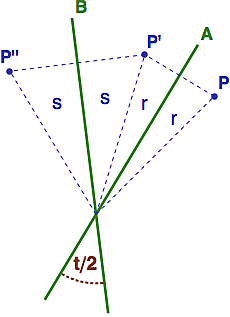
Závěrem ještě jednu poznámku k tomu, proč má ten rotační kvaternion v definici jen poloviční úhel (to vysvětlení nahoře je trošičku "fake"). Odvození rotačního vzorečku je poměrně komplikované (najdete ho např. v níže citované Needhamově knížce na str. 288), nicméně v principu je založeno na jednom geometrickém faktu, který si zaslouží pozornost sám o sobě.
Rotace o úhel t odpovídá složení dvou zrcadlení v přímkách A a B, které se protínají pod úhlem t/2. To je ta skulinka, kterou se do vzorečku pro rotační kvaternion odpovídající úhlu t dostane poloviční úhel t/2 (a stejně to funguje pro dvě přímky ve sférické geometrii).
Důkaz není obtížný a v podstatě se dá vykoukat z obrázku napravo. Zrcadlení obou přímek postupně přesune bod P do bodu P' a nakonec P'' a při tom zachovává úhly r a s (a vzdálenosti těchto bodů od průsečíku se samozřejmě nemění - to je vlastnost zrcadlení). Když si to všechno sečtete, dostanete, že úhel rotace P na P'' je roven r+r+s+s, zatímco úhel mezi oběma přímkami je r+s. Takže je-li úhel mezi přímkami t/2, úhel rotace bude dvojnásobkem, čili t.
+++++++++
Koho zajímají výhody a nevýhody použití kvaternionů v počítačové grafice nebo hrách, může dále nahlédnout sem:
Understanding QuaternionsDo we really need quaternions?Rotating Objects Using Quaternions
Tímto se loučíme s pozoruhodným světem imaginárních jednotek a příště se navrátíme do světa reálného. Pokud chcete proniknout hlouběji do tajů komplexních čísel - včetně aplikací v neeukleidovských geometriích - vřele doporučuji knihu Tristana Needhama: Visual Complex Analysis.
+++++++++
Tady končí komplexní minisérie a to znamená, že nás čeka co? Správně. Písemná zkouška. Takže se netěšte na žádné uvolňování a hezky si vytáhněte propisky a indexy. Combo FH: Když nám teče do bot.
Předchozí díly Matykání.
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
| Další články autora |
Tři roky vězení. Soud Ferimu potvrdil trest za znásilnění, odvolání zamítl
Městský soud v Praze potvrdil tříletý trest bývalému poslanci Dominiku Ferimu. Za znásilnění a...
Studentky rozrušila přednáška psycholožky, tři dívky skončily v nemocnici
Na kutnohorské střední škole zasahovali záchranáři kvůli skupině rozrušených studentek. Dívky...
Takhle se mě dotýkal jen gynekolog. Fanynky PSG si stěžují na obtěžování
Mnoho žen si po úterním fotbalovém utkání mezi PSG a Barcelonou postěžovalo na obtěžování ze strany...
Školu neznaly, myly se v potoce. Živořící děti v Hluboké vysvobodili až strážníci
Otřesný případ odhalili strážníci z Hluboké nad Vltavou na Českobudějovicku. Při jedné z kontrol...
Prezident Petr Pavel se zranil v obličeji při střelbě ve zbrojovce
Prezident Petr Pavel se při střelbě na střelnici v uherskobrodské České zbrojovce, kam zavítal...
„Smrt režimu.“ Za nápis si má nezletilá ruská studentka odpykat 3,5 roku
Ruský vojenský soud odsoudil žákyni desáté třídy, sedmnáctiletou Ljubov Lizunovovou ke 3,5 roku...
Zavolíme! Kandidáti do eurovoleb se utkají v debatě vysílané i studentům škol
Šest kandidátů pro volby do Evropského parlamentu přijalo účast v debatě Zavolíme!, která bude...
Další případ zpožděné dodávky zbraní. Česká firma se soudí na Ukrajině
Premium Vztahy mezi Českem a Ukrajinou nejsou vždycky idylické. Svědčí o tom soudní spor, na který narazila...
Světlušky mění válčení ve městech. Nové drony snížily počet padlých Izraelců
Premium Jen několik decimetrů velký přístroj může znamenat revoluci městské války: minivrtulník, který...
- Počet článků 402
- Celková karma 19,54
- Průměrná čtenost 920x