Matykání: na Den matek z matic zmatek
(domácí úkol: jaká je zdrobnělina slov "matematik" a "matematička"?)
A teď už vážně.
Mnoho věcí na této planetě má duální charakter. Tedy můžeme na ně nazírat dvěma (a někdy i více) různými způsoby a tento dvojí náhled nám zpravidla podá plastičtější obraz reality než pohled z jednoho jediného úhlu.
Představte si třeba ředitele velké továrny, pana Josefa Dubského, který je současně dědečkem. Obě role mají specifické vzorce chování a pokud byste se vnučky zeptali na dědu Pepu, obdrželi byste asi úplně jiné ohodnocení než jaké by pan šéf dostal od řadového zaměstance. A přestože jsou oba náhledy na první pohled diametrálně odlišné, skrývá se za nimi jedna a ta samá osoba. V mnoha případech nám její chování v roli "ředitel" umožní pochopit některé odstíny role "dědeček" a naopak.
Takovýmto způsobem se třeba kvantová fyzika dívá na fotony - neúnavné to šiřitele světla. Pro určité typy úvah je přirozené se na ně dívat jako na elementární částice, zatímco pro jiné je výhodnější pohlížet na fotony jako na vlny. Oba úhly pohledu obohacují naše porozumění a pomáhají nám vytvořit si o mikrosvětě dostatečně přesný obraz.
I v matematice existují objekty na které můžeme pohlížet dvěma různými způsoby a jejich duální zvládnutí nám umožní objekt lépe zasadit do našeho vnitřního myšlenkového světa. Každý máme ta chápací kolečka nastavená jinak. Někdo potřebuje objekty svého poznání vidět a preferuje geometrický náhled, někdo umí s objekty zručně manipulovat a preferuje náhled algebraický.
Jedním z takových obojetných objektů je matice. V zásadě je to uspořádaná rota čísel, která pochoduje po algebraickém buzerplacu v pevně sešikované formaci, připravená ztéci zdrcujícím útokem zákopy lineárních rovnic. V algebraickém náhledu ta čísla prostě reprezentují nějaké proměnné a vztahy mezi nimi. Můžeme na ně ale pohlížet i méně tradičně - geometricky - jako na speciální typ zobrazení (funkce) mezi dvěma vektorovými prostory. Každý si může vybrat to primární hledisko, které mu více vyhovuje.
Dnes začnu krátkým zopakováním algebraických vlastností a pak se vrhneme do zkoumání geometrie příslušných zobrazení (v kontextu vektorových prostorů se funkcím a zobrazením také často říká transformace anebo operátory).
+++++++++
Maticové opáčko
Na té nejelementárnější úrovni matice představují obdélníkové schéma čísel, obvykle sevřené v závorkách, které vidíte na obrázku vpravo. Matice A rozměru mxn mají m řádků a n sloupců. Pokud ty řádky a sloupce prohodíte, dostanete tzv. matici transponovanou A?, která má řádků n a sloupců m.
Na trochu sofistikovanější úrovni si matici A můžete představit buď jako 2 řádkové vektory (z R3) nebo 3 sloupcové vektory (z R2). Oba náhledy mají v aplikacích své uplatnění.
Já budu matice popisovat jako kolekce řádkových vektorů - takže v textu ta matice A z obrázku bude vypadat takto:
A = ((1,2,3),(0,-1,1))
Číslo v i-tém řádku a j-tém sloupci matice A značíme A(i,j) a často pro ty indexové proměnné i,j používáme subscript.
Než se začneme vrtat v násobení, rád bych se zmínil o jednom notačním problému. To, zda A(i,j) označuje element v i-tém řádku a j-tém sloupci nebo naopak v i-tém sloupci a j-tém řádku je věci konvence. Stejně jako ježdění vpravo nebo vlevo (obojí je možné, ale historie si u nás vybrala tu první možnost). Bohužel v případě matic se ta první (a všeobecně akceptovaná) konvence dostala do sporu s fungováním počítačové grafiky. V 2D geometrii je každý obrázek reprezentován maticí pixelů M(i,j). To znamená, že když měníme první index (i), v obrázku se pohybujeme svisle, zatímco druhý index (j) nás posunuje ve směru vodorovném. To je v rozporu se standardní definicí souřadnic (x,y), kde první složka (x) nás posunuje vodorovně a druhá (y) svisle. Digitální verze pak vede jednak ke zmatení studentů a druhak k nutnosti různých převodových formulek v počítačových programech. A tak mne často napadá, zda by se lineární algebra neměla přizpůsobit a změnit tu (i,j) konvenci tak, aby byla kompatibilní s geometrií obrázku, tj. aby první "souřadnice" udávala sloupec (tedy polohu na ose x). Zadarmo by to ale nebylo. Musela by se přeznačit celá lineární algebra. Všechny knihy, učebnice, články a mozkové závity lineárních algebraiků.
+++++++++
Matice lze za určitých okolností násobit mezi sebou.
Máme-li matice A typu mxk a matici B typu kxn, pak jejich součinem je matice C=A.B typu mxn, která je definovaná takto: matici A rozřežeme na řádky, matici B na sloupce a element C(i,j) je pak skalární součin i-tého řádku A a j-tého sloupce B.
V aplikacích se nejčastěji setkáme s případem, kdy matice A i B jsou čtvercové (a stejného typu nxn). V tomto případě se na násobení matic můžete dívat jako na určitý pokus emulovat násobení čísel. A jisté paralely zde skutečně jsou.
Roli jedničky hraje jednotková matice, která má všude nuly, jen na hlavní diagonále - tedy na pozicích (i,i) - má jedničky. Značí se písmenkem I a splňuje přesně to, co od "jedničky" očekáváme:
A.I = A = I.A
Pokud se k dané matici A dá najít matice B tak, že A.B = I pak říkáme (opět v analogii s čísly), že A je invertovatelná a matice B je její inverzní matice. Ta se značí A?1 a je jakousi obdobou převrácené hodnoty. Platí pro ni:
A.A?1 = A?1.A = I
Matice můžeme také sčítat a násobit skalárem (obě operace jsou přirozeně definovány na úrovni prvků), takže se na ně můžeme dívat jako na vektorový prostor. Díky tomu, že ty čtvercové se dají rozumně násobit i mezi sebou, představují o něco bohatější strukturu, které se říká "algebra" (pozor, neplést s názvem celé disciplíny).
Ta analogie s čísly ale samozřejmě není perfektní. Násobení matic je sice asociativní i distributivní
A.(B.C) = (A.B).C
A.(B+C) = A.B + A.C
(A+B).C = A.C + B.C
ale není komutativní
A.B ? B.A
takže si musíme dávat pozor v jakém pořadí matice násobíme.
Např. pro matice nahoře dostaneme
A.A? = ((14,1),(1,2))
A?.A = ((1,2,3),{2,5,5),(3,5,10))
Vidíte, že výsledkem jsou dokonce matice různých typů.
Komplexní čísla jsou sice o něco zdařilejším pokusem o zobecnění násobení reálných čísel, ale ta zase fungují pouze v dimenzi 2 (popřípadě 4 pokud vezmeme na milost kvaterniony). Čtvercové matice se dají násobit pro libovolný typ nxn.
+++++++++
Sekce Jauvajs: Dualita
(tuto motivační sekci můžete přeskočit)
Abychom se na matice mohli podívat jako na zobrazení (tedy určitý typ funkce), rozebereme si důkladně situaci v jedné dimenzi.
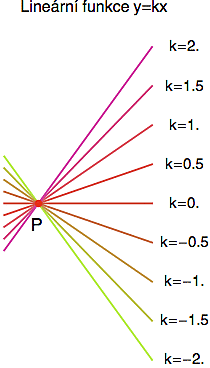
Každé reálné číslo k je de facto matice 1x1 - mohli bychom si ji označit jako (k). P, že každé reálné číslo k odpovídá lineární funkci f(x)=kx (viz obrázek). A naopak, každou lineární funkci z R do R (tedy přímku procházející počátkem) můžeme jednoznačně reprezentovat její směrnicí k.
Zda si číslo k (matici 1x1) představujete jako algebraický objekt (něco co se dá sčítat a násobit) anebo objekt geometrický (funkce z R do R) je čistě na vás.
Tato přirozená dualita mezi čísly a lineárními funkcemi - a obecněji mezi vektory a funkcionály (jak jsme viděli před časem v sekci Jauvajs) - je fundamentální vlastností vektorových prostorů se skalárním součinem (při jeho absenci si funkcionály - čili kovektory - žijí svým vlastním životem v duálním prostoru). Podobně se i na matice můžeme dívat jako na zobrazení a z tohoto pohledu pak čerpat inspiraci pro další úvahy. Koneckonců všechno jsou to jen různé typy lineárních živočichů, kterým souhrnně říkáme tensory (čísla jsou tensory 0. řádu, vektory tensory 1. řádu a matice jsou tensory 2. řádu).
Zapřísáhlé praktiky ale musím uklidnit. Maticový počet lze s úspěchem aplikovat i bez palčivého hloubání o vektorech a kovektorech. Na transponovanou matici se můžete i nadále dívat jako na číselný obdélník, který někdo překlopil "na štorc". Jenom proto, že ta matice je ve skutečnosti zobrazením duálních prostorů, chleba nikde nezlevní. Pokud ale chcete lineární algebru dobře vstřebat, tak by se ten most mezi číslem řekněme 2.83 a lineární funkcí y=2.83x měl stát vaší druhou přirozeností.
+++++++++
Než se posuneme dál, ještě chci podtrhnout jednu maličkost.
Funkcí je obecně daleko více než čísel. To, že se nám podařilo vytvořit most mezi čísly a funkcemi na reálné ose (a za chvíli ho vytvoříme mezi maticemi a funkcemi na vektorovém prostoru) je umožněno tím, že jsme se omezili na velice speciální typ funkcí splňujících:
(L1) f(u+v) = f(u)+f(v)
(L2) f(a*u) = a*f(u)
Rigidita vzešlá z těchto vztahů bohatost funkčních prostorů dostatečně zkrotí. Lineární funkce navíc respektují oba hlavní nosné pilíře vektorových prostorů - sčítání a násobení skalárem - takže jsou s vektory přirozeně "skamaráděné". Takový postup je součástí obecnější filosofie.
Kdykoliv matematika objeví nějakou strukturu, tak se začne zajímat, zda neexistují nějaké funkce, které tuto strukturu zachovávají (v teorii grup jsou to třeba homomorfismy, které zachovávají grupovou operaci, v teorii variet zase homeomorfismy, které zachovávají topologické vlastnosti daného prostoru). A protože ve vektorovém prostoru dominuje lineární struktura - mezi funkcemi (zobrazeními) na tomto prostoru hrají prim ty lineární.
V každém případě nám tato zdánlivě samoúčelná abstrakce umožní klást si některé otázky, které by nás za normálních okolností nenapadly, a v konečném dopadu nás dovede k lepšímu pochopení mechaniky lineárních rovnic.
+++++++++
Matice jako zobrazení
V jedné dimenzi funguje dualita mezi čísly (tedy maticemi 1x1) a lineárními zobrazeními celkem zřejmým způsobem (y=k*x). Abychom ji mohli rozšířit do n-dimenzionálních prostorů, musíme se nejprve podívat jak lze danou matici A typu mxn pronásobit vektorem u z n-dimenzionálního prostoru U (abychom analogicky dostali v=A.u).
Pokud se na vektor u budeme dívat jako na sloupec matice typu nx1, je to vlastně speciální případ maticového součinu. Matici A nasekáme na řádky (jako v tom řádkovém značení) a pak každý řádkový vektor vynásobíme skalárně s daným vektorem u. Z této operace vyleze vektor v=A.u jehož dimenze bude rovná počtu řádků matice, tedy m.
Zobrazení f určené maticí A je nabíledni:
f(u)= A.u
Počet sloupců matice A vymezuje dimenzionalitu prostoru ze kterého zobrazujeme, zatímco počet řádků indikuje dimenzi prostoru do kterého zobrazujeme. Proto jsme se v minulé sekci na číslo a (což je matice 1x1) mohli dívat jako na lineární zobrazení z R1 do R1.
Příklad: výše uvedená matice A tedy reprezentuje zobrazeni z U=R3 do V=R2. Můžete si sami ověřit, jak funguje na konkretních vektorech:
A.(1,1,1) = (6,0)
+++++++++
To, že si z matice dokážeme ukuchtit lineární zobrazení asi nikoho nepřekvapí. Méně triviální je, že to platí i nazpátek - každé lineární zobrazení z prostoru U do prostoru V se dá reprezentovat vhodně zvolenou maticí (jejíž typ respektuje příslušné dimenze). Proto je tento geometrický náhled zcela univerzální.
Představme si, že máme lineární zobrazení f: R3->R2. Díky lineárním podmínkám L1 a L2 ze sekce Jauvajs je chování tohoto zobrazení plně určeno hodnotami na bázových vektorech (to je klíčový poznatek!). Obecný vektor u z R3 totiž rozepíšeme pomocí kanonické báze u=xi+yj+zk a jeho obraz v R2 pak lehce spočítáme
f(u) = f(xi+yj+zk) = x*f(i)+y*f(j)+z*f(k)
Když z těch tři vektorů vpravo (každý se dvěma složkami) uděláme sloupce matice A (která bude typu 2x3), dostaneme hledanou maticovou reprezentaci našeho lineárního zobrazení f.
f(u) = Au = A.(x,y,z)
Můžete si ověřit, že lineární zobrazení f(x,y,z)=(x+2y+3z,-y+z) z R3 do R2 se dá reprezentovat maticí A z úvodu. Sloupky této matice jsou přesně obrazy tří kanonických vektorů i,j,k.
(tato úvaha také naznačuje, proč se matice a vektory - a obecněji matice a matice - násobí takovým zvláštním způsobem. Násobení matic de facto vyjadřuje skládání příslušných zobrazení)
+++++++++
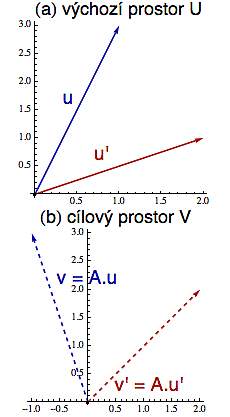
Protože zobrazení z mnohadimenzionálního prostoru U do mnohadimenzionálního prostoru V se těžko představují (už u komplexních funkcí jsme s tím měli trochu problémy), vypomůžeme si opět tím, že prostor U a V znázorníme odděleně.
Matice A typu mxn si tedy můžeme schematicky představit jako zobrazení f, které každému vektoru z n dimenzionálního prostoru U (obr a) přiřadí vektor z m dimenzionálního prostoru V (obr b). Ty dimenze vektorů musí přesně odpovídat rozměrům matice, jinak se příslušné skalární součiny zaseknou a definice nebude fungovat (stejně jako když se budete snažit strčit evropský spotřebič do americké zásuvky).
Mimochodem, není bez zajímavosti, že pokud se na komplexní čísla budeme dívat jako na vektory - tedy místo x+iy si představíme vektor (x,y), pak se komplexní násobení dá lehce "nafingovat" maticemi: vynásobení čísla x+iy číslem a+bi bude odpovídat vynásobení vektoru (x,y) maticí R = ((a,-b),(b,a)). To si lehce ověříte spočtením součinu R.(x,y) a pokud tomu budete chtít opravdu přijít na kloub, můžete si rozmyslet, že vydělením matice R dilatačním faktorem (a2+b2) dostanete de facto rotační matici (a komplexní násobení není - z pohledu transformací - nic jiného než složení dilatace a rotace).
+++++++++
Jinou možností jak si představit fungování lineárních zobrazení na vektorovém prostoru je vrátit se k naší původní představě funkce jako skříňky s trpaslíkem (vpravo).
Vhodíme do ní vektor z prostoru U, trpaslík ho popadne, vynásobí matici A tímto vektorem a výsledný vektor z prostoru V, tj. v=A.u, nám předhodí na výstupu.
Na procvičení si můžete rozmyslet, že definiční obor naší funkce f(u)=A.u bude celý prostor U, protože součin A.u lze provést pro libovolný vektor u (z prostoru U můžeme do trpaslíkovy skříňky vhodit cokoliv - a nemusíme se bát, že bychom dělili nulou nebo prováděli nějakou jinou nemístnou matematickou operaci).
Ale jak jsem poznamenal výše, je nutno dávat majzla, abychom dovnitř nevhazovali vektory jiné dimenze nebo dokonce kancelářské sponky, protože v tom případě by se trpaslík mohl zavařit (a zavařené trpaslíky si ke svíčkové dopřává pouze obr Koloděj).
Zvídavého čtenáře možná napadne, proč jsme v definici A.u matici A rozřezali na řádky a vynásobili vektorem zprava. Proč jsme ji nerozřezali na sloupce a nevynásobili zleva? To je opět věcí konvence, kterou můžeme přenechat koňovi. Masochisté se však mohou podívat na jemné rozdíly mezi řádkovými a sloupcovými vektory a zjistí, že zatímco ty sloupcové reprezentují vektory, ty řádkové reprezentují kovektory. No prosím, a jsme zase tam, kde jsme byli...
+++++++++
Podprostory
Podprostor je kus vektorového prostoru, který se sám o sobě chová jako vektorový prostor (tedy můžete v něm sčítat vektory a násobit skalárem aniž by vám hrozilo, že z toho prostoru vypadnete). Obvykle je to přímka či rovina procházející počátkem, občas i něco komplikovanějšího. Často je popsán jako lineární obal daných vektorů - tedy množina všech jejich lineárních kombinací. Např. pro dva nezávislé vektory u a v bude tento obal rovinou: w=a*u + b*v, kde a,b jsou libovolné skaláry. Ty dva parametry v ní nám naznačují, že máme co do činění s 2D útvarem.
Jak prostor U, tak prostor V, obsahují jeden zajímavý podprostor.
V případě výchozího prostoru U je to tzv. jádro matice A (neboli "nulový prostor"), které často značíme symbolem Ker(A) (z anglického "kernel"). Definuje se jako množina těch vektorů u, které se zobrazí na nulový vektor prostoru V
Ker(A) = {u?U, A.u=0}
To, že Ker(A) tvoří podprostor U si lehce ověříme (musíme ukázat, že z této množiny při tvorbě lineárních kombinací nevypadneme - srovnejte si to s pojmem uzavřenosti z tohoto Matykání). Pokud si vybereme dva vektory, u1 a u2, splňující A.u1=0 a A.u2=0 (oba vektory jsou tedy součástí jádra), pak jakákoliv lineární kombinace těchto vektorů u=a*u1+b*u2 bude díky rovnicím L1 a L2 splňovat A.u=a*A.u1+b*A.u2=0+0 a vektor u tedy bude také prvkem jádra.
A proč se s tím jádrem páráme? Protože spousta přirozených otázek se dá převést na jeho zkoumání. Např. kdy se dva vektory, u1 a u2 zobrazují maticí A do stejného vektoru? Tedy kdy platí A.u1 = A.u2? Z linearity zjistíme, že je to právě tehdy, když A.(u1-u2)=0 a to znamená, že rozdíl těchto vektorů musí být prvkem jádra matice A.
+++++++++
V cílovém prostoru V je oním zajímavým podprostorem množina všech obrazů zobrazení f - tedy něco co známe ze školy jako obor hodnot. Budu ji značit anglickým výrazem Range (volně přeloženo "rozsah").
Range(A) = {v?V, pro které existuje u?U: A.u=v)
V předchozí sekci jsme viděli, že je to v podstatě množina všech kombinací sloupcových vektorů, což jsou obrazy báze prostoru U. Protože každý vektor u se z té báze dá nakombinovat, jeho obraz se dá nakombinovat ze sloupců matice A (opět linearita). A z toho pak vyplývá, že Range(A) je podprostor.
Dimenzi tohoto podprostoru se říká hodnost matice A (některé matice to během svého života dotáhnou až na podplukovníka) a může být obecně nižší než dimenze cílového prostoru V. Představte si třeba bázi i=(1,0) a j=(0,1) prostoru U, kterou matice A=((1,2),(2,4)) zobrazí na kolineární vektory v 2D prostoru V. Range(A) je pak 1D přímka těmito vektory určená. Jádro Ker(A) zde bude 1D podprostor U určený vektorem (-2,1).
Studium obou těchto podprostorů (Ker(A) v prostoru U a Range(A) v prostoru V) je teoretickým podkladem pro studium řešitelnosti soustav lineárních rovnic (jak uvidíme příště). Kdo se pročetl až sem, získává ovšem již dnes čestný titul texaský ranger.
Literární intermezzo: Vzduch se chvěl jako mladá squaw před svatební nocí. Z vyprahlé krajiny trčely arizonské kaktusy jako němé vektory, ukazující ve zvlněné polopoušti směr gravitačního pole, pro případ, že by tu nějaký zoufalec chtěl vyhloubit studnu. Krvavý Džejk se nezúčastněně pohupoval v sedle upevněném koženými popruhy na hřbetě jeho věrného koně Pinta. Obhlížel trasu, kterou povedou železniční přípojku z měděného dolu k malé stanici v městečku Silver Creek. Za ním se ploužil jeho mladý pomocník Jim a co chvíli si přihnul z poloprázdné butylky. U vyschlého koryta potoka se oba zastavili a Džejk si s pohledem pevně vetknutým do mapy ověřoval detaily terénu. "Doufám, že jsi vzal dostatek čísel pro vyznačení kót a taky nějaké vektory k určení směru", utrousil dozadu. "Samozřejmě", durdil se Jim, "půjčil jsem si celý pytel čísel od farmáře Leibnitze a k tomu otýpku vektorů". Džejk nic neřekl, ale v duchu si pomyslel: "Zelenáč. Každý kovboj na západ od Mississippi ví, že v sedlové brašně má mít svoje vlastní čísla a svoje vlastní vektory."
+++++++++
Vlastní čísla a vlastní vektory
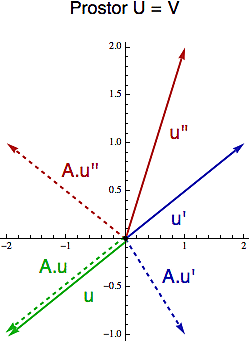
Pokud mají oba prostory U a V stejnou dimenzi - tedy matice A je čtvercová typu nxn - pak si můžeme tu mechaniku lineárního zobrazení představit v rámci jednoho obrázku (dole vpravo). Vezmeme si vektor u z našeho n-dimenzionálního prostoru U, vhodíme ho do trpaslíkovy skříňky a vypadne nám jiný vektor téhož prostoru, v=A.u, který si znázorníme přerušovanou šipkou. Na matici A pak můžeme nahlížet jako na transformaci, která popadne každý vektor a trochu s ním zacloumá (tu pootočí, tu protáhne, podle charakeru dané matice).
Protože vektory slouží - mimo jiné - k určení směru, nabízí se otázka, zda by se v tom prostoru U nenašel vektor u, takový, že jeho obraz při zobrazení v=A.u, leží v tom samém směru (to znamená, že matice ho jen trochu protáhne, ale nikam s ním zatáčet nebude).
Ptáme se tedy, zda pro danou matici A v prostoru U existují určité "kouzelné směry", které ta matice zachovává (na obrázku je jeden takový "kouzelný směr" vyznačen zeleným vektorem u)
Výpočetně vzato: pro danou matici A chceme najít vektor u, který se (touto maticí) zobrazí na svůj vlastní násobek (pro nějaký vhodně zvolený skalár ?)
(*) Au = ?u
Vektor splňující výše uvedenou rovnici se zove vlastní vektor matice A a příslušný skalár, který ukazuje stupeň prodloužení či zkrácení, vlastní číslo matice A (odpovídající vlastnímu vektoru u). Je-li vlastní číslo záporné, matice vektor současně obrátí do protisměru. V angličtině se těmto pokladům z kouzelného měšce říká "eigenvectors" a "eigenvalues". Souboru všech vlastních čísel (pro všechny možné vlastní vektory) říkáme spektrum matice A.
Spektrum matice je tedy množina skalárů, které ukazují jakým způsobem matice A "natahuje" ty "kouzelné směry" (je to vlastně jakási kolekce dilatačních koeficientů dané matice). Zajímavé je, že zatímco specifická forma vlastních vektorů závisí na volbě souřadnic (tj. na volbě bázových vektorů), vlastní čísla jsou vůči změně báze imunní. Proto patří k důležitým invariantům každé (čtvercové) matice.
Na tomto místě bych rád zdůraznil, že důležitý je skutečně pouze ten "kouzelný" směr, nikoliv specifický vektor u. Z rovnice (*) totiž celkem lehce vyplývá, že každý násobek vlastního vektoru je také vlastním vektorem. Např. A.(2*u) = 2*A.u = 2*(?u) = ?*(2u). Takže i dvojnásobek vektoru u splňuje rovnici (*). Pojem "vlastní vektor" je tedy tak trochu zavádějící. Výstižnější by bylo mluvit o "vlastním směru" anebo ještě lépe o vlastním podprostoru - protože občas se stane, že dva vlastní vektory sdílí stejné vlastní číslo a pak matice zachovává celý podprostor těmito vektory určený.
++++++
Čtenář-koumák si teď možná pomyslí, proč nedefinujeme vlastní vektory tak, že matice prostě zachová celý vektor (ne pouze jeho směr), což je samozřejmě o něco silnější vlastnost (hledali bychom vektory splňující rovnici Au=u). Ukázalo se, že taková vlastnost je příliš silná a jen velmi málo matic by pak mělo vlastní vektory. Zachování směru (namísto konkretního vektoru) je sice o něco slabší, ale všechny matice pak nějaký ten vlastní vektor mají. Spektrální analýza, která se tímto aspektem matic zabývá, patří díky tomu k nejúčinnějším nástrojům lineární algebry. Část kvantové mechaniky je dokonce vybudovaná na základech vlastních vektorů a jejich nekonečně rozměrných ekvivalentů - vlastních funkcí.
Čtenář-ještě-větší-koumák si ale vzpomene, že otočení v rovině o úhel ? se dá reprezentovat rotační maticí 2x2, která má tvar ((cos?, -sin?),(sin?,cos?)). Jak může mít matice, která celou rovinu (a tedy každý její vektor) otočí nějaký kouzelný směr, který zůstane zachován (tedy nepootočen)?
No, ono je to s těmi eigenpotvůrkami složitější. Občas se stane, že matice sice nemá žádné reálné vlastní číslo, ale má vlastní číslo, které je komplexní (a komplexní je pak i vlastní vektor). Ta rotace pak de facto vyplývá z vlastností komplexních čísel. U 3D rotací je to ještě komplikovanější, protože ty mají osu otáčení, která se zachovává přesně - takže příslušné rotační matice mají jedno reálné vlastní číslo ?=1 (a osa rotace je mu vlastním vektorem) a dvě komplexně sdružená, jejichž absolutní hodnota udává magnitudu rotace.
A těch zádrhelů je více. Například některá vlastní čísla (jak jsem výše naznačil) mají za vlastní vektor celý vícerozměrný podprostor. S takovými patologiemi si ale nebudeme lámat hlavu (každá učebnice lineární algebry vás tímto bludištěm ráda protáhne).
Prozatím se spokojíme s konstatováním, že matice nxn má typicky n vlastních čísel a vektorů, které jsou navzájem spárované, s tím, že občas mají vlastní čísla stejnou hodnotu a pak mohou ty vlastní vektory sdílet (kdo si rád hraje s technickými detaily, nechť se mrkne na Jordanovu normální formu matic).
Jak se ty "kouzelné směry" pro danou matici A spočítají si řekneme až přespříště. Nejprve se budeme muset naučit dělat s maticemi psí kusy.
+++++++++
Na světě je spousta typů krás. Precizně vycizelované okvětí orchideje skýtá zcela jiný prožitek než prostý půvab sedmikrásky. K tomu druhému typu řadím drobná klavírní dílka Edvarda Griega. Nejsou sice tak omračující jako Beethovenovy symfonie, ale odráží se v nich nejen nadpozemská krása norské přírody, ale i přímost a morální čistota obyčejného člověka, rvoucího se na dalekém severu o svou existenci. Pár z nich dosáhlo takové popularity, že jim Grieg vystřihl orchestrální podobu. Mým oblíbeným kouskem je norský tanec Gangar, jehož jednoduchá hudební schemata jakoby sbíhala z nekonečných horských plání k mámivému zrcadlu fjordu, aby se na jeho břehu oddala tanečnímu roji (původní klavírní verzi najdete zde). Edvard Grieg: Lyrická Suita (Gangar).
Předchozí díly Matykání
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
| Další články autora |
Tři roky vězení. Soud Ferimu potvrdil trest za znásilnění, odvolání zamítl
Městský soud v Praze potvrdil tříletý trest bývalému poslanci Dominiku Ferimu. Za znásilnění a...
Studentky rozrušila přednáška psycholožky, tři dívky skončily v nemocnici
Na kutnohorské střední škole zasahovali záchranáři kvůli skupině rozrušených studentek. Dívky...
Takhle se mě dotýkal jen gynekolog. Fanynky PSG si stěžují na obtěžování
Mnoho žen si po úterním fotbalovém utkání mezi PSG a Barcelonou postěžovalo na obtěžování ze strany...
Školu neznaly, myly se v potoce. Živořící děti v Hluboké vysvobodili až strážníci
Otřesný případ odhalili strážníci z Hluboké nad Vltavou na Českobudějovicku. Při jedné z kontrol...
Prezident Petr Pavel se zranil v obličeji při střelbě ve zbrojovce
Prezident Petr Pavel se při střelbě na střelnici v uherskobrodské České zbrojovce, kam zavítal...
Další případ zpožděné dodávky zbraní. Česká firma se soudí na Ukrajině
Premium Vztahy mezi Českem a Ukrajinou nejsou vždycky idylické. Svědčí o tom soudní spor, na který narazila...
Světlušky mění válčení ve městech. Nové drony snížily počet padlých Izraelců
Premium Jen několik decimetrů velký přístroj může znamenat revoluci městské války: minivrtulník, který...
Dva ruští vojáci se doznali k trojnásobné vraždě na Ukrajině
V okupované části Chersonské oblasti na jihovýchodu Ukrajiny zadrželi dva ruské vojáky, kteří se...
Architektonickou cenu EU získal univerzitní pavilon, blízko byla i ostravská galerie
Studijní pavilon Technické univerzity v německém Braunschweigu se stal vítězem prestižní...
- Počet článků 402
- Celková karma 19,54
- Průměrná čtenost 920x